
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf
Несмотря на некоторые отмеченные выше вопросы, в ЭТП, как представляется, скрыто еще очень много потенциальных возможностей. Одним из перспективных направлений работы, вероятно, является более глубокая проработка структуры уравнений ЭТП и входящих в нее основных понятий, придание им достаточно ясного физического смысла. Возможно, следует привнести в ЭТП идеи и подходы физической теории пластичности, изложению которой посвящена следующая глава.
Вопросы для самопроверки
1.Сопоставьте ОС истокообразной формы А.А. Ильюшина и ЭТП К. Валаниса. Какая форма является более общей и почему?
2.Какие известные эффекты пластического деформирования ЭТП описывает качественно удовлетворительно?
3.Приведите запись ОС ЭТП в «релаксационной форме», поясните механический и физический смысл входящих в ОС параметров.
4.В чем основная причина расхождения количественных результатов исходной формы ЭТП и экспериментальных данных?
5.Какие возможные варианты улучшения количественного соответствия теоретических результатов ЭТП и экспериментальных данных Вы знаете?
6.Приведите тензорно-параметрические ОС ЭТП в интегральной и дифференциальной формах. Что характеризует введенный вектор R?
7.Какие новые меры внутреннего времени были предложены А.Б. Мосоловым и К. Валанисом, в чем их основное отличие?
8.Какими недостатками обладает введенная К. Валанисом мера внутрен-
него времени (7.6) при = 1?
9. Поясните физический смысл параметра и вектора R, основываясь на статистическом подходе.
10.Какие параметры в предложенном К. Валанисом варианте ОС ЭТП можно отнести к внутренним переменным и почему?
11.Приведите физическое обоснование введения многоэлементных моделей ЭТП.
12.Запишите ОС ЭТП для конечного и бесконечного спектра внутреннего времени.
13.Каким образом в ОС ЭТП можно внести учет физического времени? Приведите возможные структурно-механические схемы многоэлементных ОС ЭТП, включающие временные эффекты.
14.Какие направления развития современной ЭТП Вам известны?
Натура тем паче всего удивительна, что в простоте своей многохитростна, и от малого числа
241
причин произносит неисчислимые образы свойств, перемен и явлений.
М.В. Ломоносов
8. О физической теории пластичности
Поиски «кирпичиков», «атомов», из которых можно было бы составить картину мироздания, никогда не прекращались в науке в целом. Механика и, в частности, теория пластичности не являются в этом смысле исключением. Параллельно с созданием и развит и- ем континуальных подходов в механике начиная с ХХ века инте н- сивно велись (и ведутся) работы по созданию теори й, основанных на рассмотрении глубинных физических механизмов деформир о- вания, присущих всем телам или их достаточно широким классам (например, металлам и сплавам). Сильнейшим импульсом для ра з- вития подобных теорий пластичности было открытие в 30 -х годах ХХ века дислокаций (см. гл.3), а вслед за этим – и других дефектов кристаллического строения материалов.
Под общим названием физической теории пластичности (ФТП) здесь будет пониматься широкий класс теорий пластичн о- сти, в основе формулировок определяющих соотношений, гипотез и основных положений которых лежит рассмотрение в явной форме механизмов деформирования на мезо- и микромасштабах
(т.е. масштабных уровнях, меньших уровня представительного объема в макросмысле, или представительного объема в инжене р- ном смысле), в силу чего материал данной главы существенным образом опирается и тесно связан с главой 3 (для облегчения работы с материалом часть необходимых соотношений и определений повторяется). Указанное обстоятельство составляет основное отличие ФТП от всех рассмотренных выше теорий пластичности (н а- зываемых в литературе по МДТТ обычно математическими те о- риями), в которых с самого начала формулировка теории осущес т- вляется в терминах континуальной механики, полей напряже ний, деформаций и других параметров.
Следует отметить, что возникновение и развитие физической теории пластичности как отдельной ветви теории пластичности неразрывно связано с пионерскими работами Дж. И. Тейлора, К.Ф. Элам [84, 85, 86] и Г.О. Закса [71]. С этого времени появилось огромное количество различных вариантов физических теорий, но практически во всех из них наблюдаются «родовые признаки» те о- рий указанных авторов, в особенности – Дж. И. Тейлора.
Установление масштабных уровней, вовлекаемых в рассм отрение в конкретном варианте ФТП, определяется требованиями исходной постановки задачи, особенностями исследуемых проце с- сов, известными сведениями или гипотетическими представлени я-
242

ми о лидирующих и аккомодационных процессах, определяющих неупругое деформирование. Решение вопроса о выборе уровней не лишено и субъективного компонента — квалификации исследователя, его приверженности тем или иным подходам, доступностью тех или иных инструментальных средств и т.д. В настоящее время
диапазон микромасштабов чрезв ычайно широк – от 10- 1 9 см3 до 10-
3 см3 .
Здесь будут рассмотрены соотношения ФТП только для моно -
иполикристаллических материалов (большей частью – металлов), однако подходы и некоторые гипотезы могут быть использованы при построении определяющих соотношений более широкого класса материалов. Более простыми объектами являются монокр и- сталлы, с описания поведения которых начинается построение практически всех вариантов физической теории пластичности.
Основным механизмом неупругого деформирования моно кристаллов в физической теории пластичности считается движение краевых дислокаций. Напомним (см. гл.3), что наряду с краевыми дислокациями в реальных моно - и поликристаллических телах наличествуют и винтовые дислокации, и множество других дефектов. То, что именно движущиеся дислокации являются основным и с- точником появления необратимых деформаций – факт, подтвержденный огромным количеством экспериментов. Включение в ра с- смотрение только краевых дислокаций обусловлено отчасти сл о- жившейся в ФТП традицией . Кроме того, как отмечалось в гл.3, винтовые дислокации имеют большую энергию активации и мен ь- шую плотность по сравнению с краевыми дислокациями.
Напомним, что краевая дислокация характеризуется своей плоскостью скольжения, положение которой будем определять единичной нормалью n, направленной в сторону экстраплоскости,
ивектором Бюргерса b, лежащим в плоскости залегания и хара к- теризующим несоответствие контуров, окружающих одиночную краевую дислокацию, и аналогичного контура в идеальном кр и- сталле; аналогично буд ет обозначаться единичный вектор в н а- правлении вектора Бюргерса (например, в определении ориентац и- онного тензора). Плоскости залегания и ориентация векторов Бю р-
герса, вдоль которых осуществляется трансляционное движение (скольжение) краевых дислокаций изве стны; ими являются наиболее плотно упакованные плоскости и направления. Так, в ГЦК - металлах скольжение краевых дислокаций осуществляется в пло с- костях системы 111 по направлениям 110 (иначе говоря, в системе скольжения {111}, <110>). В ОЦК – решетке трансляционное движение краевых дислокаций осуществляется в плоскостях {110}, {112} или {123} по направлениям <111>. Напомним, что условием активации k-й системы скольжения является достижение
по направлениям 110 (иначе говоря, в системе скольжения {111}, <110>). В ОЦК – решетке трансляционное движение краевых дислокаций осуществляется в плоскостях {110}, {112} или {123} по направлениям <111>. Напомним, что условием активации k-й системы скольжения является достижение
243

касательного напряжения в ней некоторого критического напряж е- ния τck :
|
σ : n(k )b(k ) = τ(ck ) , |
, (8.1) |
|
|
k |
где n k b k |
( ) – ориентационный тензор k-ой системы скольже- |
|
|
k |
|
ния. Чаще в литературе в качестве ориентационного тензора M(k ) k-ой системы используется симметричная часть диадного произв е- дения
M k |
1 |
n k b k |
b k n k |
, . |
|
||||
2 |
|
|
k |
|
|
|
|
|
|
Нетрудно видеть, что ориентационный тензор M( k ) является девиатором.
Условие (8.1), как отмечено выше, обычно называется законом Шмида, устанавливающим момент начала неупругого дефо р- мирования при достижении в системе скольжения критического значения касательного напряжения . При реализации (8.1) в одной системе скольжения говорят об одиночном скольжении; если кр и- сталл подвергается нагружению, при котором дислокации начин а- ют скользить в двух и ли более системах, то говорят о двойном или множественном скольжении. В соответствии с уравнением Оров а- на при наличии К активных систем скольжения (СС) (т.е. СС, для которых удовлетворяется закон Шмида (8.1)) в произвольный момент деформирования девиатор пластической составляющей те н- зора деформации скорости определяется соотношением:
K
dp = M(k ) γ(k ) , (8.2)
k =1
где γ(k ) – скорость сдвига в k-ой СС.
Соотношение (8.1) в физической теории пластичности часто используется в качестве критерия текучести не только для опред е- ления момента начала текучести, но и для произвольного момента
деформирования. В этом случае τ(ck ) зависит от истории деформи-
рования. При одиночном скольжении по k-й активной системе скольжения происходит обычно увеличение критического напр я-
жения τ(ck ) активной системы, называемое деформационным («ак-
тивным») упрочнением и зависящее от величины сдвига. А что будет происходить в других СС, даже если они не являются в да н- ный момент активными? Из физических соображений нетрудно предположить, что изменение плотности дислокаций в активных СС, сопровождающее пластическую деформ ацию, неминуемо повлияет на поведение дислокаций в других СС. Действительно, н а-
244

ряду с активным упрочнением в экспериментах наблюдается ув е- личение критических напряжений в других системах, где сдвиг в процессе одиночного скольжения отсутствует . Такое увеличение
τ(cl ) , l k называется скрытым («латентным») упрочнением . По-
следнее обусловлено увеличением плотности дислокаций в акти в- ных системах скольжения, являющихся препятствиями (дислок а- циями леса) для ди слокаций других систем скольжения, равно как и возникновением других барьеров дислокационного происхожд е- ния.
Как показывают эксперименты, при множественном скольж е- нии увеличение критического напряжения сдвига на единицу сдв и- га оказывается большим, чем при одиночном скольжении. Каким образом это можно ввести в физическую модель? Тейлором был предложен закон изотропного упрочнения, согласно которому приращения критических касательных напряжений во всех актив-
ных системах скольжения одинаковы и определяются сум мар-
ным сдвигом по всем активным системам . Указанный закон широко используется в различных модификациях физической теории пластичности. Кроме того, во многих работах принимается, что деформационное и скрытое упро чнения одинаковы; в настоящей работе данное предположение также будет использоваться. В то же время следует отметить, что экспериментальные исследования свидетельствуют о некотором превышении латентного упрочнения над деформационным.
При построении определяющих соотношений для монокр и- сталла часто используется формализм теории пластического теч е- ния. В последней одним из главных понятий является понятие п о- верхности текучести. Одним из распространенных вариантов ура в- нения, определяющего поверхность текучести монокристалла, является соотношение (8.1), которое можно записать в виде
f (S) = M(k ) : S - ( τ(ck ) ) = 0, k = 1, K , (8.3)
где K – полное число СС рассматриваемого монокристалла. Отметим, что в последнем соотношении полагается равенство
пределов текучести в k-й системе скольжения при «прямом» и «реверсивном» нагружении, и тогда модель не будет описывать хор о- шо известный эффект Баушингера (см. гл.2). Как этого избежать? Указанное ограничение может быть легко устранено путем пер е- определения понятия системы скольжения, когда система скол ь- жения определяется нормалью к плоскости скольжения и «пол о- жительным» и «отрицательным» направлениями скольжения в ней краевых дислокаций, т.е. осуществляется удвоение числа систем скольжения:
245

|
M(k ) : S |
|
τ(k ) |
|
|
|
f (S) = |
- |
= 0, k = 1,2K . (8.4) |
||||
|
|
|
c |
|
|
|
Далее под К будет пониматься именно число систем скол ь- жения, равное удвоенному числу кристаллографических систем скольжения.
Полагая неизменным положение кристаллографических осей (при рассмотрении больших деформаций и разворотов монокр и- сталлов – в локальной системе координат, связанной с монокр и- сталлом), нетрудно видеть, что соотношения (8.3) (или (8.4)) представляют собой совокупность К линейных уравнений относительно компонент девиатора напряжений S. Следовательно, в пространстве напряжений соотношения (8.3) (или (8.4)) определяют К гиперплоскостей, или К-гранник, называемый многогранником текучести. Например, для ГЦК -кристаллов поверхность текучести представляет собой 24 -гранник.
Нетрудно видеть, что градиент поверхности текучести в пр о- странстве напряжений определяется соотношением
f (S) |
|
|
|
|
|
= M(k ) , k = 1, K . |
(8.5) |
||||
S |
|||||
|
|
|
|
||
Если изображающая точка в пространстве напряжений (ИТН) находится на одной из граней м ногогранника текучести (т.е. выполняются условия пластического деформирования), для опред е- ленности – на грани с номером l, то активной является система скольжения l и из сопоставления (8.2) и (8.5) нетрудно видеть, что направление приращения пластической деформации определяется градиентом к поверхности текучести. И наче говоря, в данном случае выполняется принцип градиентальности для поверхности тек у- чести, т.е. справедлив ассоциированный закон пластического т е- чения. При расположении ИТН на ребре многогранника текучести приращение девиатора пластической деформации dep имеет направление, определяемое линейной комбинацией нормалей к пер е- секающимся граням. Аналогичным образом определяется напра в- ление dep при нахождении ИТН в вершине многогранника (напра в- ление dep лежит внутри конуса, ограниченного нормалями к пер е- секающимся граням).
Наличие сингулярной поверхности текучести порождает о п- ределенные трудности при построении соотношений теории пл а- стичности (аналогичная ситуация возникает, например, при и с- пользовании критерия Треска -Сен-Венана в теории пластического течения). В связи с этим целесообразными следует признать п о- пытки замены условий текучести с сингулярностями (вида (8.3)– (8.4)) регулярными (гладкими) условиями. Одна из таких попыток предпринята в работе [37]. Условия текучести в цитируемой раб о- те представлено в виде
246
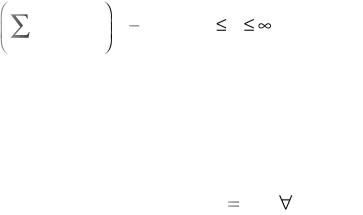
|
|
|
|
|
1/q |
|
|
|
f (S) = |
|
M(k ) : S |
|
q |
τ |
c |
= 0, 2 q . |
(8.6) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||
Можно показать, что соотношение (8.6) |
определяет гладкую, |
|||||||
ограниченную и строго выпуклую поверхность в пространстве н а- пряжений. Отметим, что условие (8.6) может быть легко модифицировано для случая различных критических напряжений на плоскостях скольжения. Кроме того, можно показать, что при q 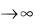 поверхность, описываемая соотношением (8.6), стремится к по-
поверхность, описываемая соотношением (8.6), стремится к по-
верхности многогранника (8.3) (при τck τc k ), оставаясь внут-
ри многогранника. В отличие от многогранника поверхность (8.6) не имеет особенностей, что позволяет достаточно просто записать соотношения ассоциированного закона пластического течения.
Определение функции текучести и принцип градиентальности в сочетании с тем или иным законом упрочнения, определяющим изменения критических напряжений в системах скольжения в пр о- цессе деформирования, образуют базис, достаточный для описания поведения монокристаллов.
247
О теориях пластичности для поликристаллов
Определенные успехи, достигнутые при построении моделей монокристалла, побудили исследователей к использованию п о- следних для описания поведения поликристаллов. Как и ранее, о г- раничимся случаем малых деформаций.
Основной особенностью поликристаллов в сравнении с мон о- кристаллами является наличие в первых множества различно ор и- ентированных кристаллических микрообъектов (с относительно правильным строением кристаллической решетки) и существов а- ние границ между этими микрообъектами . В дальнейшем указанные области для краткости будем называть зернами.
Границы зерен оказывают на повед ение поликристаллов весьма существенное влияние . Границы представляют собой спе-
цифические области дефектной структуры с характерной тол-
щиной 0,1–0,6 мкм (при размерах зерен 20 –50 мкм) и плотностью дислокаций в несколько раз выше, чем в зернах, что обусловливает и повышенную удельную внутреннюю энергию границ по сра в- нению с зернами. В связи с этим границы зерен могут выступать и как специфический механизм неупругого деформирования (так н а- зываемого зернограничного скольжения) . Возможно, более существенное влияние на процесс неупругого деформирования они ок а- зывают как генераторы дислокаций и как «устройства», реал и- зующие аккомодационные механизмы.
Кроме того, на границах зерен реализуются ограничения, накладываемые на пластическое деформи рование зерна раз-
лично ориентированными соседними зернами; например, скольж е- ние дислокаций в одном зерне не может свободно продолжаться в соседнем с ним зерне в силу несовпадения кристаллографических систем. Наличие этих разориентировок СС соседних зерен с лужит одним из основных источников активизации ротационных мод д е- формирования поликристаллов, является причиной существенной неоднородности деформирования зерен и возникновения конце н- траторов напряжений (особенно – в так называемых тройных стыках зерен). В большинстве работ по ФТП учитывается именно вт о- рой аспект влияния границ, связанный со стеснением пластич е- ских деформаций за счет разориентировки соседних зерен.
248
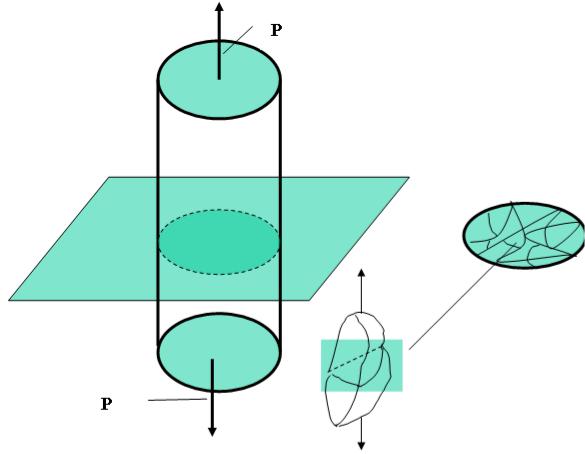
Модель Закса
Одной из первых попыток построения одномерной модели поликристалла на осно ве рассмотрения совокупности монокр и- сталлов была модель Закса [71] . В данной модели зерна полагались ориентированными хаотически (по равномерному закону), взаимодействием между зернами пренебрегалось (в силу чего эту модель можно назвать «полностью несовместной»).
Рис. 8.1. Схема к модели Закса
Модель Закса в исходной формулировке предназначена тол ь- ко для определения предела текучести при одноосном растяжении поликристаллического образца по известному значению критич е- ского напряжения сдвига в СС монокристаллов -зерен и заданному закону распределения ориентаций кристаллографических систем координат (КСК) зерен по отношению к лабораторной системе к о- ординат (ЛСК).
Рассмотрим одноосное нагружение цилиндрического образца из поликристаллического материала; ось х1 с единичным вектором базиса е1 направим вдоль оси образца. В рассматриваемом случае все компоненты тензора напряжений Коши σ за исключением σ11
полагаются нулевыми. Мысленно пересечем образец плоскостью, перпендикулярной его оси, и выделим все зерна, пересекаемые данным сечением (рис.8.1). В модели Закса полагается, что каждое
249

из зерен также находится в состоянии однородного одноосного растяжения (сжатия), как и образец в целом, однако величины н а- пряжений σ11 в каждом зерне могут отличаться от напряжений в
других зернах. Величина напряжений в каждом зерне определяется из условия достижения касательным напряжением хотя бы в одной СС («слабейшем звене ») величины критического напряжения сдв и- га τc , считающейся известной для анализируемого типа криста л-
литов-зерен и одинаковой для всех зерен. Таким образом, для ка ж- дого из зерен, попавших на введенное сечение, зная ориентацию КСК относительно ЛСК, вначале оп ределяется максимальный фак-
тор Шмида M(k ) = |
|
σ |
|
: b(k )n(k ) , ( |
) (для рассматриваемого случая |
|||||
|
|
|
||||||||
S |
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k ) |
|
|
|
|
|
одноосного нагружения M(k ) = e e : b(k )n(k ) , ( |
) ). Тогда для каждо- |
|||||||||
|
|
|
|
|
S |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
(k ) |
|
|
|
го п-го зерна напряжение |
σ(n) |
определяется как σ(n) |
τ |
/ max M(k ) . |
||||||
|
|
|
|
|
11 |
|
11 |
c |
k |
S |
|
|
|
|
|
|
|
|
|
|
|
Обозначив через S( n ) площадь поперечного сечения n –го зерна, пересекаемого введенным сечением, а через S – площадь поперечного сечения образца в целом, предел текучести при одноосном нагружении определяется тогда соотношением
N
σ11(n) S(n)
σ |
|
= |
n=1 |
|
. |
s |
|
|
|||
|
|
|
S |
||
|
|
|
|
||
Расчеты по модели Закса дают значение макроскопического напряжения текучести σs , равное 2,2 c . Хотя полученный резуль-
тат существенно (примерно на 30%) отличается от экспериме н- тально определенного предела текучести, его все же следует пр и- знать удовлетворительным для своего времени.
К основным недостаткам модели Закса относятся невыполн е- ние условий равновесия и совместности деформаций соседних з е- рен, неучет упругих деформаций. Модель Закса может быть и с- пользована для определения предела текучести при одноосно м нагружении, для построения кривой – требуются дополнительные предположения.
требуются дополнительные предположения.
Модель Тейлора
Вероятно, первой достаточно реалистичной попыткой уст а- новления связи – при одноосном нагружении поликристалла на основе соотношений для монокристалла можно п ризнать модель Тейлора [84]. При её построении Тейлором использованы следу ю- щие гипотезы:
при одноосном нагружении поликристалла на основе соотношений для монокристалла можно п ризнать модель Тейлора [84]. При её построении Тейлором использованы следу ю- щие гипотезы:
250
