
Сопротивление материалов конспект лекций
..pdf
М1 М2 М3 М4
М2 М3 М4
а |
1000 |
|
|
|
|
500 |
|
|
|
|
|
200 |
200 |
|
|
Мк, Н·м |
|
||
|
|
|
||
|
|
|
|
|
|
М2 |
М1 |
М3 |
М4 |
б |
|
500 |
|
200 |
|
Мк, Н·м |
200 |
||
|
|
|
|
|
|
500 |
|
|
|
Рис. 6.5
Из условия прочности полярный момент сопротивления для варианта рис. 6.5, а – в 2 раза больше, чем для варианта б.
Отношение диаметров |
dа |
= 2 ≈1, 26. |
|
dб |
|
При постоянном сечении вала по всей его длине отношение весов равно отношению площадей подобранных сечений:
γАаl = dа2 ≈1,6 раза.
γАбl dб2
Следовательно, при той же прочности вала для варианта рис. 6.5, б расход материала будет в 1,6 раза меньше.
61

Лекция 7. ИЗГИБ
7.1. Общие понятия
Изгибом называется вид нагружения, при котором в поперечном сечении стержня возникает изгибающий момент. Если в сечении возникает только изгибающий момент, то изгиб называется чистым.
Плоский изгиб – случай, когда изогнутая ось представлена плоской кривой. Если плоский изгиб лежит в плоскости действия сил, то изгиб называется прямым.
Стержень, работающий на изгиб, называется балкой. Стержневая система, элементы которой работают на изгиб, на-
зывается рамой.
Если в сечении кроме изгибающего момента возникает поперечная сила, то изгиб называется поперечным.
Статически определимые системы – системы, реакции опор в которых могут быть определены из условий равновесия статики.
Статически неопределимые системы – системы, в которых число неизвестных больше числа независимых уравнений равновесия статики.
Виды опор
Заделка (рис. 7.1):
Рис. 7.1
Шарнирно-неподвижная опора (рис. 7.2):
или
Рис. 7.2
62

Шарнирно-подвижная опора (рис. 7.3):
Рис. 7.3
Определение внутренних силовых факторов при изгибе
Используем метод сечений (рис. 7.4)
Рис. 7.4
Внутренние силовые факторы определяются из условия равновесия выделенной части балки.
ΣFy = 0: F1 −q(z −c) −Qy = 0, Qy = F1 −q(z −c).
63

ΣM (0) = 0: − F1z −M +q(z −c) z −2 c + M x = 0, M x = F1z + M −q (z −2c)2 .
Обобщая полученные результаты, можно выделить следующие правила:
• Поперечная сила Qy равна сумме проекций всех сил, прило-
женных по одну сторону от сечения на плоскость сечения.
• Изгибающий момент M x равен сумме моментов всех сил, при-
ложенных по одну сторону от сечения относительно центра тяжести системы.
•Поперечная сила в сечении считается положительной, если равнодействующая внешних сил, приложенных слева от сечения, направлена вверх, а справа от сечения – вниз. Если же равнодействующая внешних сил слева от сечения направлена вниз, а справа – вверх, поперечная сила отрицательна (рис. 7.5).
•Правило знаков:
а) для поперечной силы Qy:
Рис. 7.5
б) для изгибающего момента M x (рис. 7.6):
Рис. 7.6
64
•Изгибающий момент считается положительным, если он вызывает сжатие верхних волокон балки и растяжение нижних.
•При растяжении верхних волокон изгибающий момент отрицательный (см. рис. 7.6).
Дифференциальные зависимости между поперечной силой Qy ,
изгибающим моментом M x |
и интенсивностью распределенной на- |
||||||
грузки q: |
|
|
|
|
|
|
|
|
dQy |
= q, |
dM |
x = Q |
, |
d 2M |
x = q. |
|
dz |
dz |
dz2 |
||||
|
|
y |
|
|
|||
Эти дифференциальные зависимости оказывают неоценимую помощь при построении эпюр внутренних силовых факторов и их проверке.
7.2. Правила проверки (построения) эпюр M x и Qy
Если балка нагружена равномерно распределенной нагрузкой, то, очевидно, Qy будет линейной, а M x – квадратичной функцией
координаты z. Если балка нагружена сосредоточенными силами и моментами (q = 0), то поперечная сила будет постоянной, а момент – линейной функцией координаты z. В точках приложения сосредоточенных сил эпюра Qy претерпевает скачок на величину
внешней силы, а на эпюре M x возникает излом, поскольку производные момента слева и справа от этих точек имеют различные значения. В точках приложения сосредоточенных моментов эпюра M x претерпевает скачок на величину внешнего момента. В сечениях, в которых поперечная сила Qy равна нулю, в зависимости от знака q
на эпюре M x наблюдается максимум или минимум (q > 0, если распределенная нагрузка направлена вверх).
65
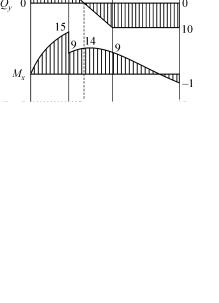
|
|
|
Пример |
|
|
|
|
Дано: |
|
|
|
|
b =3 м, |
|
|
|
|
M = 6 кН м, |
|
|
|
|
q =10 |
кН, |
|
|
|
|
м |
|
|
|
F = 20 кН, |
|
|
|
|
l = 4 м, |
|
|
|
|
a =1 м (рис. 7.7). |
|
|
|
|
Решение: |
|
|
|
|
|
ΣFy = 0, |
|
|
|
F −q 3 + RA = 0, |
|
|
|
|
RA |
= −F +q 3 = |
|
|
|
= −20 |
+10 3 =10 кН, |
|
|
|
ΣM A = Fl +qb(l −b / 2) + |
|
Рис. 7.7 |
|
|
+ M −M A = 0, |
|
M A = −Fl +qb l − b |
|
+ M = −20 4 +10 3 2,5 +6 = |
||
|
2 |
|
|
|
= −80 +75 +6 =1 кН·м,
0 ≤ z1 ≤ a:
Qy = F −qz1 = 20 −10z1,
Qy(0) = 20 кН, Qy(1м) =10 кН,
|
|
= Fz −q |
z2 |
= 20z −5z2 |
|
|
M |
x |
1 |
, |
|||
|
||||||
|
1 |
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
M x(0) = 0, M x(1м) =15 кН·м, 0 ≤ z2 ≤ 2 м:
Qy = F −q(1+ z2 ) = 20 −10(1+ z2 ),
66
Qy(0) =10 кН, Qy(2м) = −10 кН,
M x = F (1+ z2 ) −q |
(z2 +1)2 |
−M = 20(1+ z2 ) −5(z2 +1)2 −6, |
|
|
|
2 |
|
M x(0) =9 к·Нм, |
M x(2м) =9 кН·м, |
||
M xэк = 20 2 −10 |
22 |
−6 =14 |
кН·м. |
|
2 |
|
|
0 ≤ z3 ≤1 м:
Qy = −RA = −10 кН,
M x = −M A + RA z3 = −1+10z3 ,
M x(0) = −1 кН·м, M x(1м) =9 кН·м.
7.3. Условие прочности при чистом изгибе. Рациональная форма поперечного сечения при изгибе
Нормальные напряжения при чистом изгибе распределяются в поперечном сечении по линейному закону, пропорционально расстоянию от нейтральной оси (рис. 7.8):
Рис. 7.8
67
σ = |
M x Y. |
(7.1) |
|
Jx |
|
Максимальные по величине напряжения возникают в наиболее удаленных от нейтральной оси точках сечения:
σmax = M x Ymax .
Jx
Для пластичных материалов рациональным является сечение, симметричное относительно нейтральной оси. Условие прочности имеет вид
|
σ |
|
max |
= |
M x |
≤[σ], |
|
|
|
(7.2) |
||||
|
|
|
|
|
||||||||||
|
|
Wx |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Wx – осевой момент сопротивления, Wx |
= |
Jx |
. |
|||||||||||
|
|
|||||||||||||
Y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
max |
||
|
|
|
|
(σпчс >> σпчp ) |
|
|
|
|||||||
Для хрупких материалов |
|
рациональное сечение – |
||||||||||||
несимметричное относительно нейтральной оси. |
||||||||||||||
Условие прочности: |
|
|
|
|
|
|
|
|
|
|
|
|
||
σp |
= |
M x |
|
Y p |
|
≤[σ] |
|
, |
|
|
|
|||
|
|
p |
|
|
|
|||||||||
max |
|
|
|
|
max |
|
|
|
|
|
||||
|
|
|
|
Jx |
|
|
|
|
|
|
|
|||
σс |
= |
M x |
Y с |
|
≤[σ] |
|
, |
|
(7.3) |
|||||
|
|
с |
|
|||||||||||
max |
|
|
|
|
max |
|
|
|
|
|
||||
|
|
|
|
Jx |
|
|
|
|
|
|
|
|||
где Ymaxp и Ymaxс – расстояние от нейтральной оси до наиболее удаленных точек сечения соответственно в растянутой и сжатой зонах;
[σ]p и [σ]с – допускаемые напряжения на растяжение и сжатие.
Наиболее экономичными являются такие формы поперечных сечений, для которых с наименьшим расходом материала обеспечивается наибольшая величина момента сопротивления Wx . Для этого
достижения необходимо распределять основную часть площади сечения как можно дальше от нейтральной оси. Для пластичных материалов это двутавр, швеллер, кольцевое сечение, для хрупких материалов – сечения в виде тавра, П-образного сечения.
68
7.4. Напряжения при поперечном изгибе
При поперечном изгибе в поперечных сечениях вместе с нормальными напряжениями действуют и касательные напряжения τ. При этом из-за наличия поперечной силы гипотеза плоских сечений не выполняется.
Однако нарушение гипотезы плоских сечений оказывает незначительное влияние на распределение нормальных напряжений, поэтому при поперечном изгибе для вычисления нормальных напряжений применима формула чистого изгиба.
Из-за наличия поперечной силы в сечении возникает и касательное напряжение. Касательные напряжения определяются по формуле Журавского:
|
Q |
y |
Sотс |
|
|
|
τ = |
|
x |
, |
(7.4) |
||
Jxb( y) |
||||||
|
|
|
||||
где Qy – поперечная сила; Sxотс – статический момент части площади
сечения, расположенной по одну сторону от рассматриваемого слоя относительно главной оси х; Jx – момент инерции всего сечения; b( y) – ширина рассматриваемого слоя.
7.5.Распределение касательных напряжений
впоперечном сечении
1.Массивные профили:
а) прямоугольное сечение (рис. 7.9):
Рис. 7.9
69
б) круглое сечение (рис. 7.10)
Рис. 7.10
В массивных профилях касательные напряжения существенно меньше нормальных. Так, для консольной балки прямоугольного по-
перечного сечения |
|
|
τmax |
|
|
= |
h |
, поэтому при прочностных расчетах |
|
|
|
|
|||||||
|
σmax |
|
4l |
||||||
|
|
||||||||
|
|
|
|
|
|||||
касательными напряжениями пренебрегают.
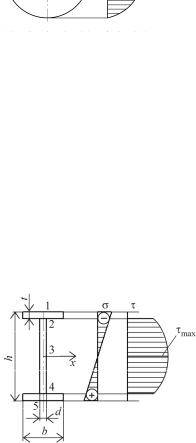
2. Тонкостенный профиль – двутавр (рис. 7.11):
Рис. 7.11
Для тонкостенных профилей (например, двутавра) при нагрузках, вызывающих большую поперечную силу, производится проверка прочности по максимальным касательным напряжениям в точке 3 на нейтральной оси (рис. 7.11):
|
τ |
|
max |
= |
|
|
Qy |
|
max Sx* |
≤[τ], |
(7.5) |
|
|
||||||||||
|
|
|
|
||||||||
|
|
|
|
Jxd |
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
70
