
Сопротивление материалов конспект лекций
..pdf
Условие прочности имеет вид
σII |
= σ – µ(σ |
2 |
+ σ |
3 |
) ≤[σ]. |
(4.24) |
экв |
1 |
|
|
|
Эта теория прочности так же, как и первая, применима к материалам в хрупком состоянии (высокопрочные инструментальные стали, чугун).
Третья теория прочности: теория наибольших касательных напряжений
Согласно этой теории напряженные состояния будут равноопасными, если их максимальные касательные напряжения равны.
Ввиду того, что при сложном напряженном состоянии элемен-
таτmax = |
σ1 – σ3 |
, а при одноосном растяжении образца |
τmax = |
σэкв |
, ус- |
||||
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
ловие прочности приобретает вид |
|
|
|
|
|
||||
|
|
σIII |
= σ – σ |
3 |
≤[σ]. |
|
(4.25) |
||
|
|
экв |
1 |
|
|
|
|
||
Третья теория дает хорошие результаты для пластичных материалов с одинаковым пределом текучести при растяжении и сжатии.
Четвертая теория прочности: теория удельной потенциальной энергии изменения формы
Согласно этой теории напряженные состояния равноопасны, если для них равны удельные потенциальные энергии изменения формы.
При сложном напряженном состоянии удельная потенциальная энергия изменения формы определяется по выражению
uф =16+Eµ (σ1 – σ2 )2 +(σ2 – σ3 )2 +(σ3 – σ1 )2 .
При одноосном растяжении образца, когда σ1 = σэкв, а σ2 = σ3 = 0,
uф =16+Eµ 2σэкв2 .
41

Следовательно, условие прочности имеет вид
σIV |
= |
1 |
(σ – σ |
|
)2 +(σ |
|
– σ |
|
)2 +(σ |
|
– σ )2 |
|
≤[σ]. |
(4.26) |
|
экв |
|
2 |
|
1 |
2 |
|
2 |
|
3 |
|
3 |
1 |
|
|
|
Теория дает хорошие результаты для пластичных материалов, одинаково работающих на растяжение и сжатие. Преимуществом четвертой теории перед третьей является то, что в ней учитывается влияние всех трех главных напряжений.
Теория прочности Мора
Условие прочности имеет вид
σV |
= σ – kσ |
3 |
≤[σ]. |
(4.27) |
экв |
1 |
|
|
Здесь коэффициент неравнопрочности
= σр
k σпчс , пч
где σпчр – предел прочности при растяжении; σспч – предел прочности
при сжатии.
Применяется данная теория прочности для материалов, поразному сопротивляющихся растяжению и сжатию.
4.6. Чистый сдвиг
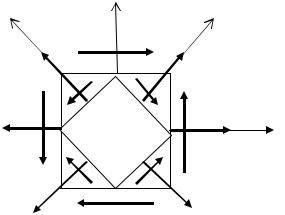
Чистым сдвигом называется такой случай плоского напряженного состояния, когда по двум взаимно перпендикулярным площадкам действуют только касательные напряжения (рис. 4.10).
Главные площадки наклонены к граням элемента под углом 45°. По главным площадкам действуют главные напряжения σ1 = τ
и σ3 = –τ; σ2 = 0.
42

|
τ |
σ1 |
|
|
∆S |
|||
|
|
|
α = 45° |
|
|
|||
|
σ3 |
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
γ |
|||
|
|
|
|
|
|
|||
|
|
σ3 |
а τ |
|
||||
|
|
|
|
|
|
|
||
σ1 |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 4.10 |
|
|
|
|
Рис. 4.11 |
||
Взаимное перемещение двух параллельных площадок, отстоящих друг от друга на расстоянии а (рис. 4.11), называется абсолют-
ным сдвигом ∆S, а отношение γ = ∆aS – относительным сдвигом или
угловой деформацией. Экспериментально установлено, что между τ и γ существует линейная зависимость
τ =Gγ, |
(4.28) |
которая отражает закон Гука при сдвиге, где G – модуль сдвига. Между тремя константами материала Е, G и µ существует зави-
симость
G = 2(1E+µ).
По разным теориям прочности получим различные соотношения между допускаемыми нормальными и касательными напряжениями.
По третьей теории прочности [τ]= 0,5[σ], по теории энергии
формоизменения [τ]= 0,58[σ], по теории прочности Мора
[τ]= 1[+σ]k .
43
Пример 1
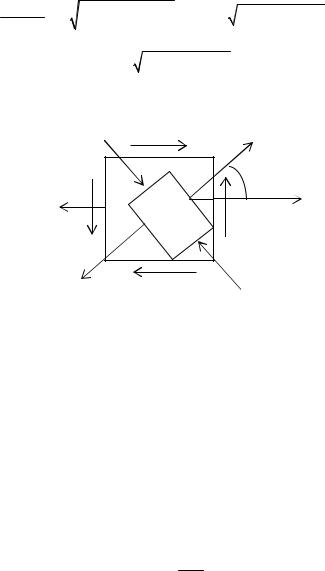
В опасной точке детали выделен элемент, находящийся в условиях плоского напряженного состояния (рис. 4.12).
y1 |
y |
x1 |
|
||
|
|
|
|
|
40 |
σy1 = 10 МПа |
|
σх1 = 110 МПа |
40
α
120
x
Рис. 4.12
σх= 120 МПа,
σy = 0,
τх= –40 МПа, α = 40°.
Материал сталь 40 (σт =340 МПа). Определить:
1)главные напряжения и положение главных площадок;
2)напряжения в элементе, повернутом к исходному на 40°;
3)коэффициент запаса прочности, используя четвертую теорию прочности.
Решение:
1. Определим положение главных площадок по формуле (4.8):
tg2α0 = − |
2τx |
|
= − |
2(−40) |
= 0,67, |
||
|
|
120 −0 |
|||||
|
σx −σy |
|
|||||
α0 =16°54', |
α0 + |
π |
=106°54'. |
||||
2 |
|||||||
|
|
|
|
|
|
||
44
|
|
Находим величину главных напряжений по формуле (4.9): |
|||||
σ1 |
= |
σx +σy + |
1 |
(σx −σy )2 |
+4τ2x = 60 + 1 |
1202 +4(−40)2 |
=132 МПа, |
|
|
2 |
2 |
|
2 |
|
|
|
|
|
σ3 |
= 60 − 1 |
1202 +4(−40)2 |
= −12 МПа. |
|
|
|
|
|
2 |
|
|
|
|
|
Полученные результаты представлены на рис. 4.13. |
|
||||
|
|
σ3 = 12 МПа |
40 |
σ1 = 132 |
|
||
|
|
|
|
|
|
α0 = 16°54' |
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
Рис. 4.13 |
|
|
|
2. Напряжения на гранях элемента, повернутого на угол 40°, |
||||||
найдем по формулам (4.3), (4.5), (4.6): |
|
|
|||||
σх1 =1202 +1202 cos80°−(−40)sin80° =110 МПа,
σy1 =1202 −1202 cos80°+(−40)sin80° =10 МПа,
τх1 =1202 sin80°+(−40)cos80°=52 МПа.
Результаты расчетов представлены на рис. 4.12. 3. Коэффициент запаса прочности
n = σσIVт ,
экв
45
где по (4.26)
|
|
σIV |
|
= |
1 σ2 |
+σ2 |
+(σ |
|
−σ )2 |
|
= |
|
|
|
экв |
|
2 1 |
3 |
|
3 |
|
1 |
|
|
|
= |
1 |
1322 |
+( |
−12)2 +(−12 −132)2 |
=138,4 МПа, |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n =138,4340 = 2,46 >[n] =1,5.
Прочность детали обеспечена.
Пример 2
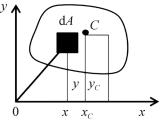
На гранях элемента, находящегося в объемном напряженном состоянии, заданы напряжения:
σ1 = 60 МПа,
40 МПа σ2 = 40 МПа,
σ3 = −90 МПа (рис. 4.14).
60 МПа |
|
Материал |
детали – чугун |
марки |
|||
|
|
||||||
СЧ 15-32 с характеристиками прочности |
|||||||
σпчр |
=147 МПа, |
σпчс = 638 МПа. |
|
||||
90 МПа |
|
Решение: |
|
|
|||
Рис. 4.14 |
|
|
|
||||
|
Оценим прочность детали, воспользо- |
||||||
вавшись теорией прочности Мора: |
|
||||||
σV |
= σ −kσ |
3 |
≤[σ], |
(4.29) |
|||
экв |
1 |
|
|
|
|
||
где k – коэффициент неравнопрочности: |
|
|
|||||
k = |
σр |
147 |
|
= 0,23, |
|
||
|
пч = |
|
|
|
|||
|
σпчс |
638 |
|
|
|
||
σэквV = 60 −0,23(−90) =81 МПа. |
|
||||||
n =147 |
=1,81 < [n] = 2,5. |
|
|||||
81 |
|
|
|
|
|
|
|
Прочность детали не обеспечена.
46
Лекция 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.1. Общие определения
Прочность бруса не всегда зависит только от площади поперечного сечения, как это имеет место при растяжении и сжатии. Как бы вы ни поворачивали стержень относительно продольной оси, условие прочности будет всегда иметь вид
σ = |
N |
≤ [σ]. |
(5.1) |
|
А |
||||
|
|
|
Другую картину мы имеем при изгибе. Так, при изгибе относительно одной из осей в поперечном сечении мы имеем при одном и том же действующем изгибающем моменте один эффект с точки зрения прогибов и прочности, а относительно другой, перпендикулярной оси – отличающийся от первого. Следовательно, при изгибе условие прочности зависит не только от площади поперечного сечения, но и от какого-то другого геометрического параметра (формы).
Для плоской фигуры (рис. 5.1) наиболее часто рассматриваются следующие геометрические характеристики, кроме известных (площадь А, длина l): статические моменты:
Sx = ∫ ydА, Sy = ∫ xdА.
F F
Статические моменты могут быть положительными, отрицательными и равными нулю. Они измеряются в единицах длины в кубе – м3, см3, мм3.
Оси, относительно которых стати- Рис. 5.1 ческие моменты равны нулю, называются центральными. Они всегда
проходят через центр тяжести фигуры. На основании теоремы о моменте равнодействующей
47
Sx = АyС, Sy = АxС. |
(5.2) |
Из этих соотношений может быть определен центр тяжести для простой фигуры.
x |
= |
Sy |
, y = |
S |
х |
. |
(5.3) |
А |
|
|
|||||
С |
|
С |
А |
|
|||
Координаты центра тяжести сложных фигур:
|
n |
|
|
n |
|
|
|
|
n |
|
n |
|
|
||
x = |
∑Syi |
= |
|
∑ Аi yi |
|
|
= |
|
∑Sxi |
= |
∑ Аi xi |
|
|
||
i=1 |
|
i=1 |
, |
y |
|
i=1 |
|
i=1 |
. |
(5.4) |
|||||
n |
n |
n |
n |
||||||||||||
С |
|
|
|
С |
|
|
|
|
|
||||||
|
∑ Аi |
|
|
∑ Аi |
|
|
|
|
∑ Аi |
|
∑ Аi |
|
|
||
|
i=1 |
|
|
i=1 |
|
|
|
|
i=1 |
|
i=1 |
|
|
||
Осевые моменты инерции: |
|
|
|
|
|
|
|
|
|
|
|||||
|
Jx |
= ∫ y2dА, |
J y |
= ∫ x2dА. |
|
|
|
(5.5) |
|||||||
|
|
|
|
F |
|
|
|
F |
|
|
|
|
|||
Полярный момент инерции
Jρ = ∫ρ2dА= Jx + J y . |
(5.6) |
А |
|
Центробежный момент инерции |
|
Jxy = ∫ x ydА. |
(5.7) |
А |
|
Осевые и полярный моменты инерции всегда больше нуля. Центробежный момент инерции может быть отрицательным, положительным и равным нулю. Моменты инерции относительно центральных осей называются центральными моментами инерции.
Оси, относительно которых центробежный момент инерции равен нулю, называют главными. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
48
5.2. Изменение моментов инерции при параллельном переносе осей
Если оси х, у параллельны центральным осям хС, уС (рис. 5.2), то справедливы следующие соотношения:
Jx |
= Jx +b2 А, |
|
|
yС |
|
|
|
|
|
|
|
||
1 |
С |
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
= J y |
+a2 А |
|
|
|
|
|
dA |
|
|
|||
1 |
С |
|
|
|
|
|
|
|
|
|
|||
Jx y |
= Jx y |
|
+abА, |
(5.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y |
|
|
||||
1 1 |
С С |
|
|
|
С |
|
|
|
|
|
|
||
где a и b – координаты точки 0 (с уче- |
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
b |
хC |
||||||||
|
а |
||||||||||||
том знаков), т.е. нового начала коорди- |
01 |
|
|
|
|
|
|
|
х1 |
||||
нат в старой системе координат хC, уC. |
|
|
|
|
|
|
|
||||||
Первые слагаемые в правых частях |
|
|
Рис. 5.2 |
|
|
||||||||
равенств (5.7) являются собственными моментами инерции фигуры, а вторые слагаемые – переносными мо-
ментами инерции. Моменты инерции относительно осей, параллельных центральным, всегда увеличиваются по отношению к центральным на величину, равную произведению площади сечения на квадрат расстояния между рассматриваемыми осями.
Для сложных сечений моменты инерции связаны следующими соотношениями:
n |
n |
Jx = ∑Jxi , J y = ∑J yi , |
|
i=1 |
i=1 |
n |
|
Jxy = ∑Jxi yi . |
(5.9) |
i=1
5.3. Изменение моментов инерции при повороте осей координат
При повороте осей (х1; у1) на какой-либо угол α по отношению к исходным (рис. 5.3, а) моменты инерции изменяются:
Jx |
= Jx cos2 α+ J y sin2 α− Jxy sin 2α, |
(5.10а) |
1 |
|
|
J y |
= Jx sin2 α+ J y cos2 α+ Jxy sin 2α, |
(5.10б) |
1 |
|
|
49

|
|
|
|
|
|
Jx y |
= |
Jx − J y |
sin 2α+ Jxy cos 2α. |
(5.11) |
|||||||||
|
|
2 |
|||||||||||||||||
|
|
1 1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
у1 |
у |
|
|
|
|
у |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
||||
|
|
|
|
|
∆А |
|
|
у1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
α0 |
|
|||
|
|
|
|
|
|
|
х1 |
|
х |
|
|
|
|
|
х |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
б |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рис. 5.3
Эти зависимости справедливы только для осей с общим началом координат. Положительный угол α отсчитывается от оси х в направлении кратчайшего поворота ее до совмещения с осью у.
5.4.Определение положения главных осей
иглавных моментов инерции
Положение главных осей находится по формуле
tg2α0 = − |
2Jxy |
, |
(5.12) |
|
|||
|
Jx − J y |
|
|
где α0 – угол, на который нужно повернуть оси х и у, чтобы получить положение главных осей. При α0 > 0 поворот оси х до совмещения с главной осью производится против часовой стрелки (рис. 5.3, б).
Главные моменты инерции вычисляются по формуле (5.9), если в них положить α = α0, или по формулам:
JU = |
Jx + J y |
± |
1 |
(Jx − J y )2 +4Jxy2 |
, |
||
|
2 |
||||||
|
|
2 |
|
|
|
|
|
JV = |
Jx + J y |
|
(Jx − J y )2 +4Jxy2 . |
(5.13) |
|||
|
|||||||
|
|
2 |
|
|
|
|
|
50
