Сопротивление материалов конспект лекций

рицательным. Касательное напряжение принимается положительным, если его для совмещения с направлением внешней нормали к площадке необходимо повернуть на 90° против хода часовой стрелки, обратное направление касательного напряжения считается отрицательным.

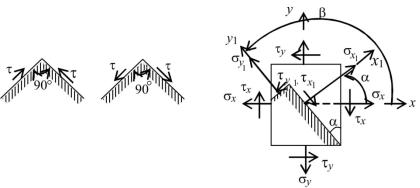
Угол α между осями x и x1 считается положительным (см. рис. 4.2), если внешнюю нормаль к площадке, по которой действует напряжение σх, для совмещения с нормалью к площадке, где действует напряжение σх1, следует повернуть против часовой стрелки.

Между касательными напряжениями τх и τу, действующими на двух взаимно перпендикулярных площадках, имеется однозначная связь, выражаемая законом парности касательных напряжений. В соответствии с этим законом касательные напряжения по двум взаимно перпендикулярным площадкам равны по абсолютной величине и обратны по знаку:

Из закона парности касательных напряжений следует, что по двум взаимно перпендикулярным площадкам касательные напряжения направлены либо к линии пересечения этих площадок (рис. 4.3, а), либо от нее (рис. 4.3, б).

31

sin2 α =1−cos 2α, 2

можно записать формулы (4.2) и (4.4) в иной форме:

Нормальные напряжения, действующие на главных площадках, называются главными напряжениями. Главные напряжения являются экстремальными, т.е. одно главное напряжение имеет наибольшее, другое – наименьшее из возможных значений нормальных напряжений на множестве площадок, проходящих через исследуемую точку.

Определяются главные напряжения по формулам (4.5) и (4.6), где вместо угла α подставляется угол наклона главных площадок α0.

Вместо формул (4.5) и (4.6) главные напряжения могут определяться по формуле

33

Знаки в формуле (4.9) расставляются таким образом, чтобы удовлетворялись условия: если σx > σy, то σглI > σглII , и наоборот.

При изучении плоского напряженного состояния в точке обычно рассматриваются две задачи:

2. По известным нормальным и касательным напряжениям на произвольных взаимно перпендикулярных площадках необходимо определить главные напряжения и положение главных площадок. Задача решается с помощью формул (4.8) и (4.9). Пример задачи дан на рис. 4.6. Полагаем, что σх > σу.

34

4.4. Объемное напряженное состояние

Наибольшее касательное напряжение действует по площадке, наклоненной под углом 45° к главным напряжениям σ1 и σ3 и па-

раллельной главному напряжению σ2 :

τmax = σ1 – σ3 .

2

Деформации при объемном напряженном состоянии

Рассмотрим деформацию бесконечно малого элемента с размерами ребер dx, dy, dz (рис. 4.7). По граням параллелепипеда действу-

35

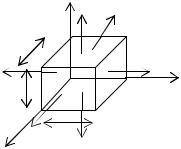
ют главные напряжения σ1, σ2, σ3. Вследствие деформации длины ребер элемента становятся равными dx + ∆dx, dy + ∆dy, dz + ∆dz.

Из формул (4.15) легко можно получить закон Гука для плоского напряженного состояния как частного случая объемного напряженного состояния.

Объемная деформация. При упругой деформации тела изменяется его объем. Относительное изменение объема элементарного параллелепипеда определяется как

где V0 – объем элемента до деформации; V1 – объем элемента в деформированном состоянии.

Выразив главные удлинения через главные напряжения при помощи формул (4.15), получим

36

Потенциальная энергия деформации

Потенциальной энергией деформации называется энергия, которая накапливается в теле при его деформации. В упругой области она численно равна работе внешних сил, затраченной на деформацию тела. Энергия, отнесенная к единице объема, называется удельной потенциальной энергией деформации. При простом растяжении

Распространяя эту формулу на случай объемного напряженного состояния, получим выражение для полной удельной потенциальной энергии:

Рис. 4.8

37

Здесь σср= σ1 +σ32 +σ3 .

Первое напряженное состояние представляет собой всестороннее растяжение либо всестороннее сжатие, т.е. приводит к изменению объема без искажения формы. Второе состояние связано с изменением формы.

В соответствии с этим можно считать, что полная удельная потенциальная энергия деформации состоит из удельной потенциальной энергии изменения объема uоб и удельной потенциальной энергии изменения формы uф:

Удельная потенциальная энергия изменения объема определяется по формуле

Формула для определения удельной потенциальной энергии изменения формы имеет вид

4.5. Теории прочности

Теории прочности предназначены для оценки прочности при сложных напряженных состояниях на основании испытаний, проведенных при простых видах нагруженности, обычно при осевом растяжении.

В зависимости от условий нагружения материал может находится в различных механических состояниях с точки зрения прочности, а именно: состояние упругости, пластичности, разрушения.

Механическое состояние в основном определяется напряженным состоянием.

38

Предельным называется напряженное состояние, при котором происходит качественное изменение механического состояния.

Коэффициент запаса (n) для заданного напряженного состояния – число, на которое надо умножить компоненты напряженного состояния, чтобы было достигнуто предельное напряженное состояние.

Эквивалентное напряжение – напряжение, которое надо создать в растянутом образце, чтобы его напряженное состояние стало равноопасным заданному.

Равноопасными называются напряженные состояния, для которых равны коэффициенты запаса: n = nэ (рис. 4.9).

σ2

σэкв σэкв

Рис. 4.9

Если σэкв достигает предела текучести или предела прочности при одноосном растяжении, то в элементе, находящемся в сложном напряженном состоянии, также начнется течение или разрушение материала. Если же σэкв будет меньше предельного напряжения σпр при одноосном растяжении, то рассматриваемый элемент и образец будут обладать одинаковым запасом прочности

n = σпр . σэкв

В этом случае условие прочности имеет вид

σэкв ≤ [σ], или n ≥ [n].

39

Рассмотрим пять теорий прочности.

Первая теория прочности: теория наибольших нормальных напряжений

Эта теория связывает разрушение материала с достижением наибольшим нормальным напряжением предельного значения. Согласно данной теории напряженные состояния будут равноопасными, если их наибольшие нормальные напряжения одинаковы.

Поскольку при сложном напряженном состоянии наибольшим нормальным напряжением является σ1, условие прочности будет иметь вид

Теория не получила подтверждения в целом ряде экспериментов, однако она иногда применяется при расчете конструкций из очень хрупких материалов (бетон, камень, кирпич).

Вторая теория прочности: теория наибольших относительных удлинений

В этой теории в качестве критерия разрушения принято наибольшее относительное удлинение. Теория утверждает, что напряженные состояния будут равноопасны, если для них равны наибольшие относительные удлинения.

Наибольшее относительное удлинение при трехосном напряженном состоянии согласно обобщенному закону Гука возникает в направлении первого главного напряжения:

При эквивалентном одноосном напряженном состоянии

εmax = σEэкв .

40