
Сопротивление материалов конспект лекций
..pdf
δ |
|
= δ |
|
+ 1+ |
2Н |
(18.5) |
д |
1 |
. |
||||
|
|
ст |
|
|
|
|
|
|
|
|
|
δст |
|
Таким образом, в соответствии с зависимостью (18.2) находим коэффициент динамический:
|
|
|
|
|
|
|
kд =1+ |
1+ |
|
2Н |
. |
(18.6) |
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
δст |
|
|
|
Учитывая, что Н = |
|
υ2 |
(υ – скорость падающего груза в начале |
|||||||||||
|
2g |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
удара), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kд =1+ |
1+ |
|
υ2 |
. |
(18.7) |
||
|
|
|
|
|
|
|
gδст |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку |
2Н |
= |
|
Т |
0 |
, где Т0 |
=QH = |
Qυ2 |
– кинетическая энер- |
|||||
δст |
|
|
|
2g |
||||||||||
|
|
Uст |
|
|
|
|
|
|
||||||
гия падающего груза к моменту соударения; Uст = 12 Qδст −потенци-
альная энергия деформации стержня при статическом приложении нагрузки Q, коэффициент динамичности можно также выразить
формулой
kд =1+ 1+ |
Т0 |
. |
(18.8) |
|
|||
|
Uст |
|
|
Если Н = 0 (внезапный удар), то kд = 2.
Поскольку обычно Н >> δст, то в выражении (18.8) можно пренебречь единицей под корнем, получая следующие формулы:
kд ≈1+ |
2Н |
, |
(18.9) |
|
|||
|
δст |
|
|
181
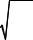
или
k ≈ |
2Н |
. |
(18.10) |
д δст
Учитывая линейную связь между напряжением и деформацией, а также принимая одинаковыми модули упругости при статическом и ударном действии нагрузки, по аналогии с формулой (18.2) можно записать связь между статическим и динамическим напряжениями:
σд = kдσст, |
(18.11) |
где σст – напряжение, возникающее в стержне под действием силы,
равной весу падающего груза. Динамическая нагрузка при ударе
Fд = kдFст. |
(18.12) |
18.2. Горизонтальный удар
Кинетическая энергия движущегося груза
Т0 = |
mυ2 |
(18.13) |
0 . |
||
|
2 |
|
После того как груз коснется ударяемого тела, скорость его начнет уменьшаться. Когда вся кинетическая энергия груза перейдет в потенциальную энергию деформации ударяемого тела, груз остановится, а перемещение δд точки удара будем максимальным. По-
тенциальная энергия деформации
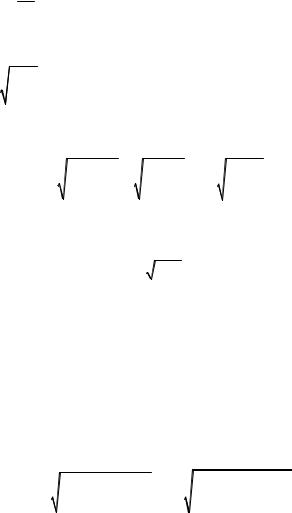
U = |
1 Q δ |
. |
(18.14) |
|
2 д д |
|
|
182
Приравнивая кинетическую энергию движущегося груза к потенциальной энергии деформации ударяемого тела и учитывая, что
Qд = сδд, δд = Qсд , получим
|
mυ2 |
|
1 Q2 |
|
сδ2 |
|
|
|
|
0 |
= |
|
д |
= |
д |
, |
(18.15) |
|
2 |
2 с |
2 |
|||||
|
|
|
|
|
||||
откуда δд = |
mυ2 |
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
Умножив в подкоренном выражении зависимости (18.15) числитель и знаменатель на ускорение свободного падения, получим
δ |
|
= |
m g |
υ2 |
= |
υ2 |
δ |
ст |
= δ |
|
υ2 |
|
|
д |
с g |
0 |
o |
|
ст |
0 |
. |
(18.16) |
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
g |
|
|
g δст |
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
kд = |
υ0 |
|
. |
|
|
|
(18.17) |
|
|
|
|
|
|
gδст |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Формула (18.17) аналогична формуле (18.7).
Динамическое напряжение и динамическая нагрузка определяются по тем же формулам, что и при вертикальном ударе,
σд = kдσст, Fд = kдFст.
18.3.Учет массы ударяемого тела
Сучетом массы ударяемого тела коэффициент динамический может быть записан в следующем виде:
kд = 1+ |
1 |
+ |
2Н |
= 1 |
+ |
1+ |
υ2 |
. (18.18) |
||
δст (1 |
+ α β) |
gδст (1+ α β) |
||||||||
|
|
|
|
|
|
|
||||
β = QQc ,
183

где Qс – вес ударяемого тела (системы); Q – вес ударяющего элемента; α – коэффициент приведения массы ударяемого тела.
Коэффициент α имеет для каждого конкретного случая свое значение, эти коэффициенты приводятся в справочных таблицах по сопротивлению материалов. Так,
–при продольном ударе о стержень постоянного поперечного сечения α = 13 ;
–в случае, когда груз падает на середину двухопорной статиче-
ски определенной балки, α = 1735 ;
– на конце консольной балки α =14033 .
Учет массы ударяемого тела приводит к повышению точности расчета, а соответственно, и к снижению расхода материала, так как коэффициент динамический при учете этого фактора снижается.
18.4. Рекомендации по снижению динамических напряжений при ударе
Снижение напряжений при ударе может быть достигнуто следующими путями:
1)увеличением объема материала подвергаемого удару упругого стержня постоянного сечения;
2)в стержне с выточкой эффект может быть получен за счет уменьшения площади утолщенной части и увеличения тем самым деформативности стержня; этой же цели можно добиться, взяв материал с более низким модулем упругости;
3)увеличением длины стержня;
4)применением буферных пружин, различных податливых прокладок на шарнирно-подвижных опорах.
184
18.5. Ударная вязкость
Ударной вязкостью материала ак называется величина работы разрушения образца, отнесенная к площади его поперечного сечения в месте надреза.
Для оценки способности материала сопротивляться ударным нагрузкам применяют особый вид испытаний ударным изгибом – определение ударной вязкости надрезанных образцов. Эти испытания проводят на маятниковых копрах.
Испытания позволяют оценить особое качество металла – его склонность к хрупкости при динамических нагрузках в условиях сложного напряженного состояния в области надреза и решить вопрос о применимости того или иного материала для данных условий работы. Именно в таких условиях работают многие детали машин, имеющие отверстия, канавки для шпонок и т.д.
На ударную вязкость, например, сталей сильное влияние оказывает температура, структура, химические добавки и другие факторы. При снижении температуры ударная вязкость уменьшается. При этом существует интервал температуры, называемый критическим, когда ударная вязкость снижается особенно быстро. Ударная вязкость сталей с мелкозернистой структурой одной и той же плавки значительно выше, чем у сталей с крупнозернистой структурой.
Ударная хрупкость может появляться и при повышенных температурах. Например, ударная вязкость углеродистых сталей значительно снижается в интервале температур 200–550 °С.
18.6. Примеры расчета на ударные нагрузки
Пример 1
Сравнить динамическое напряжение в стержнях постоянного и переменного сечений (рис. 18.3, а, б). Определить перемещение
сечения А. |
d1 |
= 2, |
l1 |
= 2, Q = 200 Н, h = 10 см, l2 = 40 см, |
|
d2 |
l2 |
||||
|
|
|
[σ] = 160 МПа, d1 = 60 мм.
185

Рис. 18.3
Решение:
σд = σст Kд,
где Kд = 1+ 1+ 2δН , σст = Мизг .
ст W
Для определения σст, δст построим эпюру Мизг от силы Q, действующей статически, а также эпюру изгибающего момента от единичного усилия F = 1, приложенного в сечении соударения груза Q
с рамой (рис. 18.4, а, б).
|
|
|
|
Рис. 18.4 |
|
|
|
|
|
|
Определим |
величину |
статического |
перемещения δст в сече- |
|||||||
нии А: |
|
|
|
|
|
|
|
|
|
|
– для рамы постоянного сечения: |
|
|
|
|
|
|
||||
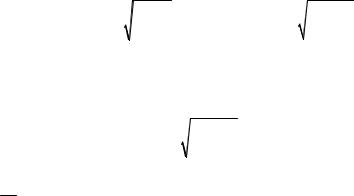
δст |
= |
1 |
1 Ql2l1 2 l2 + Ql2 |
l1 l2 |
+ |
1 Ql2l2 |
2 l2 |
|
, |
|
|
||||||||||
|
|
ЕJ2 2 |
3 |
2 |
|
2 |
3 |
|
|
|
186 |
|
|
|
|
|
|
|
|
|
|
δст = |
|
1 |
|
1 |
200 |
0,8 2 |
0, 4 + 200(0, 4)2 0, 4 + |
1 200(0, 4)3 2 |
|
= |
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
ЕJ2 2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
||||||||
|
|
= |
38, 4 |
= |
|
|
|
|
|
38, 4 64 |
|
|
|
|
= 4,38 10−3 м = 4,83 |
мм; |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
EJ2 |
2 |
|
|
11 |
|
|
4 |
|
|
−8 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
10 3,14 3 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
– для рамы переменного сечения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
δст = |
|
1 |
|
1 Ql2l1 2 l2 + Ql2 |
l1 l2 + |
1 |
|
+ 1 Ql2l2 2 l2 |
|
, |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ЕJ2 2 |
|
3 |
|
|
|
|
|
|
2 |
|
16 2 |
|
|
3 |
|
|
|
|
|
|
||||||||||||
|
δст |
= |
|
|
1 |
|
|
1 |
200 0,8 |
2 0,4 + 200( |
0,4)3 |
1 |
+ |
200(0,4)3 1 |
|
= |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
ЕJ2 2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
= |
26,4 |
= |
|
26,4 64 |
|
|
|
= 3,32 мм. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
EJ2 |
|
11 |
|
|
|
|
|
|
4 |
10 |
−8 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 10 |
3,14 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Динамическое напряжение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
– для рамы постоянного сечения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ql |
|
|
|
|
2h |
|
200 0,4 32 |
|
|
|
|
200 |
|
|
|||||||||||||||
σ |
|
= σ |
|
K |
|
|
= |
|
2 |
1 |
+ |
1+ |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
1+ 1+ |
|
|
|
|
= |
|||||||||
|
|
|
|
|
W |
|
δ |
|
|
3,14 33 10−6 |
4,83 |
|
||||||||||||||||||||||||||||||
|
max |
|
|
|
ст |
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
ст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=226,8 106 Па = 226,8 МПа;
–для рамы переменного сечения:
σmax = |
200 |
0,4 32 |
1+ |
1+ |
200 |
|
= 267 МПа, |
|
|
|
|
|
|
||||
3,14 |
33 10−6 |
3,32 |
|
|||||
|
|
|
|
|
|
|
|
|
σб = 267 =
тогда д 1,18.
σад 226
Увеличение жесткости на участке ВС привело к увеличению динамического напряжения на 18 %.
187

Определим допустимую высоту падения для рамы постоянного сечения:
|
|
σд = σстKд ≤[σ] |
, Kд |
= [σ] , |
|||||
|
|
|
|
|
|
|
σст |
|
|
|
|
1+ |
2h |
= |
[σ] −1 = |
160 |
−1 = |
4,3, |
|
|
|
|
|
||||||
|
|
|
δст |
σст |
30, 2 |
|
|
||
h ≤ |
17,5 δст |
=17,5 4,83 10−3 |
= 4,22 10−3 м = 4,22 см. |
||||||
2 |
|||||||||
|
|
|
|
2 |
|
|
|
||
Коэффициент |
динамический |
Kд =5,3 |
при высоте падения |
||||||
4,22 см.
Вычислим динамическое перемещение сечения А при допустимой высоте падения:
δд = δстKд = 4,83 5,3 = 25,6 мм.
188
СПИСОК ЛИТЕРАТУРЫ
Литература, обязательная для изучения
1.Феодосьев В.И. Сопротивление материалов: учебник. – М.: МГТУ им. Баумана, 1999. – 592 с.
2.Ицкович Г.М. Руководство по решению задач по сопротивлению материалов: учеб. пособие для втузов. – М.: Высшая школа, 2001. – 399 с.
3.Ицкович Г.М. Сопротивление материалов: учебник. – М.: Выс-
шая школа, 2001. – 368 с.
Дополнительная литература
1.Степин П.А. Сопротивление материалов: учебник для немашиностроительных специальностей вузов. – М.: Высшая школа, 1983. – 303 с.
2.Сопротивление материалов: учебное пособие / Н.Н. Вассерман, А.П. Жученков, М.Л. Зинштейн, А.М. Ханов. – 2-е изд., испр. и доп. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2011. – 365 с.
3. Сборник задач по сопротивлению материалов / под ред. А.С. Вольмира. – М.: Наука, 1984. – 408 с.
4.Справочник по сопротивлению материалов / Г.С. Писаренко [и др.]. – Киев: Наукова думка, 1975. – 704 с.
5.Сопротивление материалов: задания к контрольным расчетнопроектировочным работам с учетом специфики модульного обучения для студентов всех специальностей / Перм. гос. техн. ун-т. – Пермь, 1999. – 92 с.
6.Расчет и конструирование валов: метод. указания к курсовой работе по сопротивлению материалов / Перм. гос. техн. ун-т. – Пермь, 1998. – 26 с.
7.Справочные таблицы для выполнения учебных заданий и рас- четно-проектировочных работ по курсу сопротивления материалов / Перм. гос. техн. ун-т. – Пермь, 2009. – 34 с.
8.Механические испытания материалов: лабораторный практикум по курсу «Сопротивление материалов» / Перм. гос. техн. ун-т. – Пермь, 2001. – 16 с.
189
ПРИЛОЖЕНИЕ
Таблица П.1
Нормальные линейные размеры, мм
10 |
18 |
32 |
56 |
100 |
180 |
320 |
560 |
10,5 |
19 |
34/35 |
60/62 |
105 |
190 |
340 |
600 |
11 |
20 |
36 |
63/65 |
210 |
200 |
360 |
630 |
11,5 |
21 |
38 |
67/70 |
120 |
210 |
380 |
670 |
12 |
22 |
40 |
71/72 |
125 |
220 |
400 |
710 |
13 |
24 |
42 |
75 |
130 |
240 |
420 |
750 |
14 |
25 |
45/47 |
80 |
140 |
250 |
450 |
800 |
15 |
26 |
48 |
85 |
150 |
260 |
480 |
850 |
16 |
28 |
50/52 |
90 |
160 |
280 |
500 |
900 |
17 |
30 |
53/55 |
95 |
170 |
300 |
530 |
950 |
Примечание: за косой чертой приведены размеры посадочных мест для подшипников качения.
Таблица П.2 Механические характеристики углеродистых конструкционных сталей
Марка стали |
σв, МПа |
σт, МПа |
τт, МПа |
σи−1, МПа |
σ−р1, МПа |
τк−1, МПа |
10 |
340 |
210 |
140 |
160–220 |
120–150 |
80–120 |
20 |
420 |
250 |
160 |
170–220 |
120–160 |
100–130 |
25 |
460 |
280 |
– |
190–250 |
– |
– |
30 |
500 |
300 |
170 |
200–270 |
170–210 |
110–140 |
35 |
540 |
320 |
190 |
220–300 |
170–220 |
130–180 |
40 |
580 |
340 |
– |
230–320 |
180–240 |
140–190 |
45 |
610 |
360 |
220 |
250–340 |
190–250 |
150–200 |
50 |
640 |
380 |
– |
270–350 |
200–260 |
160–210 |
55 |
660 |
390 |
260 |
290 |
216 |
170 |
60 |
690 |
410 |
– |
310–380 |
220–280 |
180–220 |
20Г |
460 |
280 |
– |
– |
– |
– |
30Г |
550 |
320 |
– |
220–320 |
– |
– |
50Г |
660 |
400 |
– |
290–360 |
– |
– |
20Х |
800 |
650 |
– |
380 |
– |
170–230 |
40Х |
1000 |
800 |
– |
350–380 |
250 |
225 |
45Х |
1050 |
850 |
– |
400–500 |
– |
– |
30ХМ |
950 |
750 |
– |
310–410 |
370 |
230 |
190
