Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

Диэлектрики. В диэлектриках внешнее электрическое поле не в состоянии создать направленное движение электронов, так как они все находятся в валентных подоболочках своих атомов. Это означает, что в валентной зоне свободных уровней энергии нет (рис. 24.4б), а «перепрыгнуть» в зону проводимости у электронов энергии не хватает. В терминах зонной теории

Диэлектриками называются твердые тела с заполненной электронами валентной зоной и шириной запрещенной зоны более 5 эВ.

Полупроводники. При температуре равной абсолютному нулю полупроводники электрический ток не проводят. При их нагревании внешнее электрическое поле создает слабый ток, величина которого возрастает с увеличение температуры. С точки зрения зонной теории

Полупроводниками называются твердые тела с заполненной электронами валентной зоной и шириной запрещенной зоны от 0,1 до 5 эВ.

При этом полупроводники с шириной запрещенной зоны от 0,1 до 3 эВ называют узкозонными полупроводниками, а с шириной запрещенной зоны от 3 до 5 эВ – широкозонными полупроводниками.

Если температура полупроводника отлична от нуля, то некоторые быстрые электроны, энергия которых превышает ширину запрещенной зоны, могут оторваться от своих атомов и переместиться в зону проводимости. Образуются сразу пары свободных носителей заряда (рис. 24.4в): электроны в зоне проводимости и дырки (разрывы валентных связей в местах ушедших электронов) в валентной зоне. С ростом температуры концентрация таких носителей возрастает, и электропроводность полупроводника увеличивается.

Полуметаллы. Если ширина запрещенной зоны равна нулю (рис. 24.4г), то она сливается в зонной проводимости, и твердое тело,

302

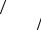
фактически, становится металлом, так как теперь для электронов появляется возможность занимать вышележащие уровни энергии и участвовать в протекании электрического тока. Такие металлы принято называть полуметаллами.

Поскольку уровень Ферми определяет среднюю энергию электронов, то у металлов он находится в разрешенной зоне (она же зона проводимости), а у полупроводников и диэлектриков – в запрещенной зоне.

§ 3. Электропроводность металлов

Как уже отмечалось в § 1 настоящей лекции, электронный газ в металлах является вырожденным, и для его описания необходимо пользоваться статистикой Ферми – Дирака (24.1). Она характеризует вероятность заполнения электронами имеющихся квантовых состояний. Число же самих этих состояний в единице объема металла, приходящихся на единичный интервал энергии – плотность электронных состояний – описывается другой функцией распределения:

Число электронов в единице объема с энергией от E до E + dE с учетом того обстоятельства, что в одном состоянии могут находиться два электрона с противоположными спинами, тогда можно найти как

Отсюда концентрация электронов, имеющих энергию в интервале от E1 до E2 , найдется в виде интеграла

303

Полагая E1 = 0, а E2 → ∞, из записанного выражения можно получить концентрация свободных электронов в металле:

Из (24.5) легко выразить энергию Ферми в металле, если для н е- го известна концентрация свободных электронов:

На рис. 24.5 представлены графики распределения по энергиям плотности электронных состояний и концентрации свободных электронов, приходящейся на единичный интервал энергии.

Рис. 24.5. Графики зависимости от энергии плотности электронных состояний

и концентрации самих электронов

304

Из приведенных графиков видно, что увеличить свою энергию во внешнем электрическом поле и участвовать в протекании электрического тока может лишь небольшая часть электронов, находящихся вблизи уровня Ферми, поскольку все низлежащие состояния заняты.

С ростом температуры количество таких электронов увеличивается пропорционально температуре кристалла, а поскольку электроны, в действительности, являются волнами де Бройля, то увеличивается также пропорционально температуре вероятность их рассеяния на фононах. Это объясняет прямо пропорциональную зависимость удельного сопротивления металлов от температуры, которую не могла объяснить классическая теория электропроводности Друде – Лоренца (см. § 3 лекции 6).

Квантовые представления об электропроводности металлов позволили объяснить также явление сверхпроводимости, открытое еще в 1911 г. нидерландским физиком Г. Камерлинг-Оннесом. Квантовая теория сверхпроводимости, построенная американскими физиками Дж. Бардиным, Л. Купером и Дж. Шриффером 1957 г., показывает, что при температурах ниже так называемой критической температуры (T < Tс )в результате обмена фононами происходит спаривание элек-

тронов. В таких электронных парах фононы отбирают энергию у одного электрона и передают ее другому. В результате энергия электронов не изменяется при рассеянии на фононах, и сопротивление металла обращается в нуль.

В металлах и их сплавах критическая температура, при которой наступает сверхпроводимость, невелика. Например, в сплаве Nb3Sn Tc =18,2К. В последнее время на основе медь-содержащих керамик созданы высокотемпературные сверхпроводники, в которых критическая температура превышает 100 К. Одним из таких материалов является керамика HgBa2Ca2Cu3O8+x, у которой Tc =135К.

305

§ 4. Электропроводность полупроводников

Собственная проводимость. Структура энергетических зон в собственных (чистых, без примесей) полупроводниках была показана на рис. 24.4в. В таких полупроводниках имеется два типа носителей заряда: электроны в зоне проводимости и дырки в валентной зоне. Соответственно, плотность создаваемого ими электрического тока

где индекс «е» относится к электронам (от англ. electrons – электроны), а индекс «h» – к дыркам (от англ. holes – дырки). Концентрация и тех, и других в собственных полупроводниках одинакова:

и обозначена ni (от англ. intrinsic conduction – собственная проводимость). Скорости дрейфа соответствующих носителей заряда обозначены как ve и vh .

В собственных полупроводниках уровень Ферми располагается приблизительно посередине запрещенной зоны, ширина которой существенно превышает значения тепловой энергии носителей при температурах, близких к комнатным. Поэтому E − EF ≈ Eg 2 kT , и

распределение Ферми – Дирака (24.1) принимает вид распределения Больцмана:

Из (24.9) следует, что концентрация носителей заряда также удовлетворяет распределению Больцмана:

306

где значение n0 соответствует T → ∞. Поскольку в выражении (24.7) скорости дрейфа электронов и дырок слабо зависят от температуры, то, переходя к подвижностям носителей заряда µe = ve E, µh = vh E, где E – напряженность приложенного электрического поля, можем записать его в виде

j = en0 (µe + µh )e−Eg 2kT E.

Сравнивая эту запись с законом Ома в дифференциальной форме ( j =σE ), получаем зависимость удельной проводимости для собственных полупроводников в виде

где σ0 = en0 (µe + µh ) – значение коэффициента электропроводности при T → ∞.

307

проводников с увеличением температуры обусловлено ростом концентрации свободных носителей заряда (электронов и дырок). Этим обстоятельством полупроводники принципиально отличаются от металлов, электропроводность которых с увеличением температуры уменьшается.

Примесная проводимость. Различают примесные полупроводники n -типа и p -типа.

В полупроводниках n -типа атомы примеси имеют более высокую валентность, чем собственные атомы. Например, это могут быть атомы пятивалентного фосфора (P) в кристаллической решетке из атомов четырехвалентного кремния (Si). Четыре валентных электрона фосфора образуют совместно с четырьмя валентными электронами кремния прочные ковалентные связи, а «лишний» пятый электрон может легко оторваться от своего атома и перейти в зону проводимости, если ему сообщить энергию ионизации ∆Ed = Ec − Ed (рис. 24.7а). Примесь, создающая в полупроводнике избыточные электроны, называется донорной примесью. Атомы донорной примеси подбирают таким образом, чтобы занимаемые ими уровни энергии располагались в запрещенной зоне полупроводника вблизи дна зоны проводимости.

В полупроводниках p -типа атомы примеси имеют меньшую валентность, чем собственные атомы. В кристаллической решетке из атомов кремния это могут быть, например, атомы трехвалентного бора (B). Для образования четвертой ковалентной связи с окружающими соседними атомами кремния у атома бора не хватает одного валентного электрона. Такая разорванная связь называется дыркой (рис. 24.7а). Но эта связь может быть восстановлена путем захвата недостающего электрона из валентной подоболочки какого-либо соседнего атома кремния. При этом атом кремния, лишившийся электрона, превращается в отрицательный ион, а в его разорванной валентной подоболочке образуется дырка. Примесь, захватывающая

308

электроны для образования химических связей с окружающими атомами полупроводника, называется акцепторной примесью (от англ. accept – захватывать). Энергия ионизации акцепторных атомов равна ∆Ea = Ea − Ev . Атомы акцепторной примеси стараются подбирать таким образом, чтобы занимаемые ими уровни энергии располагались в запрещенной зоне полупроводника вблизи потолка валентной зоны.

Рис. 24.7. Примесные атомы (а) и структура энергетических зон (б) в случае

полупроводников n-типа (вверху) и р-типа (внизу)

309

На рис. 24.7б показаны зонные диаграммы для примесных полупроводников n-типа и р-типа. Поскольку энергия ионизации примесных атомов намного меньше, чем ширина запрещенной зоны, то ясно, что при температурах, близких к комнатным, концентрация электронов n в полупроводниках n-типа значительно превышает концентрацию дырок p :

n ≈ nd p ≈ ni ,

а концентрация дырок в полупроводниках р-типа значительно превышает концентрацию электронов:

p ≈ na n ≈ ni .

Здесь nd и na – соответственно концентрации донорных и акцепторных атомов, а ni – концентрация собственных носителей заряда – электронов и дырок, обусловливающих собственную проводимость полупроводника.

В полупроводниках n-типа основными носителями заряда явля-

В полупроводниках р-типа основными носителями заряда являются дырки, и плотность создаваемого ими тока

Температурная зависимость примесной проводимости находится так же, как и в случае собственной проводимости, и описывается похожей формулой

310