Частные случаи движения точки

Равномерное движение. При равномерном движении точки по траектории любой формы , следовательно, постоянна и алгебраическая скорость , которая может отличаться от только знаком. Так как

, то , ,

если принять при .

Равнопеременное движение. Равнопеременным движением называют такое движение по траектории любой формы, при котором касательное ускорение . Движение является равноускоренным, если алгебраическая скорость и касательное ускорение имеют одинаковые знаки. Если и , имеют разные знаки, то движение является равнозамедленным.

Получим формулы для алгебраической скорости и расстояния при равнопеременном движении. Имеем

, , ,

следовательно , (21)

если принять при .

Так как , то с учетом (21)

, ,

если при .

Выполняя интегрирование, получим:

. (22)

Из (21) и (22) можно определить любые две неизвестные величины, если известны остальные три величины, входящие в эти формулы.

1.6. Скорость и ускорение точки в полярных координатах

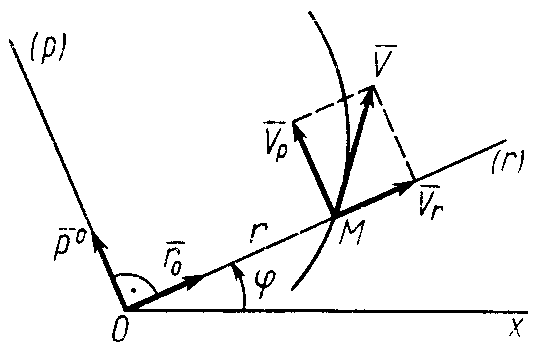
Рассмотрим движение точки по плоскости. В этом случае движение можно задать в полярных координатах. Для этого примем какую-либо точку плоскости за полюс и проведем из нее полярную ось, например ось (рис. 20). Положение движущейся точки на плоскости известно, если заданы радиус-вектор и полярный угол как функции времени, т.е.

, . (23)

П

Рис. 20

олярный угол считается положительным, если он откладывается от полярной оси до радиуса-вектора против часовой стрелки. Радиус-вектор как расстояние от точки до точки принимает только положительные значения.

Уравнения (23) называются уравнениями движения точки в полярных координатах. Они являются также уравнениями траектории точки в параметрической форме. Если из (23) исключить параметр – время , то получим уравнение траектории в полярных координатах:

.

Введем единичный вектор , направленный по радиусу-вектору от полюса к точке . Тогда

.

Для скорости получаем:

.

Согласно (15), для производной по времени от единичного вектора имеем:

,

где вместо единичного вектора введен единичный вектор , направление которого получается поворотом вектора на 90⁰ в положительном направлении угла , т.е. против часовой стрелки (рис. 20). После этого для скорости точки получаем:

. (24)

Это разложение скорости точки на радиальную и трансверсальную (поперечную) составляющие, т.е.:

, (25)

где , .

Для проекций скорости на оси, положительные направления которых совпадают с направлениями единичных векторов и из (24), получаем:

, . (26)

Они соответственно называются радиальной и трансверсальной скоростями. В зависимости от знаков производных и радиальная и трансверсальная скорости могут быть как положительными, так и отрицательными.

Используя (24), определяем ускорение точки в полярных координатах. Имеем

.

Выполняя дифференцирование, получим

.

Для производной по времени от единичного вектора имеем

,

так как вектор поворачивается с той же угловой скоростью , что и вектор , а единичным вектором, по которому направлен вектор , является вектор .

После подстановки в выражение для ускорения производных от единичных векторов и объединения слагаемых имеем

. (27)

Получили разложение ускорения точки на радиальную , и трансверсальную составляющие, т.е.

, , .

Для проекций ускорения на оси и получаем

, . (28)

Ускорение называется радиальным, а – трансверсальным. Трансверсальное ускорение можно выразить также в форме:

.

Это выражение для трансверсального ускорения широко используется при рассмотрении движения планет и искусственных спутников Земли.

Радиальная и трансверсальная составляющие ускорения взаимно перпендикулярны, поэтому

. (29)

Отметим, что для неподвижных осей координат , и справедливы формулы

, , .

Для подвижных осей и , как следует из (26) и (28), и не равны производным по времени от и .

Частные случаи

1. Если , то имеем прямолинейное движение по прямой . В этом случае и , из (26) и (28) получаем:

, , ,

, , .

Эти величины совпадают с ранее полученными в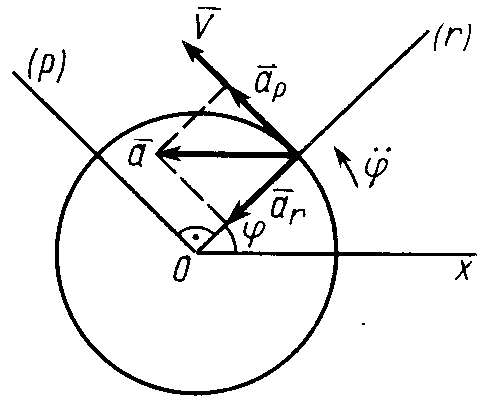 ыражениями для них при изучении движения точки в декартовых координатах. Только расстояние следует заменить на координату .

2

Рис. 21

. При (рис. 23) получаем движение точки по окружности. В этом случае , . Из (26) и (28) имеем:

, , ,

, , .

В этих формулах является угловой скоростью вращения радиуса-вектора, а – его угловым ускорением.