Скорость точки в криволинейных координатах

При движении точки ее радиус-вектор через обобщенные координаты зависит от времени, т.е.

.

По определению скорости и правилу дифференцирования сложных функций имеем

, (39)

где называется обобщенной скоростью точки. Используя (36), из (39) получаем

. (40)

Получено разложение скорости по осям, направление которых совпадает с направлением базисных векторов.

Для величин составляющих скорости по базисным векторам из (40) имеем

. (40')

В случае ортогональности базисных векторов по формуле (40') вычисляются проекции вектора скорости на оси, направленные по базисным векторам. В этом случае для квадрата скорости получаем

.

Ускорение в ортогональных криволинейных координатах

Криволинейные координаты считаются ортогональными, если ортогональны их базисные векторы. В приложениях обычно встречается этот случай. Для ортогональных базисных векторов проекции ускорения точки на их направления вычисляем по формулам

. (41)

Выражая базисные векторы по (36), из (41) получим

. (42)

Для дальнейших преобразований (42) следует воспользоваться тождествами:

, (43)

или , (44)

или . (45)

Тождество (43) . представляет собой известное правило дифференцирования скалярного произведения двух векторов. Докажем справедливость тождеств Лагранжа (44) и (45).

Тождество (44) получим из (39) дифференцированием , например, по . Учитывая, что производные с не могут зависеть от , имеем:

.

Аналогично

, .

т. е.

.

Справедливость тождества (44) установлена.

Для доказательства тождества (45) продифференцируем из (39) по . Получим:

. (46)

Учитывая, что не может зависеть от обобщенных скоростей, и дифференцируя ее по времени как сложную функцию времени, имеем:

. (47)

Правые части (46) и (47) совпадают, так как они отличаются только порядком частного дифференцирования, от которого частные производные не зависят. Следовательно, тождество (45) доказано. Используя тождества, преобразуем выражение в скобках из (42). Получим

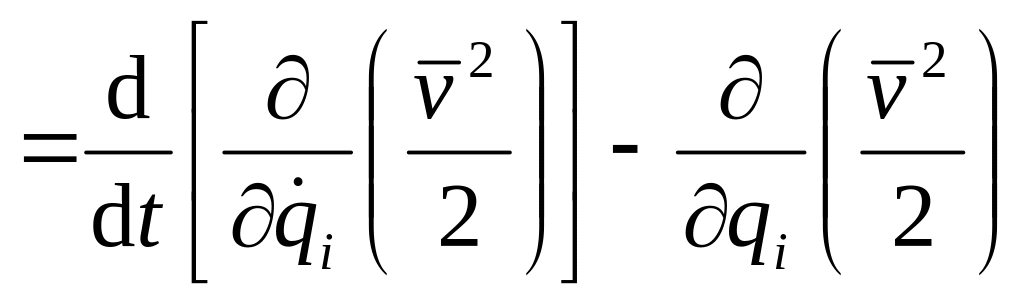. (48)

Учитывая, что , и вводя функцию , из (42) с учетом (48) имеем:

. (49)

По формулам (49) можно вычислить проекции ускорения точки на оси, направленные по базисным ортогональным векторам.

1.9. Скорость и ускорение точки в сферических координатах

В

Рис. 23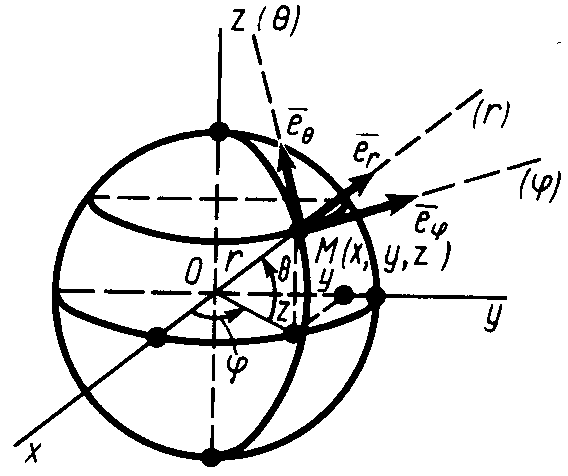

качестве примера использования полученных формул вычислим скорость и ускорение точки в сферических координатах. Сферическими координатами точки являются величины (рис. 23). Координатной линией для является прямая с базисным вектором . Координатной линией для служит параллель сферы с базисным вектором и координатной линией для – меридиан сферы с базисным вектором .

Базисные векторы оказались ортогональными. Декартовы координаты точки через сферические выражаются следующими зависимостями:

, , . (50)

По формулам (38) вычисляем коэффициенты Ламэ. Имеем:

,

,

,

.

Проекции скорости на оси, направленные по базисным векторам, определяем согласно (40'). Получаем:

, , . (51)

Т.к. , то для квадрата скорости и функции имеем:

Проекции ускорения на оси, направленные по базисным векторам, вычисляем по формулам (49). Имеем:

.

. (52)

Для вектора ускорения получаем

Модуль ускорения будет иметь следующее выражение:

Аналогично можно вычислить ранее полученные скорость и ускорение точки в цилиндрических координатах.