3.9. Основные способы вычисления углового ускорения при плоском движении

При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.

1. Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение определяем путем дифференцирования их по времени, т. е.

.

2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным в этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (79):

,

где – точка плоской фигуры; – мгновенный центр скоростей. Дифференцируя по времени, получаем:

_.

В тех случаях, когда постоянно,

_{, (92)}

так как

, ,

где – касательное ускорение точки .

Так, например, при качении колеса без скольжения по неподвижной прямой линии, если за точку взять центр колеса , то, учитывая, что он движется прямолинейно, получим:

,

так как в этом случае

, ,

где – радиус колеса.

При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью подвижного колеса и угловой скоростью кривошипа (рис. 49). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес, получаем

, (93)

г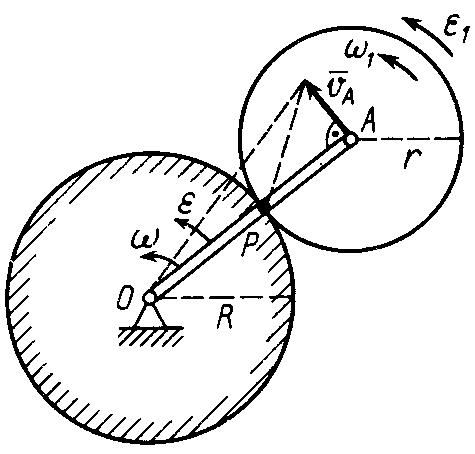 де –радиус неподвижного колеса, – радиус подвижного колеса.

Дифференцируя по времени (93), имеем

, (94)

т. к. , .

И

Рис. 49

з сравнения (93) и (94) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.

При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа .

При внутреннем зацеплении колес дуговые стрелки и , колеса и кривошипа имеют противоположные направления.

3. Иногда угловое ускорение можно найти путем проецирования на оси координат известного по направлению ускорения, например точки , если ускорение какой-либо другой точки и угловая скорость фигуры известны или их можно вычислить предварительно. Так, если ускорение точки

, (95)

то, проецируя обе части (95) на ось , перпендикулярную ускорению , получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.

3.10. Теорема о конечном перемещении плоской фигуры

П

Рис. 50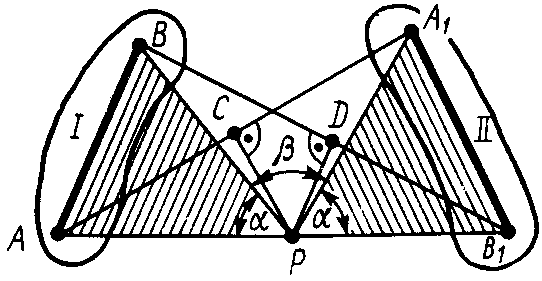

онятие мгновенного центра скоростей плоской фигуры при плоском движении можно ввести используя теорему о конечном перемещении плоской фигуры. Фигуру в ее плоскости из заданного положения I в любое другое положение II (рис. 50) можно перевести одним поворотом в этой плоскости вокруг точки , называемой центром конечного вращения.

Пусть в положении I плоская фигура характеризуется отрезком , скрепленным с фигурой, а в положении II этот отрезок займет положение .

Рассмотрим случай, когда и не параллельны. Можно доказать, что центр конечного вращения находится на пересечении перпендикуляров и , восставленных из середин отрезков и . Для этого докажем, что заштрихованные треугольники и равны по трем сторонам; как гипотенузы в равных прямоугольных треугольниках и , так как по построению точка есть середина отрезка , а – общий катет треугольников. Аналогично, рассматривая равные треугольники и , получаем ; – по условию.

Для перевода плоской фигуры из положения I в положение II достаточно совместить между собой равные треугольники и . Это можно осуществить одним поворотом треугольника в его плоскости вокруг вершины . При этом если сторону до совмещения со стороной повернуть на угол , то сторону до совмещения со стороной следует повернуть на угол , равный углу , так как углы и состоят из общего для них угла и одинаковых углов , лежащих в равных заштрихованных треугольниках против равных сторон.

Итак, если отрезок повернуть вокруг на угол , то отрезок при этом повернется на тот же угол и в том же направлении, что и отрезок , и, следовательно, точка совпадает с точкой , а точка – с точкой , т. е. отрезок совпадет всеми своими точками с отрезком .

В том случае, когда отрезок параллелен отрезку , перпендикуляры к и к параллельны и, следовательно, пересекаются в бесконечности. В этом случае следует считать находящимся в бесконечности и плоскую фигуру из положения I в положение II можно перевести поступательным перемещением, что соответствует повороту фигуры вокруг бесконечно удаленной точки.