2.2. Распределение молекул по скоростям

Беспорядочное движение молекул в газах даёт возможность при их исследовании пользоваться статистиче- скими методами.

Пусть скорости dN молекул попадают в интервал от  до +d. Доля молекул, имеющих скорость в указанном интервале, по отношению к общему числу молекул равна вероятности P того, что молекулы имеют скорость (  +d):

.

Вероятность P, отнесённая к ширине интервала d, называется плотностью вероятности f(): .

Зависимость плотности вероятности (доли) случайной величины от её значения называется функцией распределе- ния этой случайной величины.

Функция распределения скоростей молекул газа была получена Максвеллом и имеет следующий вид:

(2.6)

Здесь N-общее число молекул, m-масса отдельной молекулы. Тогда число молекул, скорости которых заключены в пределах от  до +d, определяется выражением

. (2.7)

График функции f(v) представлен на рис. 2.1.

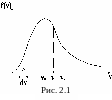
Площадь заштрихованного участка равна доле молекул, скорости которых лежат в интервале от  до +d. Площадь под всей кривой равна доле молекул, скорости которых лежат в интервале от 0 до , а это все молекулы, поэтому такая площадь равна 1:

.

Максвелловское распределение не меняется во времени, оно стационарно. Для данного газа оно зависит только от абсолютной температуры. На рис.2.2 приведены функции распределения скоростей для двух различных температур T₁ и T₂ (T₂T₁).

Рис. 2.2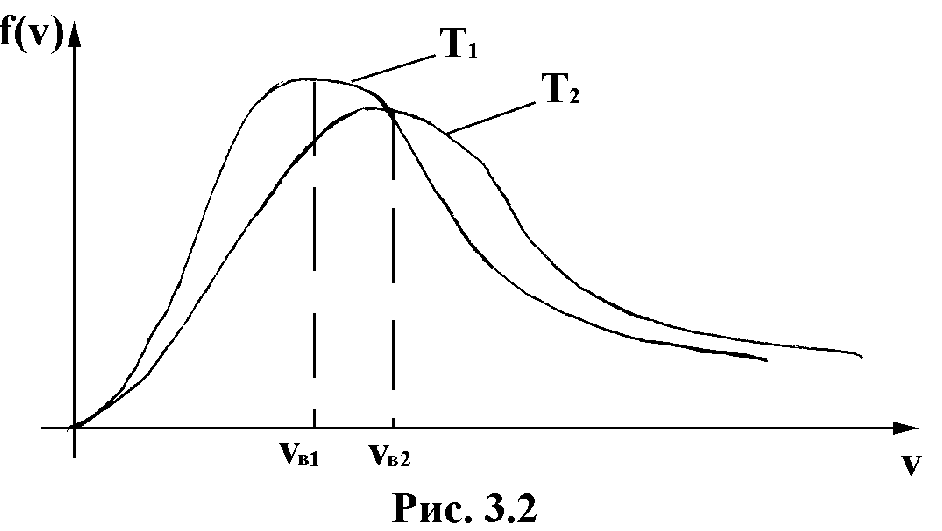

С ростом температуры увеличивается доля молекул, имеющих большую скорость. Скорость при которой функция f(v) достигает максимума называется наиболее вероятной скоростью. Этой и близкой к ней скоростью обладает наибольшее число молекул. Значение наиболее вероятной скорости можно найти из условия .

, (2.8)

где m - масса молекулы, М - молярная масса.

Наряду с наиболее вероятной скоростью в молекулярно-кинетической теории пользуются понятием средней арифметической и средней квадратичной скоростью.

Средняя арифметическая скорость молекул газа

. (2.9)

Эта скорость не совпадает с наиболее вероятной (рис. 2.1), т. к. функция распределения скоростей несимметрична.

Средняя квадратичная скорость молекул газа

. (2.10)

Она совпадает со значением, найденным из уравнения

2.3. Идеальный газ в поле сил тяжести. Распределение Больцмана

Если идеальный газ находится в поле тяжести, то на каждую молекулу действует сила . Выделим в газе элементарный объём dV высотой dh с единичной площадью основания. Условие равновесия этого объёма:

Р₁=Р₂+ nmgdh,

где Р₂-давление у верхнего основания объёма dV, P₁-у нижнего, m-масса молекулы газа, n-концентрация молекул. Отсюда dP = P₂ - P₁ = -nmgdh . Согласно уравнению (2.2) dP =kTdn. Тогда

k T dn= - n m g dh . (2.11)

Решение дифференциального уравнения (2.11) имеет вид:

. (2.12)

Эта функция называется функцией распределения Больцмана и характеризует зависимость концентрации молекул от высоты для случая, когда молекулы находятся в поле тяжести (т. е. от их потенциальной энергии). При этом начальный уровень h =0 может быть выбран произвольно. Воспользовавшись уравнением (2.2), получим зависимость давления от высоты (барометрическую формулу):

. (2.13)