
Дифференциальная геометрия. Приложения к механике. Зайцева М.И., Макаров В.Н
.pdfМ.И. Зайцева, В.Н. Макаров
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ. ПРИЛОЖЕНИЯ К МЕХАНИКЕ
Учебное пособие
Воронеж 2004
3

ВВЕДЕНИЕ
Мы встречались с геометрией уже несколько раз, начиная со средней школы. Школьная геометрия изучает различные метрические свойства простейших геометрических фигур. В основном, находились соотношения между длинами сторон и углами треугольников многоугольников. Иногда вычислялись на базе этого площади, поверхности и объемы некоторых тел.
Центральными понятиями, на которых строилась геометрия, были: длина отрезка на прямой или кривой (длина окружности), а также угол между двумя пересекающимися линиями
– прямыми или кривыми.
Основной целью аналитической геометрии является описание геометрических фигур при помощи уравнений в декартовой системе координат на плоскости или в трехмерном пространстве. Например, эллипс на плоскости описывается уравнением:
x2 |
|
y2 |
1 |
a2 |
|
b2 |
|
|
|
Таким образом, аналитическая геометрия использует метод координат, но предмет геометрии остается тем же, что и в школе.
Также и дифференциальная геометрия – ее предмет остается прежним, но дополнительно в ней используются средства как аналитической геометрии, так и дифференциального исчисления и линейной алгебры.
1. Вектор-функция скалярного аргумента.
1.1. Определение.
Во многих задачах приходиться рассматривать переменные векторы, т.е. векторы, у которых изменена или длина или направление, или и то другое одновременно.
4
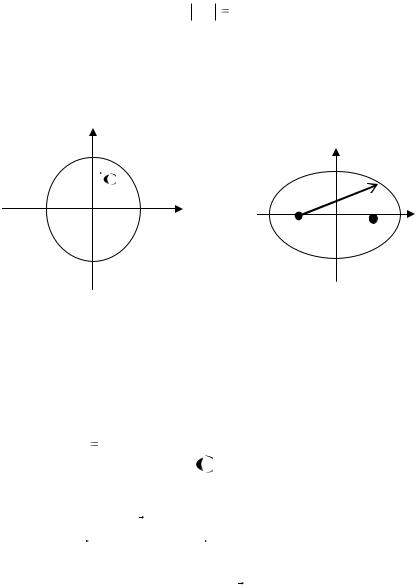
Пример 1. Радиус – вектор точки, движущейся по окружности (рис. 1а). При этом
r(t) const ,
но изменяется направление.
Пример 2 Радиус – вектор точки, движущейся по эллипсу (рис. 1б). В этом радиус – вектор изменяет как длину, так и направление.
y
|
|
y |
|
|
М |
|
|
|
r t |
|
|
|
|
r(t) |
|
0 |
x |
0 |
|
|
|
x |
|
|
|
|
а) |
б) |
|
Рис.1. |
Определение. Если каждому значению скалярной величины t из некоторого множества T поставлен в соответствие
определенный вектор |
|
из некоторого множества векторов R , |
||||
r |
||||||
то говорят, |
что вектор |
|
есть векторная функция скалярного |
|||
r |
||||||
|
|
|
|
|
|
|
аргумента r |
r (t) . |
|
|
|
|
|
Если начало вектора |
совместить с началом системы |
|||||
r t |
||||||
координат, то при изменении t конец радиус-вектора опишет некоторую кривую, которая называется годографом (рис.2).
Радиус-вектор r точки Р, движущейся в пространстве, ее
скорость V , ускорение W являются, очевидно, векторфункциями времени t (рис.3).
Годографом радиус-вектора r движущейся точки будет траектории этой точки.
5

z |
z |
|
|
|
V |
|
r t |
|
k0 |
|
|
r |
|
W |
|
y |
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
i |
x |
Рис.3 |
|
||
x |
Рис.2 |
|
||||
|
|
|
|
|
|
|
В декартовой системе координат всякий вектор можно выразить через его проекции на оси координат. Тогда для r t :
|
|
|
|
(1.1) |
r t |
x t i |
y t j |
z t k |
т.е. его координаты в общем случает являются функциями от t.
x x t , y y t , z z t . |
(1.2) |
1.2. Операции над вектор-функциями
Говорят, что вектор-функция имеет конечный предел, непрерывна, дифференцируема или интегрируема, если соответственно имеют конечные пределы, непрерывны, дифференцируемы или интегрируемы функции……
При этом полагают:
I. |
|
|
|
|
|
|
|
|
||||
limr t |
lim x t |
i |
|
lim y t j |
lim z t k , |
|||||||
|
t |
a |
|
t a |
|
|
|
t a |
t a |
|||
где a обозначает число, |
, |
|
, или |
. |
||||||||
|
|
|
dx |
|
dy |
dz |
|
|
|
|||
II. |
dr |
|
|
- первая производная; |
||||||||
|
|
|
i |
|
|
j |
|
|
k |
|||
|
|
|
|
|
||||||||
|
dt |
|
dt |
|
dt |
dt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
6 |
|

|
|
|
|
d 2 y |
|
d 2r d 2 x |
|||||
|
|
|
i |
|
j |
dt2 |
|
dt2 |
dt2 |
||
|
|
|
|||
r
в других обозначениях:
r
d 2 z |
- вторая производная и т.д. |
||||
|
k |
||||
dt2 |
|||||
|
|
|
|
||
|
|
|
|||
xi |
yj |
zk |
и т.д |
||
|
|
|
|
||
xi |
yj |
zk |
|
||
III. dr d 2r
ка и т.д.
IV. rdt
V.rdt
|
|
|
- дифференциал первого порядка. |
|
dxi |
dyj |
dzk |
||
|
|
|
|
|
d 2 xi |
d 2 yj |
|
d 2 zk - дифференциал второго поряд- |
|
|
|
|
|
|
xdti |
ydtj |
|
zdtk - неопределенный интеграл. |
|
|
|
|
|
|
xdti |
ydtj |
|
zdtk - определенный интеграл |
|
(возможны бесконечные пределы).
1.3. Свойства пределов для вектор-функций
Для пределов вектор-функций справедливы следующие свойства:
1. |
lim |
|
r |
|
|
|
lim r |
|
|
|
|
|
||
|
t |
a |
|
|
|
|
|
t |
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
lim r |
r , если r |
const |
|
||||||||||
|
t |
a |
|
|
|
|
|
|
|
|
||||
3. |
lim kr |
|
k lim r , если k |
const ; |
||||||||||
|
t |
a |
|
|
t a |
|
|
|
|
|||||
4. |
lim ur |
|
lim U lim r; |
U |
U t ; |
|||||||||
|
t |
a |
|
t |
a |
t a |
|
|
||||||
5. |
lim r1 |
r2 |
lim r1 |
lim r2 ; |
|
|||||||||
|
t |
a |
|
|
t |
a |
t |
a |
|
|||||
6. |
lim r1r2 |
|
lim r1 lim r2 ; |
|
||||||||||
|
t |
a |
|
t |
a |
t |
a |
|
|
|||||
7. |
lim r1 |
r2 |
lim r1 |
lim r2 ; |
|
|||||||||
|
t |
a |
|
|
t |
a |
t |
a |
|
|||||
Докажем 1.
7

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
r |
|
lim |
|
|
x2 |
|
y2 |
z2 |
|
|
|
|
|
|
lim x |
|
|
lim y |
|
|
|
lim z |
|
|
lim r |
||||||||||||
t a |
|
|
t a |
|
|
|
|
|
|
|
|
|
|
|
|
|
t a |
|
|
|
|
t a |
|
|
|
t a |
|
|
t a |
|||||||||
что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Докажем равенство 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть r1 |
x1i |
|
y1 j |
z1k , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
r2 |
|
x2 i y2 j z2 k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда |
|
|
|
|
|
i |
j |
|
k |
|
|
|
y |
|
|
z |
|
|
|
z |
|
x |
|
|
|
x |
y |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
r r |
|
x |
y |
|
z |
|
|
|
1 |
|
|
1 |
|
i |
|
1 |
1 |
|
j |
|
1 |
1 |
|
k , |
||||||||||||||
|
|
|
1 |
2 |
|
|
|
1 |
1 |
1 |
|
|
|
y2 |
|
|
z2 |
|
|
|
z2 |
|
x2 |
|
|
|
x2 |
y2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
x2 |
y2 |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
переходя к пределу получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
lim r |
r |
|
lim y1 |
lim z1 |
|
i |
|
lim z1 |
lim x1 |
|
j |
|
lim x1 |
|
lim y1 |
|
k |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
t a 1 |
2 |
|
lim y |
2 |
lim z |
2 |
|
|
|
|
lim z |
2 |
lim x |
2 |
|
|
|
lim x |
|
lim y |
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
lim x1 |
lim y1 |
lim z1 |
|
lim r1 |
|
|
lim r2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
lim x2 |
lim y2 |
lim z2 |
|
t |
|
a |
|
|
t |
a |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Замечания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Вектор r t |
называется бесконечно малым при t |
|
|
a , |
|||||||||||||||||||||||||||||||||
|
|
|
если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lim r |
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.3) |
|||||||
|
|
|
|
|
|
|
|
|
t |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. если lim r |
|
0i |
0 j |
|
|
|
0k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ta
Всилу свойства 1 из равенства (3) следует, что
8

lim r 0 . |
(1.4) |
ta
Вданном случае справедливо и обратное утверждение: из
(1.4) следует (1.3).
lim x2 y2 z2 0 x 0, y 0, z 0 при t a
t a
и, следовательно в силу I справедливо (3). Таким образом равенство (1.3) эквивалентно равенству (1.4).
2. Рассмотрим теперь равенство
lim r |
R |
|
(1.5) |
t a |
|
|
|
Оно эквивалентно равенству: |
|
||
lim r |
R |
0 |
(1.6) |
t a |
|
|
|
(вытекает из свойств 5 и 2) |
|
|
|
или равенству |
|
|
|
lim r |
R |
0 |
|
t a |
|
|
|
Положив r R w , получаем, что равенство (1.5) имеет место
тогда и только тогда, когда r |
R w , где w - вектор, беско- |
нечно малый при t a . |
|
|
|
r |
R |
r |
|
|
R |
Рис.4. |
|
9

Если совместить начало векторов r и R (рис.4), то из ра-
венства (6) для случая R 0 видно, что при t a вектор r и по длине и по направлению неограниченно приближается к
вектору R .
1.4. Свойства непрерывности вектор-функции.
Вектор-функция (1.1) непрерывна, если непрерывны ее
проекции x |
x t , y |
y t , z |
z t . |
В этом случае |
|
|
||||
lim r x |
lim |
x t |
i |
lim y t j |
lim |
z t |
k |
|||
t |
t0 |
t |
t0 |
|
|
t |
t0 |
t t0 |
|
|
x t0 i |
y t0 j |
z t0 k |
|
r t0 |
|
|
|
|||
Т.е. |
|
|
|
|
|
|
|
|
|
|
|
lim r t |
r t0 . |
|
|
|
|
(1.7) |
|||
|
t |
t0 |
|
|
|
|
|
|
|
|
(предел непрерывной вектор-функции при t |
t0 |
равен ее зна- |
||||||||
чению в предельной точке).
Запишем условие непрерывности в другой форме. Дадим переменной t приращение t . Тогда функции x, y, z получат
приращения |
x, |
y, |
z , |
а вектору r |
будет соответствовать |
|
приращение |
r : |
|
|
|
|
|
r |
r t |
t |
r t |
|
|
|
x |
x i |
|
y |
y j z |
z k |
xi y j zk |
xi |
y j |
|
zk, |
|
|
|
т.е. |
|
|
|
|
|
|
|
r |
|
xi |
y j |
zk . |
(1.8) |
10
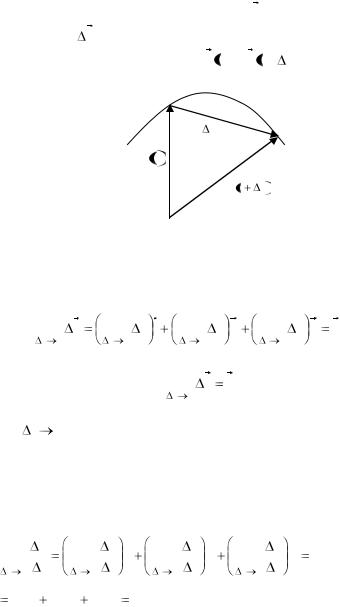
Если считать, что начало вектора r все время совпадает с точкой 0, то r будет вектором, который соединяет точки годографа, отвечающие векторам r t  и r t
и r t  t
t  (рис 5).
(рис 5).
r
r t
|
t |
r t |
О
Рис.5.
Для непрерывной вектор-функции мы при этом получаем
lim |
r |
lim |
x i |
lim |
|
y j |
lim |
z k 0 или |
t |
0 |
t |
0 |
t |
0 |
|
t |
0 |
|
|
|
lim |
r |
0 , |
|
|
|
|
|
|
t |
0 |
|
|
|
|
т.е. приращение непрерывной вектор-функции стремится к 0, если t 0 .
1.5. Свойства дифференцируемой вектор-функции.
Для дифференцируемой вектор-функции существует пре-
дел (см.1.8)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
x |
|
|
y |
|
z |
||||
lim |
|
|
|
lim |
|
|
|
i |
|
lim |
|
j |
lim |
|
k |
|||
t |
|
t |
t |
t |
||||||||||||||
t 0 |
|
|
|
t |
0 |
|
|
|
|
|
t 0 |
|
|
t 0 |
|
(см .II) (1.9) |
||
|
|
|
|
|
dy |
dz |
|
|
|
|
|
|
||||||
|
dx |
|
|
dr |
|
|
|
|
|
|||||||||
|
|
|
i |
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dt |
|
|
dt |
dt |
|
|
|
dt |
|
|
|
|
|
||||
11
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Заметим, |
что вектор |
|
r |
|
всегда направлен вдоль секущей |
|||||||||||||||||||||
|
|
|
t |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
PP , годографа в сторону, отвечающую возрастанию. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
d r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d r |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
Р1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|||
|
|
|
|
|
|
|
d r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
t |
0 |
|
|
|
|
|
||||
|
|
|
|
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
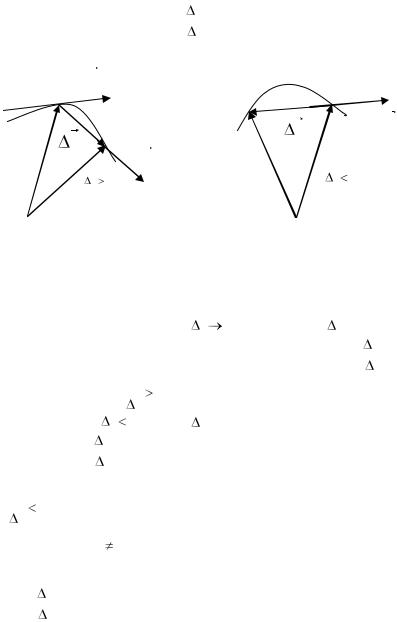
Рис. 6. |
|
|
|
|
|
|
|
|||||
|
|
Действительно, |
если |
|
t |
|
0 , то вектор |
|
направлен в |
|||||||||||||||||||
|
|
|
|
r |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сторону возрастания |
|
t (рис.6а), но тогда и вектор |
|
r |
|
направ- |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||
лен туда же (т.к. |
1 |
|
0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
В случае |
t |
0 вектор |
|
|
направлен в сторону убывания t |
|||||||||||||||||||||
|
|
|
r |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис.6б), но |
|
|
|
|
r |
будет направлен в сторону возрастания t (те- |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dy |
|
|
dz |
|
|
|
|
|
|
|
|
|||
|
|
Пусть |
dr |
0 |
, т.е. |
|
, |
|
, |
не обращаются в 0 одновре- |
||||||||||||||||||
|
|
dt |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
dt |
|
|
|
|
|
|
|
||||||||
менно. Наличие предела (1.9) в этом случае означает, что век-
|
|
|
|
|
|
тор |
r |
по длине и направлению неограниченно приближается |
|||
t |
|||||
|
|
|
|
||
|
|
|
|
||
к вектору |
dr |
. Следовательно, угол между направлением се- |
|||
dt |
|||||
|
|
|
|
||
12
