Учебное пособие 2001

уравнения индикатрисы, заданной уравнением (6.21 ?), то ее значение и решает вопрос о типе данной точки.

Если в данной точки δ>0, то точка эллиптическая, если δ<0, то точка гиперболическая, если δ=0, то точка параболическая. Заметим, что знак δ совпадает со знаком полной кривизны, так как

а дискриминант первой дифференциальной формы в знаменателе всегда положителен.

Таким образом, точка будет эллиптической, гиперболической или параболической, если полная кривизна положительна, отрицательна или равна нулю, соответственно.

Вообще говоря, кроме этих трех возможностей существует еще и четвертая. Может случиться, что в данной точке все коэффициенты D, D', D'' обращаются в нуль одновременно. В таком случае все нормальные сечения имеют кривизны, равную нулю, и понятие индикатрисы Дюпена теряет смысл.

Такие точки называют точками уплощения. Поэтому будем называть точку параболической только в том случае, если δ=0, но при этом среди коэффициентов второй формы Гаусса, соответствующей данной точки, есть отличные от нуля. Полная кривизна в точке уплощения, очевидно, равна нулю.

6.7.2 Строение поверхности вблизи эллиптической точки.

Если индикатриса Дюпена принадлежит эллиптическому типу, то в нормальной системе координат ее уравнение имеет вид

(...)

причем

163

Таким образом, радиусы главных кривизн имеют одинаковый знак. Так как выбор направления нормального вектора зависит от нее, то его всегда можно направить так, чтобы R1 и R2 были положительными.

показывает, что в рассматриваемой точке нормальная кривизна для всех направлений положительна, то есть все нормальные сечения вогнуты. Отсюда следует, что все точки поверхности, достаточно близкие к эллиптической точке, расположены по одну сторону от касательной плоскости в этой точке

(рис. 52).

и данная точка -эллиптическая.

При надлежащем выборе ориентации все сечения в эллиптической точке вогнуты. Поэтому в правой части уравнения индикатрисы следует взять +1 и ее уравнение имеет вид

x2 y 2 1,

1 2

где ρ1 и ρ2 – положительные числа. Таким образом, в эллиптической точке индикатриса будет действительным эллипсом. Если в некоторой точке поверхности индикатриса имеет форму окружности, то эта точка называется омбилической. Так как это возможно только при условии R1=R2, то из формулы Эйлера

164

следует, что все нормальные радиусы кривизны равны между собой.

В общей системе координат омбилическая точка характеризуется пропорциональностью соответствующих коэффициентов обеих квадратичных форм.

D=λE; D'=λF; D''=λG,

т.к. только при этом условии нормальная кривизна, выражаемая отношением обеих форм, не будет зависеть от направления.

Примером омбилической точки может служить всякая точка сферической поверхности.

6.7.3. Строение поверхности вблизи гиперболической точки.

Если точка гиперболическая, то в нормальной системе координат дискриминант ее индикатрисы отрицателен

откуда следует, что главные нормальные кривизны имеют противоположные знаки. Выбрав направление нормального вектора, можно положить

R1=P1>0, R2= –P2<0

и записать формулу Эйлера в виде

где P1>0 и P2>0. Нормальная кривизна в этом случае может принимать положительные и отрицательные значения. Выясним, для каких направлений сечений имеет место та и другая возможность. Из неравенства

165

Обратно, для того, чтобы нормальная кривизна была отрицательной, необходимо и достаточно, чтобы выполнялось условие

Проведем в касательной плоскости через точку касания две прямые с угловыми коэффициентами

которые являются асимптотами индикатрисы Дюпена (рис 53а) Эти прямые разделят касательную плоскость на четыре четверти. Направление прямой, проходящей через точку O из I четверти в III четверть будут вогнуты, а нормальные сечения по направлению прямых, проходящих внутри вертикальных углов II, IV – выпуклы.

Отсюда видно, что обходя по поверхности точку O по достаточно малому замкнутому контуру, мы должны будем два раза перейти из верхней части пространства в его нижнюю часть и два раза совершить обратныѐ переход, если считать, что пространство разделено на эти части касательной плоскостью в данной точке.

Учитывая распределение выпуклых и вогнутых нормальных сечений, можно заключить, что вблизи гиперболической точки имеет седлообразное строение (рис. 53б).

166

Для направления с положительной нормальной кривизной уравнение индикатрисы Дюпена имеет вид

x2 y 2 1

12

адля сечений с отрицательной нормальной кривизной

x2 y 2 1

1 2

Таким образом, индикатриса в гиперболической точке имеет вид двух сопряженных гипербол. Эти гиперболы имеют общие асимптоты, причем действительная ось одной совпадает с мнимой осью другой и наоборот (рис. 53в).

6.7.4. Строение поверхности вблизи параболической точки.

Параболическая точка поверхности характеризуется равенством

δ=DD''–D'2=0,

которое равносильно условию

правление вектора нормали поверхности так, чтобы

167

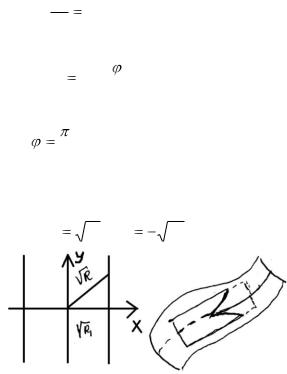
R1=P1>0.

В таком случае уравнение индикатрисы в нормальной системе координат примет вид

x 2 1, (6.25)

P1

а формула Эйлера сведется к соотношению

Отсюда следует, что нормальная кривизна обращается в нуль

Это становится особенно ясным, если учесть форму индикатрисы. Уравнение (6.25) показывает, что она распадается на пару параллельных прямых (рис. 54а)

(рис. 54a) (рис. 54б)

Радиус-вектор любой точки этих прямых имеет конечное значение. Прямая же, совпадающая с осью OY, параллельна обеим прямым, поэтому соответствующая ее направлению нормальная кривизна равна 0. Направление оси OY является одновременно и главным и асимптотическим направлением индикатрисы.

Чтобы выяснить строение поверхности вблизи параболической точки, заметим, что все нормальные сечения можно считать вогнутыми, за исключением сечения, касающегося асимптотического направления индикатрисы. Кривизна последнего в рассматривиемой точке равна нулю, так что она является точ-

168

кой спрямления.

В простейшем случае это будет точка перегиба и тогда поверхность имеет вблизи данной точки “полуседлообразное” строение (рис. 54б).

Отметим существенное отличие между гиперболическими и эллиптическими точками с одной стороны, и параболическими точками – с другой.

Первые два типа точек характеризуются неравенствами δ<0 и δ>0, последние – равенством δ=0.

Это равенство можно рассматривать как соотношение между криволинейными координатами точек, и оно определяет, вообще говоря, некоторую линию, состоящую из параболических точек. Неравенство же определяет не линию, а целые области эллиптических и гиперболических точек.

Если на поверхности есть и та, и другая область, то при условии непрерывности функций, определяющих уравнение плоскости и их производных, эти области разделяются линией δ=0, состоящей из параболических точек.

6.8. Линия пересечения поверхности с ее касательной плоскостью.

Пусть поверхность задана уравнением

Z=f(x,y)

и расположена так, что плоскость XOY касается ее в начале координат. В таком случае линия, определяемая в этой плоскости уравнением

f(x,y)=0,

будет линией пересечения поверхности с этой плоскостью. Координатные векторы

в точке O должны располагаться в плоскости XOY, поэтому

169

Отсюда следует, что начало координат будет особой точкой линии

f(x,y)=0.

Точка касания поверхности и плоскости есть особая точка линии их пересечения. Если поверхность задана явным уравнением, то ее вторая квадратичная форма имеет вид

а в точке O просто равна

Поэтому не трудно установить строение кривой пересечения касательной плоскости и поверхности в точке касания по знаку

1. Если точка эллиптическая, то она изолирована.

6.9. Точки поверхностей II порядка.

В качестве примера приложения классификации точек поверхности рассмотрим различные типы поверхностей II порядка. Всякое плоское сечение поверхности II порядка есть кривая II порядка. Кривизна такой кривой может обратиться в нуль в какой-либо точке в том и только том случае, если эта кривая распадается на пару прямых.

Таким образом, кривизна нормального сечения поверхности второго порядка равна нулю в том и только том случае, если его плоскость содержит прямолинейную образующую этой поверхности.

Если учесть, что в эллиптических точках нормальная кривизна не обращается в нуль, в параболических точках она обращается в нуль для сечения одного направления, а для гиперболических точек для сечений двух направлений, то получим сле-

170

дующие выводы.

1.Эллипсоид, двуполостный гиперболоид и эллиптический параболоид не имеют прямолинейных образующих и, следовательно, состоят из эллиптических точек.

2.Через каждую точку однополостного гиперболоида и гиперболического параболоида проходят две прямолинейные образующие, следовательно, они состоят из гиперболических точек.

3.Через каждую точку цилиндров и конусов II порядка проходит одна прямолинейная образующая, поэтому они состоят из параболических точек.

4.Если поверхность II порядка распадется на пару плоскостей, то она состоит из точек уплощения. (Всякая точка плоскости есть точка уплощения, поскольку все нормальные сечения плоскости – прямые.)

6.10.Сферическое отображение. Гауссова кривизна.

Рассмотрим точку M поверхности и сферу единичного радиуса с центром в начале координат. Ориентируем нормаль поверхности в точке M. Через точку O проведем луч, параллельный этой нормали до точки пересечения его с поверхностью сферы. Получим на сфере некоторую точку M0 (рис. 55а).

ности при ее сферическом отображении. С помощью сферического отображения можно установить соответствие между любой областью точек на данной поверхности и областью точек на сфере единого радиуса.

171

Чтобы получить это соответствие, зададим параметрическое уравнение поверхности

Рассматривая его как радиус-вектор точки на сфере единичного радиуса, мы получим сферическое отображение поверхности, считая соответствующими точки, определенные радиуса-

ми-векторами r и m , взятые при одинаковых значениях криволинейных координат.

С помощью сферического отображения можно определить “кривизну” поверхности по аналогии с ее определением для плоских кривых. Для этих кривых мы можем рассматривать круговое отображение, ставя в соответствие каждой их точке, точку пересечения круга единичного радиуса с радиусом, параллельным ориентированной нормали кривой в данной ее точке (рис. 55б).

Для плоской линии угол между касательными равен иглу между нормалями, а последний равен дуге кругового отображения. Поэтому кривизну плоской кривой можно определить как предел отношения длины дуги кругового отображения к соответствующей длине дуги кривой, когда эта дуга стягивается в данной точке.

Аналогичное определение кривизны поверхностей позволяет выяснить смысл гауссовой кривизны. Переход от кривой к поверхности учтем, заменив дуги площадями, а круговое отображение сферическим.

Будем называть гауссовой (или полной) кривизной поверхности в данной точке предел отношения площади сферического отображения площади сферического отображения области, окружающей данную точку, к площади самой области, предполагая, что область стягивается к данной точке.

Обозначив площади указанных областей Σ0 и Σ через S0 и S соответственно, получим для гауссовой кривизны в точке M

172