
Учебное пособие 2001
.pdf
Поэтому для нее существует обратная функция t t(S ) , кото-
рая также является непрерывной и возрастающей. Для каждой не особой точки для нее существует конечная производная
|
dt |
1 |
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
x2 |
y2 |
|||
|
|
|
|
dt |
|
|
|
|
|
|
|
(по теореме о дифференцировании обратной функции) |
|||||||||||
Так как координаты |
x и |
|
y переменной точки P кривой |
||||||||
являются непрерывными функциями от t , а t , как только что показано, есть непрерывная функция от S , то x и y также
оказываются непрерывными функциями от S :
x x(S), y |
y(S) |
(2.16) |
Таким образом, для кривой |
|
получены новые параметриче- |
AB |
ские уравнения, где параметром служит переменная дуга S . В ряде случаев этот «естественный» параметр S оказывается более удобным, чем произвольный параметр t .
Для функций (2.16) по правилу дифференцирования сложной функции получаем в каждой не особой точке кривой.
dx |
|
dx dt |
|
|
|
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
dt dS |
|
|
x2 |
y |
2 |
|
|
||
dy |
|
dy dt |
|
|
|
y |
(2.17) |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dS |
|
dt dS |
|
|
x2 |
y2 |
|||||
Сказанное о переменной дуге в роли параметра целиком распространяется и на случай пространственной кривой.
2.3.3. Единичный вектор касательной
Пусть пространственная кривая С спрямляема. Если принять за параметр переменную дугу S, отсчитываемую от какойнибудь точки кривой, то уравнение кривой получает вид
23

|
|
x |
x S , y y S , z |
z S |
(2.18) |
|
или в векторной форме (рис.12) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
r S |
xi |
yj |
zk |
|
|
|
|
|
|
|
|
|
|
P(x,y,z)
S
|
|
r |
r S |
O
Рис. 12.
Пусть функции (2.18) дифференцируемы. Известно (2.15), что для любого параметра t
dS |
|
dx |
2 |
dy |
2 |
dz 2 |
|
dt |
|
dS |
|
dS |
|
dS |
|
Положим здесь t=S. Получим
dS |
|
dx |
2 |
dy |
2 |
dz |
2 |
|
|
|
|
|
|
|
(2.19) |
dS |
|
dS |
|
dS |
|
dS |
|
|
|
|
|
Отсюда следует, что кривая лишена особых точек и. следовательно, в каждой точке имеет касательную.
Рассмотрим на кривой произвольную точку P(x,y,z), отвечающую значению S переменной дуги, и обозначим черезS единичный вектор касательной к кривой в этой точке, соответствующий возрастанию S (рис.12). Тогда
24

|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||
dr |
|
dr |
|
или |
dr |
|
dx |
|
dy |
|
dz |
|
|
dS |
|
dS |
|
|
dS |
|
dS |
|
dS |
|
dS |
|
|
|
|
|
|
|
|
|
|
и в силу равенства (2.19)
|
|
|
dr |
(2.20) |
|
dS |
||
|
Таким образом производная вектора r S по длине дуги S
кривой есть единичный вектор касательной к кривой. Формулу (2.20) можно переписать в виде
|
dx |
|
dy |
|
dz |
|
|
|
i |
|
j |
|
k |
|
dS |
dS |
dS |
|||
|
|
|
|
из векторной алгебры известно, что проекции единичного вектора на координатные оси совпадают с его направляющими косинусами. Поэтому
dx |
cos |
, |
dy |
cos , |
dz |
cos |
|
|
|
|
|||||
dS |
dS |
dS |
|||||
|
|
|
|
к этим соотношениям можно придти, положив t=S в формулах
(2.7).
стр.12.Пример1: какая линия является годографом векторфункции
|
|
|
|
r (t) |
a cost * i |
asint * j |
ct * k |
Решение: Запишем параметрические уравнения этой линии. x a cost,
y a sin t, z ct.
25

Этоуравнение винтовой линии.
Пример2: Найти |
|
|
|
2 |
|
|
|
|||
r (t) , если |
r (t) |
cos ti |
sintj |
|||||||
|
|
|
|
|
по формуле ( |
) : |
|
|
||
Решение: Находим r (t) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
, затем |
r |
(t) |
2 cost( |
sint)i costj |
sin 2ti |
costj |
|||||
|
(t) |
|
|
|
|
|
|
|
|
|
r |
2 cos2ti |
sintj . |
|
|
|
|
|
|
||
Ответ: |
|
|
|
|
|
|
|
|
|
|
r (t) |
2 cos2ti |
sintj . |
|
|
|
|
||||
Пример 3: кривую заданную уравнением 2у = 3х -1, где х ≥ 0. задать параметрически, используя в качестве параметра длину дуги S.
|
3x 1 |
|
x(t) t, |
|||
Решение: Имеем y |
Положим: |
|
3t 1 , t ≥ 0. |
|||
2 |
|
y(t) |
||||
|
|
|
2 |
|
||
|
|
|
|
|
|
|
Получили параметрические уравнения данной кривой, следовательно, векторно-параметрические уравнения имеют вид:
|
|
3t 1 |
|
, t ≥ 0. |
|
r (t) |
ti |
|
|
j |
|
2 |
|
||||
|
|
|
|
|
|
пользуясь равенством ( |
) получим |
|
|
||
|
|
|
|
9 |
dt |
13 |
|
13 |
. |
|
S(t) |
x 2 y 2 dt |
1 |
dt |
|||||||
4 |
2 |
2 |
||||||||
0 |
|
|
0 |
|
0 |
|
||||
|
|
|
|
|
|
|
||||
Следовательно, представление кривой с помощью натурального параметра имеет вид:
2 |
|
|
|
|
2 |
|
|
3 |
|
|
1 |
|
|||
|
|
|
s |
(s) и r (s) r ( (s)) |
|
|
|
si |
|
|
|
s |
|
j . |
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
13 |
|
13 |
13 |
|||||||||||
26

2.5 Ориентировочные линии
Введем понятие ориентировочной линии, прежде всего для плоской кривой. Рассмотрим отдельно параметрическое и непараметрическое представление линии.
2.5.1 Параметрическое представление.
График скалярной функции y = f(x) дает важную информацию относительно этой функции, однако не всю информацию о ней: двум разным векторным функциям может отвечать один и тот же годограф.
Это связанно с тем, что точка может двигаться по одной и той же траектории, но разными способами.
В качестве примера рассмотрим две вектор-функции:
|
|
|
и |
|
|
|
r |
(i |
j )t |
r |
(i |
j )t3 (0 ≤ t ≤ 1). |
Каждая из них определяет отрезок прямой, соединяющий точку O(0,0) с точкой А(1,1). Обе функции описывают движения от точки О к точкt А, но эти движения различны.
Пример2: две функции
|
|
|
(0 ≤ t ≤ 2π) и |
|
r |
costi |
sintj |
||
|
|
|
|
(0 ≤ t ≤ 2π) |
r |
cos2ti |
sin 2tj |
||
описываю движение точки по единичной окружности, начинающееся и заканчивающееся в точке (1,0). Оба движения совершаются против часовой стрелки, но в первом случае окружность пробегается один раз, во втором – дважды.
Пример3: Функция
|
|
|
|
r |
costi |
sintj |
(0 ≤ t ≤ 2π) |
Тоже описывает движение по единичной окружности, но ни этот раз – в направлении вращения часовой стрелки.
27

Данные примеры подсказывают следующее определение: Две непрерывные вектор-функции
|
|
a ≤ t ≤ b и |
r |
r (t) |
|
|
|
α ≤ τ ≤ β |
r |
r ( ) |
Определяют одну и ту же ориентировочную линию (или ориентировочную кривую), если существует такая возрастающая непрерывная функция.
t |
( ) |
α ≤ τ ≤ β |
|
(2.21) |
|
такая, что |
|
|
|
|
|
( ) a , ( ) b и |
|
|
α ≤ τ ≤ β |
||
r ( (t)) r ( ) |
|||||
При этом говорят, что функция |
|
получается из |
|
||
r (t) |
r ( ) изме- |
||||
нением параметра τ: t = υ(τ).
Под ориентированной линией С понимают годограф не-
прерывный вектор–функции r (t) , определенной на некотором
отрезке [а, в] вместе со всеми векторными функциями, получающимися из нее изменениями параметра.
Замечание: при измерении параметра можно пользоваться лишь возрастающими функциями.
Если
t 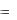 ( ) α ≤ ξ ≤ β
( ) α ≤ ξ ≤ β
есть некоторая убывающая функция, для которой ( ) b , ( ) a , то ориентировочная линия, определяемая функцией
|
|
α ≤ ξ ≤ β |
r |
r ( ( )) |
28

называется противоположно ориентированной (или просто противоположной) по отношению к линии, определяемой функцией
|
|
r |
r (t) , а ≤ t ≤ в |
2.5.2. Непараметрическое представление.
Каждая непрерывная скалярная функция, заданная на некотором интервале, определяет ориентировочную линию. Непараметрическое представление ориентированной линии – это представление ее в виде графика y = f(x). Такое представление всегда может быть преобразовано в параметрическое. Достаточно записать
x(t) t, y(t) f (t) , или |
|
|
|
r (t) |
ti |
f (t) j |
Параметрическое представление иногда может быть преобразовано в непараметрическое.
Пример: какое множество точек, параметрически представляяется функцией.
|
a(1 t2 ) |
2bt |
, - ∞ < t< +∞, |
|
r |
|
i |
|
|
1 t2 |
1 t2 |
|||
где а > 0, b>0- некоторые числа.
Решение: Координаты вектор - функции равны
|
1 |
t2 |
|
|
2t |
|
x(t) a |
|
|
, |
y(t) b |
|
. |
1 |
t2 |
1 t2 |
||||
разделив первое равенство на а, второе – на b, получим
x(t) 1 |
t2 |
a |
|
|
y(t) |
|
2t |
||
|
|
|
|
|
|
|
|
|
|
a |
1 |
t2 |
|
|
b |
1 t2 |
|||
|
|
|
|||||||
29

Возводим обе части полученных равенств в квадрат и складываем почленно:
_ |
x(t) 2 |
|
y(t) 2 |
|
1 2t2 |
|
t4 |
|
4t2 |
|
(1 t2 )2 |
1. |
|||
a2 |
|
b2 |
|
|
(1 t |
2 )2 |
|
(1 t2 )2 |
|
(1 t2 )2 |
|||||
|
|
|
|
|
|
|
|||||||||
Таким образом, |
|
x(t) 2 |
|
y(t) 2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
1. |
|
|
|
||||
|
|
a2 |
|
b2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получили уравнение эллипса.
2.5.3 Формулы в полярных координатах.
Направляющие косинусы плоской кривой получаются из об-
щих формул ( |
), если положить в них z |
= 0: |
|
|
|||||||||||||
cos |
|
x |
|
|
|
|
|
y 2 |
|
|
|
||||||
|
|
|
|
|
|
, cos |
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x 2 |
y 2 |
|
|
x 2 y 2 |
|
|
|
||||||||
Учитывая, |
что |
|
|
, |
|
|
и |
||||||||||
|
2 |
2 |
|||||||||||||||
cos |
cos |
|
|
|
|
sin |
, получим |
|
|
|
|||||||
2 |
|
|
|
|
|
||||||||||||
координаты единого вектора касательной в виде:
cos |
|
x |
|
sin |
|
y 2 |
|
|
. |
(2.22) |
|
|
|
|
|
|
|
||||
|
|
x 2 y 2 |
|
|
|
x 2 |
y 2 |
|
||
Пусть кривая задана в полярных координатах r = r(υ)
Найдем единичный вектор касательной к этой кривой. Для этого, пользуясь формулами перехода от полярных координат
кдекартовым, получим:
xr( )cos , y r( )sin ,
30

Эти формулы можно рассматривать как параметрические уравнения кривой, где параметром служит полярный угол υ.
Т.о.,
dx |
r ( )cos |
r( )sin , |
dy |
r ( )sin |
r( )cos |
|
|
|
|||||
d |
d |
|||||
|
|
|
|
Возводя обе части равенств в квадрат и складывая почленно, получаем:
|
dx |
2 |
|
dy |
2 |
|
|
r 2 ( ) cos2 ( |
|
)sin2 ( |
) |
2r ( |
)r( |
) cos sin |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
d |
|
|
d |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r 2 ( |
)sin2 |
|
|
r2 ( ) cos2 |
|
2r ( )sin |
cos |
r 2 ( |
) r2( |
) |
|||||||||||||||||
Т.е. |
dx 2 |
|
|
dy |
r2 |
|
dr |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d |
|
|
d |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подставляя в формулы (2.22), имеем |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
cos |
|
|
r cos |
|
r sin |
, sin |
|
r sin |
r cos |
, |
(2.23) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
r2 |
|
r 2 |
|
|
|
|
|
|
|
|
r2 |
r 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Угловой коэффициент касательной равен |
|
|
|
|
|||||||||||||||||||||||
|
|
|
tg |
|
dy |
|
r ( |
)sin |
|
r( |
)cos |
|
|
|
(2.24) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
dx |
|
r ( |
)cos |
r( |
)sin |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пусть Р – какая-либо точка кривой. Найдем угол ψ между прямой ОР и касательной к кривой, проходящей через точку Р (рис. 13). Т.к. ψ = α - υ, а угловой коэффициент прямой ОР равен tgυ, то имеем с учетом (2.24)
31

|
Y |
|
|
|
τ |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|||||
|
|
|
|
|
|
ψ |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
α |
|||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
X |
|||
|
Рис.13 |
|
|
|
|
|
|
|
|
|
Рис.14 |
|||||||||
|
|
|
|
|
|
|
|
|
|
r sin |
r cos |
sin |
||||||||
|
|
|
|
|
tg |
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
tg( |
) |
|
|
|
|
r cos |
r sin |
cos |
|
||||||||||
1 tg |
tg |
1 |
|
r sin |
r cos |
|
|
|
sin |
|
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
r cos |
r sin |
|
|
cos |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
После приведения к общему знаменателю (в числителе и знаменателе) и упрощения
tg |
r |
или ctg |
r |
_ |
(2.25) |
|
|
||||
|
r |
r |
|
|
|
Пример: Найти единичный вектор τ(ψ) и tgψ для кривой, заданной уравнением r = υ (0 < υ < ∞) (спираль Архимеда)
Решение: По формулам (2.23) находим проекции единичного вектора.
cos |
|
|
cos |
|
|
|
sin |
|
|
sin |
|
|
|
sin |
|
|
cos |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
cos |
|
|
|
sin |
|
sin |
|
|
|
cos |
|
|
|
||||||
|
( |
) |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
j |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
