Учебное пособие 2001

ских сечения с общей касательной в той точке. Причем одно из них нормальное, а плоскость второго наклонена к плоскости первого под некоторым углом. Для удобства предположим, что направление нормального вектора поверхности выбрано так, что это нормальное сечение вогнуто. В таком случае радиус нормальной кривизны равен радиусу кривизны нормального сечения. Формула (6.7) принимает вид

n cos

Построив центры кривизны для нормального и наклонного сечения, мы получаем из данного соотношения теорему Менье.

Теорема. Центр кривизны наклонного сечения поверхности совпадает с проекцией на его плоскость центра кривизны нормального сечения имеющего ту же касательную, что и данное наклонное сечение (рис.46,а)

144

Если строить центры кривизны различных наклонных сечений касающихся между собой в данной точке поверхности, то любой из них будет служить вершиной прямого угла, опирающегося на радиус кривизны нормального сечения, имеющего данную касательную. Вследствие этого, все центры кривизны будут располагаться на окружности, диаметр которой равен радиусу нормальной кривизны, соответствующей данному направлению (рис.46,б)

Учитывая, что кривизна любой кривой на поверхности равна кривизне плоского сечения, можно сформулировать следующий результат.

Центры кривизны всех кривых поверхности, проходящих через данную точку и имеющих в ней касательную, расположены на окружности, которая лежит в общей нормальной плоскости этих кривых и имеет своим диаметром отрезок между точкой поверхности и центром кривизны нормального сечения.

В качестве следствия из приведенных соотношений отметим, что из всех кривых поверхностей, проходящих через данную точку и имеющих в ней общую касательную, наименьшую кривизну имеют те, соприкасающаяся плоскость которых нормальна поверхности в данной точке. Кривизна других кри-

вых тем больше, чем больше угол (в пределах от 0 до 2 ) меж-

ду соприкасающейся плоскостью этой кривой и плоскостью нормального сечения.

Теорему Менье можно сформулировать иначе, непосредственно исходя из формулы (6.8).

Теорема. Радиус кривизны любой кривой на поверхности в заданной точке равен произведению радиуса кривизны соответствующего нормального сечения в этой точке на косинус угла между нормалью поверхности и главной нормалью к кривой.

145

То есть радиус кривизны любой кривой на поверхности равен проекции радиуса кривизны соответствующего нормаль-

6.4. Индикатриса Дюпена.

Выше было показано, что изучение кривизны всех линий на поверхности сводится к рассмотрению плоских сечений, а кривизна произвольного сечения очень просто связана с кривизной нормального сечения. Таким образом, весь вопрос о кривизне линий на поверхности свелся к рассмотрению кривизны нормального сечения.

Через данную точку поверхности можно провести бесчисленное множество нормальных сечений. Выясним, как изменяется нормальная кривизна поверхности при переходе от одного такого сечения к другому. Для этого воспользуемся графическим метом, предложенным Дюпеном.

Возьмем на поверхности некоторую точку М и будем откладывать от нее на касательной к каждому нормальному се-

146

визны этого нормального сечения. Знак (±) выбираем так, чтобы под корнем оказалась положительная величина. Геометрическое место концов N построенных отрезков есть некоторая плоская кривая, расположенная в касательной плоскости поверхности. Эта кривая называется индикатрисой Дюпена, соответствующей данной точке поверхности.

Найдем ее уравнение. Предположим, что поверхность параметризирована и установим в касательной плоскости сиспримем примем коор-

точки.

говоря, косоразличные индикат- N тогда ее ра-

Рис.48

С другой стороны, по построению тот же радиус-вектор равен

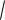n , где - единичный вектор касательной дан-

147

Знак плюс в правой части отвечает случаю вогнутого, а минус - выпуклого нормального сечения. Уравнение (6.9) есть уравнение второй степени относительно ( , ), так как коэф-

фициенты D, D', D'' не зависят от направления сечения, то есть для данной точки постоянны. Кроме того, данной уравнение не содержит первых степеней координат и . Таким об-

разом, индикатриса Дюпена есть центральная кривая второго порядка, центр которой совпадает с рассматриваемой точкой поверхности. Кривая эта дает геометрически наглядное представление об изменении величины радиуса кривизны при вращении нормального сечения вокруг нормали к поверхности.

6.4.1. Формула Эйлера. Главные радиусы кривизны.

Уравнение (6.9) индикатрисы Дюпена можно упростить обычными методами аналитической геометрии, то есть за счет выбора системы координат. Однако в рассматриваемом случае система декартовых координат в касательной плоскости связана с системой криволинейных координат на поверхности. Вы-

148

ка, то в ее уравнении отсутствует член с произведением координат. Значит, в нашем случае для точки О коэффициент

Получим теперь формулу Эйлера, выражающую зависимость между нормальной кривизной любого направления и нормальными кривизнами главных направлений индикатрисы. Обозначим угол между главным направлением и направлением произвольного сечения через υ.

Тогда для координат точки индикатрисы будут иметь место очевидные соотношения

мального сечения. Подставив выражение координат в (6.10), получим

Главными радиусами кривизны нормальных сечений R1 и R2 поверхности в данной точке называются радиусы кривизны, соответствующие главным направлениям индикатрисы Дюпена.

В нашем случае эти направления определяют значе-

ниями υ=0 и υ= 2 , поэтому

150

Это и есть формула Эйлера, которая дает выражение нормальной кривизны, соответствующей любому направлению, через значения главных кривизн и угол между одним их главных направлений индикатрисы Дюпена и данным направлением.

Так как направления осей ОХ и ОУ совпадают направлениями осей симметрии кривой (6.9) и, очевидно, что для этих

направлений радиус-вектор индикатрисы, равный R , имеет максимум и минимум. То же самое будет иметь место и для

самого R и для кривизны R1 . Данный результат сформируем в

виде теоремы.

Теорема 3. в каждой точке поверхности существуют два взаимно перпендикулярные направления в касательной плос-

кости, для которых кривизна 1 достигает максимума и ми-

R

ниям значения кривизны, то кривизна любого нормального сечения, выражается по формуле (6.11), где υ – угол, образованный касательной с тем направлением, которое дает кри-

визну 1 .

R1

6.5. Определение главных радиусов кривизны и главных направлений.

Перепишем основную формулу (6.4) для кривизны нормального сечения в виде

Edu2 2Fdudv Gdv2 RDdu2 2RD'dudv RD''dv2

151

dv

к нормальному сечению. Тогда

R,tDR E t 2 2 D'R F t D''R G 0

Это уравнение определяет радиус кривизны R нормального сечения в зависимости от t: R=R(t). Для главных направлений величина R должна достигать максимума или минимума, следовательно, производная от R по t должна обращаться в нуль. Найдем ее

152