Учебное пособие 2001

Обе площади можно вычислить по формуле (…)

D

применяя ее один раз к данной поверхности, а другой раз к единичной сфере, заданной (6.27). Получим

Здесь Σ – обозначение области изменения криволинейных координат u и v, которая одна и та же для обоих интегралов. Чтобы установить связь между гауссовой кривизной и коэффициентами дифференциальных квадратичных форм, сравним векторные произведения

Оба они направлены соответственно по нормалям к данной поверхности и поверхности сферы. Так как эти нормали в соответствующих точках параллельны, то и векторы коллинеарны

Для вычисления λ умножим обе части этого равенства скаляр-

Заменив скалярные произведения коэффициентами основных квадратичных форм, получим

DD''-D'2 (EG F 2 )

Отсюда

λ=k,

где k – полная кривизна поверхности. Таким образом,

На основании этой формулы площадь сферического отображения

173

Применяя к интегралу теорему о среднем, получим

Значок c указывает, что полная кривизна берется в некоторой внутренней точке области Σ.

Возвращаясь к выражению гауссовой кривизны, получим

Но область Σ стягивается к точке M, следовательно, к той же точке стремится и точка c, откуда

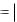GM k M ,

так что гауссова кривизна совпадает с полной кривизной поверхности.

Задачи для самостоятельного решения.

есть однополостный гиперболоид, а координатные линии совпадают с его прямолинейными образующими.

2. Составить параметрическое уравнение кругового цилиндра

Ответ. r ae( ) vk . Координатные линии – прямолиней-

молинейные образующие и их ортогональные траектории. Угол α образующая составляет с плоскостью XOY.

4. Составить уравнение касательной плоскости кругового цилиндра.

Ответ. e( ) a 0.

5. Составить уравнение касательной плоскости кругового ко-

174

6. Найти линейный элемент плоскости в полярных координа-

7. Найти линейный элемент сферы в географических коорди-

10. Найти длину дуги кривой, заданной внутренним уравнением

v=u

на поверхности с линейным элементом dS 2 du2 sh2udv2

Ответ. S shU2 shU1 .

11. Найти угол, под которым кривые v Aem

пересекают прямолинейные образующие кругового конуса.

12. Доказать, что линейный элемент всегда может быть выражен в виде

175

14. Составить параметрическое уравнение тора и найти его линейный элемент.

15. Составить выражение вторых квадратичных форм следующих поверхностей.

в) Гиперболического параболоида. z=mxy.

Сравнивая с выражением линейного элемента сферы, получим

16. Найти главные значения кривизны геликоида.

176

Замечание.

Геликоид есть линейчатая поверхность, образованная главными нормалями винтовой линии (рис. 56). Уравнение геликоида

Геликоид можно рассматривать как винтовую поверхность, описываемую прямой, пересекающей ось вращения под прямым углом.

(рис. 56) Линейный элемент геликоида dS 2 (a 2 t 2 )d 2 dt 2 .

Его можно привести к “изотермическому” виду, положив t=ashu; υ=u.

Тогда

dS 2 a 2 ch 2u(du2 dv2 ) .

17. Найти полную и среднюю кривизну поверхности Z=f(x,y).

18. Найти главные радиусы кривизны в данной точке геликои-

да x=ucosv; y=usinv, z=kv.

19. Найти главные радиусы кривизны поверхности az=xy в произвольной точке

177

21. Найти главные радиусы кривизны поверхности sinZ=shxshy.

янно для всех точек эллипсоида с концентрической ему сферой.

23. Доказать, что соприкасающийся круг винтовой линии есть большой круг сферы, соприкасающийся с прямым круговым цилиндром, на котором начерчена винтовая линия.

24. Вычислить полную кривизну для параболоида

равна 0.

26. Составить выражение для средней и полной кривизны поверхности вращения.

2(1 f 2 ) 3

27.Доказать, что для омбилической точки H2=K.

28.Доказать, что в точке с равным нулю значением средней кривизны асимптотические направления индикатрисы Дюпена взаимно перпендикулярны.

178

29. Найти геометрическое место главных центров кривизны поверхности xy=az для оси OX.

сти кривые. Найти геометрической место их центров кривизны.

Ответ. x2+y2+z2=ax

31.Показать, что линии пересечения эллипсоида с софокусными ему одно- и двуполостными гиперболоидами будут линиями кривизны для эллипсоида.

32.Показать, что геодезическая линия для сферы будет дуга окружности большого круга.

6.11 Асимптотические линии.

Линия, расположенная на поверхности, называется асимптотической, если касательная плоскость поверхности совпадает в каждой ее точке с соприкасающейся плоскостью этой линии.

Если на поверхности расположена прямая линия, то ее тоже следует считать асимптотической, так как любая содержащая ее плоскость может рассматриваться как соприкасающаяся. В обоих случаях нормальная кривизна асимптотической линии равна нулю во всех е точках, так как вектор ее кривизны или перпендикулярен нормали к поверхности, или равен нулю. Таким образом, асимптотическая линия есть линия нулевой нормальной кривизны.

Асимптотическая линия является ребром возврата для семейства плоскостей, касающихся поверхности в ее точках. Поэтому характеристики семейства этих плоскостей совпадают с касательными к самой линии.

Таким образом, направление касательной к асимптотической линии в каждой точке совпадает с асимптотическим направлением индикатрисы Дюпена этой точки. Исходя из ра-

179

венства нулю нормальной кривизны асимптотических линий можно получить их дифференциальное уравнение в виде

отождествляя направления, du и dv с δu, δv.

Чтобы привести это уравнение к нормальному виду

dv f (u, v) du

нужно разрешить его как квадратное относительно dudv . При этом возможны следующие случаи.

1.В области эллиптических точек DD''–D'2>0 и оба корня этого квадратного уравнения будут комплексными. Это значит, что в области эллиптических точек асимптотические линии не существуют.

2.В области гиперболических точек DD''–D'2<0 уравнение (6.28) имеет два действительных различных корня. Оба уравнение получающиеся в результате разрешения квадратного уравне-

ния, определяют два семейства асимптотических линий, которые составляют асимптотическую сеть.

3.В области параболических точек DD''–D'2=0 и оба корня уравнения совпадают и действительны. Из единственного уравнения

равносильного (6.28), определится одно семейство асимптотических линий.

4. В области точек уплощения D=D'=D''=0 уравнение (6.28) удовлетворяется тождественно. Поэтому всякая линия в этой области – асимптотическая.

7. Огибающие семейства кривых и поверхностей. 7.1. Огибающая плоских кривых.

Уравнение

180

F(x,y,a)=0 (7.1)

левая часть которого непрерывная и дифференцируемая функция трех переменных, определяет плоскую кривую при каждом фиксированном значении параметра a. Придавая a различные значения, можно получить бесконечное множество кривых.

Совокупность всех таких кривых образует семейство кривых зависящих от параметра a. Во многих случаях семейство допускает существование кривой, которая в каждой своей точке касается некоторой кривой семейства. Такая линия называется огибающей данного семейства кривых (рис. 57а).

(рис. 57a) (рис. 57б) (рис. 57с)

Точка прикосновения огибающей к кривой семейства называется характеристической точкой кривой семейства.

Пусть семейство, определенное уравнением (7.1), имеет огибающую. По определению, каждая точка огибающей принадлежит некоторой кривой семейства, а это кривая определяется значением параметра a. Поэтому можно считать, что координаты точек огибающих будут функциями параметра a:

x=x(a); y=y(a), (7.2)

и рассматривать эти зависимости как параметрические уравнения огибающей. Так как всякая точка огибающей принадлежит одной из кривых семейства, то подстановка выражений (7.2) в (7.1) приводит к равенству

F={x(a); y(a); a}=0, (7.3)

справедливому при всяком значении a. Дифференцируя по a, получим

Если уравнения кривой семейства имеют вид x=x(t); y=y(t),

181

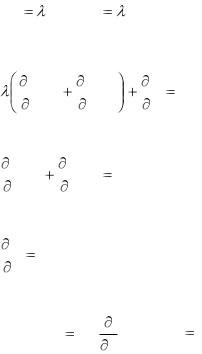
то условием прикосновения этой кривой и огибающей будет пропорциональность координат касательных векторов

в точке прикосновения. Подставим (7.5) в (7.4) и приведем его к виду

Однако координаты вектора касательной кривой семейства должны удовлетворять для всякой ее точки условию

откуда следует, что координаты характеристической точки удовлетворяют равенству

Таким образом, если огибающая неизвестна, то координаты ее точек следует искать, решая совместно уравнения

F(x, y, a) 0 ; a F (x, y, a) 0 . (7.7)

Разрешая эти уравнения, мы определим x и y в зависимости от a и найдем так называемую, дискриминантную кривизну данного семейства.

Из сказанного следует, что огибающая, если она существует, должна входить в состав дискриминантной кривой, которая может иметь несколько ветвей.

Выясним теперь, при каких условиях кривая x=x(a); y=y(a),

полученная при решении системы (7.7), действительно будет огибающей. Для этого подставим найденные выражения в первое из уравнений (7.7), обратив его в тождество

F={x(a); y(a); a}=0.

Дифференцируя и учитывая второе уравнение (7.7), получим

182