
Учебное пособие 2001
.pdf
1. |
x |
6t, y |
|
|
3t 2 , z |
|
|
|
t3 |
в точке t=1. Ответ: |
2 |
|
; |
2 |
|
. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
27 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
x |
cost, y |
sint, z |
cht при t=0. Ответ: |
2 (кривизна). |
||||||||||||||||||||||||||||||||||||||||||
3. |
x2 |
|
y2 |
|
|
|
z2 |
|
1, y2 2x |
z |
|
0 |
|
в точке (1,1,1). |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
6 |
|
|
|
(кривизна). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
x |
et cost, y |
et sint, z |
et |
|
в произвольной точке. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
t 4 |
|
|
y |
|
t3 |
z |
|
|
t 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e t |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
t |
. |
|
4 |
|
3 |
|
|
|
2 |
|
|
||||||||||||||||||||||
|
K |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
3e |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
T |
|
|
|
1 |
|
|
|
|
2t |
|
|
t 2 |
||||||||||||||||||||||||
5. |
x |
acht, y |
asht, x |
et |
в произвольной точке. |
||||||||||||||||||||||||||||||||||||||||||
Ответ: |
|
K |
|
|
|
|
|
|
|
|
1 |
|
|
, |
1 |
|
|
|
|
2ach2t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2ach t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6. |
x2 |
|
y2 |
|
|
|
|
|
z2 |
|
4 |
|
|
|
0, x |
|
y |
|
|
z |
0 в произвольной точке. |
||||||||||||||||||||||||||
Ответ: |
|
K |
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в произвольной точке. |
|||||||||||||||||||||||||||||
r |
costi |
|
|
|
|
|
sintj |
|
shtk |
||||||||||||||||||||||||||||||||||||||
Ответ: |
1 |
|
|
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
T |
|
|
|
|
|
|
|
ch2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
в произвольной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
r |
t 2i |
|
|
2t3 j |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: R |
|
|
|
t(1 |
|
9t 2 )2 |
T=∞/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. y |
x2 |
|
, z |
|
2a |
|
|||
|
|
|
||
Ответ: |
|
K |
1 |
|
|
|
T |
||
|
|
|
|
|
10. y2 |
|
x, x2 |
||
Ответ: |
1 |
|
|
|
|
T |
|
|
|
|
|
|
|
|
x3 в произвольной точке.
6a2
(x aa)2 .
z в произвольной точке.
12y .
64y6 36y 1
113
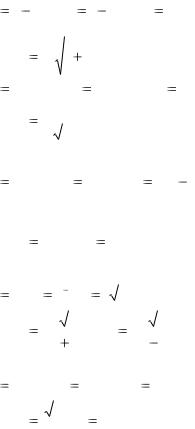
11. x |
t |
sint, y |
1 |
|
|
|
|
|
cost, z |
|
|
4sin |
t |
в произвольной точке. |
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
K |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
sin |
2 t |
. |
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
12. x |
achtcjst, y |
|
|
|
achtsint, z |
at в произвольной точке. |
|||||||||||||||||||||||||||||||||
Ответ: |
K |
|
|
1 |
|
|
|
|
|
|
|
|
|
sht |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
ch2t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
13. x |
a |
cost |
, y |
|
a |
sint |
|
, z |
a(t tht) в произвольной точке. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
cht |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cht |
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: |
K |
|
|
2 |
|
|
|
|
, |
|
1 |
|
|
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
acht T |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
14. x |
et , y |
e t , z |
|
|
|
|
|
|
|
в произвольной точке. |
|||||||||||||||||||||||||||||
|
t t |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
. |
||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(x |
|
|
|
|
|
|
y)2 |
T |
|
|
(x |
|
y)2 |
|||||||||||||||||||||||||
15. x |
et sint, y |
et cost, z |
et |
в произвольной точке. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ: |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|||||||||||||||
K |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3et |
|
T |
|
|
|
|
|
3et |
|
|
|
|
|
|
||||||||||||||||||||||||
5. Дифференциальная геометрия поверхностей 5.1. Теория поверхностей в трехмерном пространстве 5.1.1. Общие замечания
До сих пор мы изучали линии и их метрические инварианты на плоскости и в пространстве ( нормаль, каса-тельная, бинормаль, кривизна, кручение, формулы Френе). Но эти инварианты зависят от способа вложения линии в пространство. В этом смысле они являются инвариантами лишь способа вложения, формы линии, т.е. это понятие внешней геометрии (по отношению к линии). Никаких внутренних метрических инва-
114

риантов на линии не бывает.Однако можно выбрать вдоль линии натуральный параметр (S), в котором длина отрезка кривой между точками измеряется так же, как и на прямой.
Для поверхностей это уже не так. Например, никаким образом нельзя задать координаты на сфере (даже на части сферы) так, чтобы формулы длин кривых в этих координатах были такими же, как формулы длины кривых в декартовых координатах x,y на плоскости.
Но поверхности в трехмерном пространстве – это простейший объект на котором возникает внутренняя геометрия.
Интуитивные представления о поверхности в трехмерном пространстве имеются у каждого человека. Далее будет сделана попытка очень кратко, формально описать эти представления, ограничиваясь сравнительно узким классом поверхностей.
Каковы существуют способы задания поверхностей? Существуют три способа задания поверхностей. До сих пор мы рассматривали в курсе математического анализа два из них.
1.простейший - графиком функции z = f(x, y).
2.более общий – уравнением F(x, y, z) = const
3.параметрический – (по аналогии с кривыми) Определение 1. Говорят, что уравнение F(x, y, z) = const
задает поверхность не особую в |
|
точке P0 (x0 , y0 , z0 ) , |
где |
|||||||||||
F( x0 , y0 , z0 ) = const, если градиент функции F в точке P0 |
от- |
|||||||||||||
личен от нуля: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
F (P0 ) |
|
|
|
F (P0 ) |
|
|
|
|
F (P0 ) |
|
|
|
|
|
i |
|
|
j |
|
k 0 |
|
|||||||
|
|
|
|
|
|
|
||||||||
|
x |
|
y |
|
|
|
|
z |
|
|||||
т.е. все частные производные в точке P0 |
одновременно в нуль |
|||||||||||||
не обращаются |
|
|
|
|
|
|
|
|
|
|
|
|||
5.1.1. Параметрический способ задания поверхностей
Ранее рассматривалось параметрические уравнения кривой в пространстве
x = x(t), y = y(t), z = z(t),
115

так что положение точки на кривой определялось значением одного параметра t, изменяющегося в некотором промежутке.
При определении положения точки на поверхности, заданной явным уравнением z = f(x, y) мы имеем дело уже с двумя параметрами, роль которых здесь играют абсцисса х и ордината у. В общем случае в качестве параметров вводят две произвольные переменные u и v и параметрическое представление
поверхности осуществляется с помощью трех уравнений |
|
x = x(u, v) y = y(u, v) z = z(u, v) |
(5.1) |
Данные функции определены и непрерывна в некоторой области «плоскости параметров» (u, v)
Мы будем, главным образом, рассматривать “простые” поверхности, когда уравнения (5.1) устанавливаю взаимнооднозначное соответствие между точками поверхности и точками плоской области в плоскости (u, v) Стр.61 Параметры u и v называются криволинейными координатами соответствующей точки.
Здесь мы подходим к понятию так называемой внутренней геометрии поверхности, сформированной Гауссом. Суть заключается в том, что каждую поверхность можно рассматривать с двух точек зрения.
Вчастности, рассмотрим плоскость. В стереометрии плоскость рассматривается как частный случай поверхности, и наряду с точками и прямыми являются одним из основных образов пространства. Там изучается ее расположение и отношение
кдругим образам пространства.
Впланиметрии плоскость выступает как бы вне всякой зависимости от вмещающего ее пространства, и сама является областью, в которую вмещены все изучаемые образы.
Сопоставляя эти две точки зрения, можно сказать, что стереометрия изучает внешнюю геометрию плоскости, а планиметрия ее внутреннюю геометрию.
Перейти от рассмотрения отдельных и весьма малочисленных линий элементарной геометрии к рассмотрению кривой вообще позволяет аналитический метод. То же самое справед-
116
ливо и в отношении поверхностей. Поэтому, желая распространить основные понятия планиметрии на случай произвольной поверхности, следует распространить на случай поверхности метод аналитической геометрии.
Но этот метод есть метод координат, позволяющий определить положение точки на плоскости с помощью двух чисел.
Аналогичный способ задания положения точки на поверхности и есть метод “криволинейных координат”, установленный Гауссом.
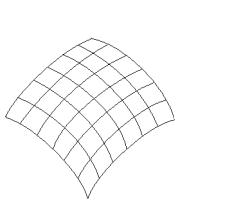
5.2. Криволинейные координаты
Если в уравнениях (5.1) фиксировать значение одного из параметров, положив, напри-
v=v5 v=v4 мер, u=u0, то очевидно получаются уравнения
некоторой кривой
x=x(u0,v), y=y(u0,v), z=z(u0,v),
которая всеми точками лежит на поверхности. Изменяя значение u0, получим целое семейство таких “кривых (u)”. Аналогично, фиксируя
Рис.36.
значение v=v0, получим также кривую на той же поверхности x=x(u,v0), y=y(u0), z=z(u,v 0),
из таких “кривых (v)” также составляется целое семейство
(рис.36).
V=v0
Выясним условия, при которых около не особой точки пверхности P(x0, y0, z0) можно задать локаль-ные регулярные координаты U, V.
117

Пусть поверхность задана уравне-ниием F(x, y,z)=C. По теоре-
ме о неявных функциях, если |
F |
|
≠ 0, |
|
|
||||
Z |
||||
|
|
|
||
|
|
|
то уравнение поверхности можно решить относительно z в окрест- U=u0 ности точки P0 (x0, y0, z0): где z=f(x,y),
где z0=f(x0, y0), причем F(x, y, f (x, y)) ≡ C в некоторой области плоскости XoY, окружающий точку (х0, у0). Отсюда получаем, беря дифференциал от обеих частей^
|
|
F |
|
dx |
F |
dy |
|
F |
dz |
0 , |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
x |
y |
|
|
|
z |
|
|
|
|||||||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
F |
|||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
||||
и |
|
F |
x |
, |
y |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
F |
|
y |
F |
|
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|||
Следовательно, для поверхности F(x, y, z)=С около точки (x0, y0, z0) можно написать параметрическое представление z=f(u,v), x=u, y=v. Т.о., локально, около неособой точки поверхности, всегда можно задавать поверхность параметрически, т.е. можно задавать локальные криволинейные координаты. Если поверхность является простой, то через каждую ее точку проходит по одной координатной линии из каждого семейства.
Предположим теперь, что функции (5.1), задающие поверхность параметрически не только непрерывны, но и имеют непрерывные частные производные первого порядка в некоторой области. Тогда можно определить неособую точку
P0(x0, y0, z0)=P0[(x(u0, v0), y(u0, y0), z(u0,v0)]
следующим образом.
118

Определение 2. Точка Р0 на поверхности называется неособой, если в функциональной матрице
x |
|
y |
|
z |
|||
|
|
|
|
|
|
|
|
u |
|
u |
|
u |
|||
x |
|
y |
|
z |
|||
|
|
|
|
|
|
|
|
v |
|
v |
|
v U U ,V V |
|||
для значений параметров (u0, v0), определяющих точку Р0 поверхности, отличен от нуля хотя бы один определитель второго порядка (т.е. ранг данной матрицы равен 2).
Можно доказать, что если поверхность задана параметрически, и точка Р0-неособая, то около этой точки поверхность можно задать уравнением
F(x, y, z) = 0, где F(x0, y0, z0) = 0 и gradF |
x |
, y |
, z |
0 , |
|
0 |
0 |
|
0 |
т.е. определение 2 и определение 1 эквивалентны. |
|
|||
Вывод состоит в том, что локально, около неособой точки |
||||
Р0(x0, y0, z0) на поверхности, все три способа задания поверхностей (гладкими функциями) эквивалентны.
Рассмотрим параметры поверхностей и координатных линий.
Пример1. Эллипсоид |
x2 |
|
y 2 |
|
z 2 |
1 (рис.37.) |
a2 |
|
b2 |
|
c2 |
||
|
|
|
|
|
|
Z |
|
|
|
На этой поверхности имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) особых точек нет; |
|
|
|
|
|
|
|
б) в целом поверхность |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
нельзя задать графиком |
|
|
|
|
|
|
|||
Рис37 |
|
||||||
|
|
||||||
функции (локально можно); |
|
|
|||||
119

в) в целом поверхность нельзя задать параметрически (так чтобы все точки были неособые)
Z |
|
Пример 2. Однополостный ги- |
|||||||
|
|
перболоид (рис.38). |
|
|
|
|
|||
|
|
Эту поверхность |
|
|
|
|
|
||
|
|
а) в целом нельзя задать в виде |
|||||||
|
|
графика |
|
|
|
|
|
|
|
|
|
б) в целом можно задать пара- |
|||||||
X |
Y |
метрически |
|
|
|
|
|
|
|
|
|
Пример 3. Двуполостный гипер- |
|||||||
|
|
болоид - |
x2 |
- |
y 2 |
+ |
z |
2 |
= 1 |
|
|
a2 |
b 2 |
c2 |
|||||
|
|
|
|
|
|
||||
Рис.38 |
|
(рис.39а) |
|
|
|
|
|
|
|
Z |
Z |
|
|
|
|
|
X |
|
|
. |
X |
|
|
|
||||
|
Y |
|
|
|
|
||
|
|
|
|
Y |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис.39а |
Рис.39б |
Эта поверхность такова, что одну половину можно задать как в виде графика Z=f (x,y), так и параметрически.
120

Пример 4. Конус |
z 2 |
+ |
y2 |
- |
z 2 |
= 0 |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Здесь точка (0,0,0) особая.
5.3. Примеры криволинейных координат
Рассмотрим простейшие примеры координатных сеток, начиная с декартовой координатной сетки плоскости, которая является как бы прообразом всех остальных.
1. Два семейства параллельных прямых, образованных прямыми различных направлений (например, ортогональных междусобой) образуют сеть. Параметризируя эти семейства так, чтобы каждой прямой соответствовало значение расстояния этой прямой от некоторой принятой за начальную, и приписывая этому знак мы и получим обычную (косоугольную) декартовую систему координат. (рис.40а).
(а |
(б |
(в |
|
Рис.40 |
|
2. Рассмотрим сетку, образованную пучком лучей, выходящих из некоторой точки и семейством концентрических окружностей с центром в этой точке. Оба семейства имеют по одной точке пересечения за исключением начала. Это особая точка координатной сетки. Параметризируем семейство прямых, принимая за параметр угол υ между начальной прямой (υ=0) и данной прямой пучка. Каждой окружности семейства сопоставим значение ее радиуса. Полученная таким образом система координат совпадает с полярной (рис.40б).
121

3. Географические” координаты на сфере. Фиксируем «полярную ось” – один из диаметров этой сферы. Рассмотрим лярную ось» - один из диаметров этой сферы. Рассмотрим семейство меридианов – больших кругов, полученных от пересечения поверхности сферы плоскостями, содержащими этот диаметр.
Параметризируем его, приняв за параметр “долготу” (υ), т.е. угол между плоскостью меридиана, принятого за нормальный, и плоскостью данного меридиана. (рис.40в). Второе семейство “параллелей” получим, пересекая поверхность сферы плоскостями, перпендикулярными “полярной оси”. Это семейство будет содержать один большой круг – “экватор”.
За параметр второго семейства принимается “широта” θ – угловая мера дуги меридиана, заключенной между плоскостью экватора и плоскостью данной параллели. Широте приписывается знак в зависимости от того, на каком полушарии (“северном” или “южном”) расположена параллель.
Оба семейства будут правильными на всей поверхности сферы за исключением “полюсов”. (рис40в).
5.4. Векторно-параметрическое уравнение поверхности.
Если на поверхности введены криволинейные координаты, то говорят также, что поверхность параметризирована. В таком случае, всякой паре значений параметров u и vсоответствует определенная точка поверхности.
Поэтому, отвлекаясь от координатных осей, можно охарактеризовать поверхность переменным радиусом – вектором
r u, v , идущем из постоянной точки О в переменную точку М
поверхности. Можно сказать, что переменная r является функцией двух скалярных аргументов и записать это так:
|
|
r |
r u, v |
|
122 |
