Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 2001

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Или в силу независимости скалярного произведения от поряд-

ка множителей

	dA A 0 , т.е.		dA ┴ A , ч.т.д.


	dt		dt

Как мы уже знаем,(		) производная		dr	дает вектор касатель-
Как мы уже знаем,(		) производная		dt	дает вектор касатель-
				dt

ной к кривой (рис.15б). если за параметр принять длину дуги S кривой, отсчитываемую от определенной точки кривой в опре-

деленном направлении,

то производная

дает единичный

вектор касательной

(

), направление которого совпадает с

направлением возрастания параметра S вдоль кривой.

(3.2)

Рассмотрим теперь вектор

. Этот вектор имеет важ-

ds2

ное значение и называется вектором кривизны. Обозначим

(3.3)

При переходе к другой точке Р; соответствующей значению S+∆S, переменной дуги, вектор получает некоторое приращение

∆ =	(S + ∆S) – (S) (рис 16)

В силу доказанной леммы вектор кривизны направлен перпендикулярно касательной, т.е. по нормам. Кроме того, из его определения непосредственно следует, что он направлен в сто-

рону вогнутости кривой, так как в эту сторону направлена разность ∆ при ∆S > 0 (рис.16)._

Определение: кривизной

плоской кривой называется

модуль вектора N

(3.4)

Рис.16 Величина, обратная кривизне, называется радиусом кривизны

1.2. Формулы для кривизны плоской кривой.

1.2.1. Параметрическое задание кривой

Пусть плоская кривая задана уравнениями x = x(S), y = y(S)

или в векторной форме r (s)

yj ,причем функции x(S) и

y (S) дважды дифференцируемы. Тогда

d 2 y

d 2r d 2 x

ds ds2

ds2

и, по определению

(3.5)

ds2

Эта формула неудобна для практического применения, так как обычно кривая задается уравнениями (3.1) с произвольным параметром t или уравнением вида

y = f(x),

(3.6)

т.е. явная зависимость х и у от переменной S не задается. Поэтому в формуле (3.5) следует от производных по S перейти к производным по t.

Пусть х и y одновременно в нуль не обращаются (расматривается неособая точка). Тогда по формуле(….)

Следовательно,

xdt

sdt

ds2

sdt

2 xx

Находим

S :

2 x 2

y 2

Подставив S

и S , после несложных преобразований по-

лучим

d 2 x xy 2

xyy

ds2

y 2 2

Аналогично

d 2 y

xy 2

xyy

ds2

y 2

Поэтому

d 2 x 2

y 2

xy 2

2 x 2

xy 2

y 2 4

ds2

y 2 4

Подставляя эти значения в формулу (3.5), получим

(3.9)

x 2

y 2

Так вычисляется кривизна в случае, когда плоская кривая задается уравнениями вида (3.1).

Для радиуса кривизны плоской кривой в соответствии с определением получаем

	x 2		y 2	3

R				2	(3.10)
		xy	xy

3.2.2. Кривая задана явным уравнением свойства кривизны

Пусть теперь кривая задана уравнением вида (3.6), причем функция f(x) дважды дифференцируема. Такое задание является частным случаем параметрического задания, когда роль параметра выполняет переменная x. Положим

x(t) = t, y(t) = f(t), тогда

x t	1;
x t	0,
y t	f t ,
y t	f "(t)

Потому формулы (3.9) и (3.10) приобретают вид

K (3.11)

	1	y'	2
			2	2


		y'2		3
	1
R	1			2	( 3.12)
		y"

Замечание. В формулах (3.11) и (3.12) часто опускают знак абсолютной величины, и тогда K и R становится величинами со знаком.

Этот знак указывает, в какую сторону обращена выпуклость кривой. Как известно, если y`` 0, то выпуклость кривой в данной точке обращена вниз, если y`` 0, то вверх.

Соответствует ли введенное понятие кривизны наглядным представлениям? В связи с этим рассмотрим свойства кривизны.

1. Кривизна прямой равна нулю.

Доказательство. Пусть x = x0+as, y = y0+bs – прямая, при-

чем параметр t – натуральный, тогда						dx	а		dy	b и

						ds			ds

	dr			d 2 r
		аi	bj;		0 и K= 0, R= .
	ds	аi	bj;	ds2	0 и K= 0, R= .
	ds			ds2
2. Кривизна окружности радиуса R равна							1	.
2. Кривизна окружности радиуса R равна								.
							R

Параметрические уравнения имеют вид

х R cost y R sin t

0 t 2.

x R sin t,

x R cost,

Следовательно, По формуле (3.9) полу- y R cost,

	y	R sin t
чаем
K	R cost R cost	R sin t R sin t			R 2		1
	R cost R cost	R sin t R sin t			R 2		1

		3		3				R
		3		3
	R 2 sin2 t	R 2 cos2 t			R 2
	R 2 sin2 t	R 2 cos2 t	2		R 2	2

Т.о., кривизна окружности во всех точках равна R1 ,

Рассмотрим примеры.

Пример 1. Найти кривизну параболы y = x2. В какой точке кривизна будет наибольшей?

Решение. y` = 2x y`` = 2. По формуле (3.11) получим

	2
K	3 .	Эта величина будет наибольшей при

1 4x2 2

наименьшем знаменателе, т.е. при x = 0: K = 2 Пример 2. Найти радиус кривизны для эллипса

х = aсost, y = bsint в точке, для которой t 3 . x а sin t;

Решение.

x а cost; y b cost;

y	b sin t
		а2 sint	b2сost	3
По формуле (3.10)	R	а2 sint	b2сost	2	.
По формуле (3.10)	R		аb		.
			аb

3.2.3 Кривая задана уравнением в полярных координа-

тах.

Пусть кривая задана уравнением r = r ( ) в полярных координатах. Пользуясь формулами перехода от полярных координат к декартовым, запишем

x = r( )соs ,

y = r( )sin

Эти формулы можно рассматривать как параметрические уравнения линии, где параметрам служит полярный угол . Найдем производные.

	x` = r`cos		- r sin ,	y` = r`cos + r sin ,
х	r	cos	2r sin	r cos ,
y	r	sin	2r cos	r sin

Вычислим выражения, входящие в формулу (3.9).

направлению совпадающий с В силу (3.4)

ничный вектор кривизны

Пусть дана кривая и на ней точки P, и пусть в точке P кри-

визна кривой отлична от 0: K 0. введем в рассмотрение еди-

3.2.4. Окружность кривизны (соприкасающаяся окружность), центр кривизны.

N Kn

, т.е. вектор длины единицы, по

После несложных преобразований получим

r" r 2r'2 r 2

x 2

y 2

r 2 r 2

Подставляя в формулы (3.9) и (3.10), получим для кривиз-

ны и радиуса кривизны

r"r 2r'2

r 2

(3.13)

r 2

r'2

r 2

r'2

(3.14)

r"r

2r'2

r 2

где r’

d 2 r

Очевидно, что введенный таким образом вектор n есть ни что иное, как единичный вектор нормали к кривой в точке P

(см.п. 2.54).

	.
	.
	C			.P2




		n


.			.
.			P

Рис. 17

Отложим на направлении n , т.е. на направлении нормали кривой в

сторону вогнутости, отрезок PC длины R (рис. 17). Из полученной точки радиусом R опишем окружность. Эта окружность называется окружностью кривизны или соприкасающейся ок-

ружностью.

Центр этой окружности, т.е. т. C называется центром кривизны для

кривой в точке P.

Очевидно, что круг кривизны касается кривой в точке P. Существует бесконечное множество окружностей, касаю-

щихся кривой в точке P. Окружность кривизны среди них играет особую роль в силу следующего утверждения.

Окружность кривизны представляет собой предельное положение окружности, проходящей через точку P и две другие точки P1 и P2 кривой, когда последние стремятся к P. (рис. 17)

Можно показать, что окружность кривизны касается кривой – в некотором смысле – особенно тесным образом. По построению окружность кривизны в точке P имеет ту же кривизну, что и рассматриваемая кривая в этой точке. Поэтому в приложениях участок кривой вблизи точки P часто заменяют другой окружности кривизны.

Найдем координаты центра кривизны C ( ). Радиусвектор точки C обозначим (рис. 18). По построению центра

		1
кривизны вектор c	Rn		n
		K

Тогда из векторного треуголь-

ника				1		(3,16)
	r	Rn	r		n
				K

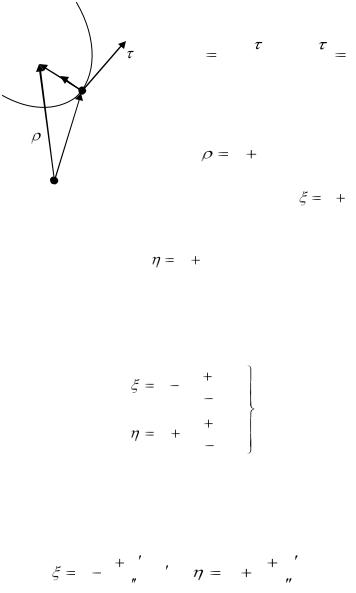
В силу формул (3.3) и (3.4)

1 d

d 2 r

C(ξ,η

, но

K ds

ds2

P(x, y)

Поэтому

d 2 r

K 2

ds2

Отсюда

d 2 x

K 2

ds2

Рис.18.

d 2 y

K 2

ds2

Воспользовавшись формулами (3.7) и (3.8) для

d 2 x

d 2 y

ds2

и формулой (3.9)

для K, получим

x 2

(3.17)

x 2

Получены формулы, для координат центра кривизны кривой, заданной параметрическими уравнениями.Для случай кривой, заданной явным уравнением вида y = f(x) можно получить

	1	y 2				1 y	2
x			y	,	y			(3.18)
x			y	,	y			(3.18)
		y				y

3.3. Эволюта и эвольвенты.

Если точка (x,y) перемещается вдоль кривой, то соответствующий ей центр кривизны C( ) также перемещается, описывая некоторую кривую, называемую эволютой данной кривой.

Иными словами, эволютой плоскости кривойназывается геометрическое место центров ее кривизны.

Исходная кривая по отношению к своей эволюте называется эвольвентой.

Формулы (3.17) и (3.18), выражающие координаты и центра кривизны C через параметр t (или x), можно рассматривать как параметрические уравнения эволюты.

Иногда если это бывает нужным, из этих уравнений удается исключить параметр и получить для эволюты неявное уравнение F( , ) = 0.

Рассмотрим примеры.

Пример 1 Найти эволюту параболы y = ax2

Решение. y` = 2ax y`` = 2a. По формуле (3.18)

x	1 4а2 х2	2ах х 1	1 4а2 х2		4а2 х3
	2а			n

1 4а2

х2

ах2

1 4а2

х2

1 6а2 х2

2а

4а

6а2 х2

Т.е.

2а

Это – параметрические уравнения эволюты. Роль параметра играет x, который можно исключить. Действительно из уравнений получаем:

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.72 Mб3Учебное пособие 1999.pdf
#
30.04.2022157.23 Кб7Учебное пособие 2.pdf
#
30.04.2022214.94 Кб1Учебное пособие 20.pdf
#
30.04.2022326.11 Кб2Учебное пособие 200.pdf
#
30.04.20223.82 Mб2Учебное пособие 2000.pdf
#
30.04.20223.83 Mб8Учебное пособие 2001.pdf
#
30.04.20223.83 Mб4Учебное пособие 2002.pdf
#
30.04.20223.84 Mб3Учебное пособие 2003.pdf
#
30.04.20223.86 Mб10Учебное пособие 2004.pdf
#
30.04.20223.87 Mб5Учебное пособие 2005.pdf
#
30.04.20223.89 Mб4Учебное пособие 2006.pdf