Учебное пособие 2001

dt dt2

Эта формула позволяет вычислить кручение кривой в произвольной точке, если кривая задана параметрическими уравнениями с произвольным параметром t.

Пример 2. Вычислить кручение винтовой линии r t a costi a sin t j htk

Решение: Записываем производные

93

Находим смешанное произведение числителя в формуле (4.13)

Знаменатель этой формулы был вычислен при решении при-

мера1 в п. 4.3.3.1

Как и кривизна, кручение винтовой линии оказывается постоянным.

4.3.4 Формулы Френе

Формулы, выражающие производные векторов ,b, n по натуральному аргументу S, называются формулами Френе:

Первая формула непосредственно следует из ( ),вторая из (4.6). Последняя из них получается следующим образом. За-

94

пишем равенство (следует непосредственно из рассмотрения рис. 28)

n b

Дифференцируя обе части равенства по S, получим

Часто формулы Френе записывают в координатной форме. Координатами единичного вектора являются направляющие косинусы, т. е. косинусы углов, образованных вектором с положительными направлениями координатных осей.

В рассматриваемом случае это будет направляющие косинусы осей подвижного репера относительно неподвижных координатных осей, как указано в таблице. Здесь введены обозначения

cos ,i , cos , j 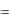, cos , k ,

В результате формулы Френе в координатной форме можно записать следующим образом.

95

Нормалью к кривой в точке Р называют всякую прямую, проходящую через эту точку перпендикулярно к касательной. Таких нормалей бесконечное множество; они заполняют собой плоскость, которая называется нормальной (пл.II. рис. 31).

r=r(s)

Рис.31

(I –соприкасающаяся, II –нормальная,III –спрямляющая плоскости)

Т. о., вектор n является одной из нормалей к кривой в

ной плоскости. Следовательно, плоскость, определяемая векторами n и b - нормальная.

Плоскость I, которую определяют векторами и n , называются соприкасающейся плоскостью, для данной кривой в точке Р.

Наконец плоскость, определяемая векторами и n называется стпрямляющей плоскостью.

Рассмотренные три плоскости образуют так называемый естественный трѐхгранник, связанный с переменной точкой Р кривой. Рѐбрами этого трѐхгранника служат касательная к кривой, главная нормаль и бинормаль.

97

В связи с понятием «соприкасающаяся плоскость» сделаем следующие замечания.

Рассмотрим прямую, касательную к кривой в точке Р. Всякая плоскость, проходящая через эту прямую, будет касаться кривой в точке Р (рис. 32а). Очевидно, что таких плоскостей имеется бесконечное множество.

а) б) в)

Рис. 32.

Среди них находится и соприкасающаяся плоскость. На особую роль которой указывают следующие утверждения (без доказательства).

1. Соприкасающаяся плоскость в точке Р кривой представляет собой предельное положение плоскости F, проходящей через касательную в точке Р и через точку Р’ кривой при условии, что P' P (рис. 32б).

2. Соприкасающаяся плоскость в точке Р кривой представляет собой предельное положение плоскости F, проходящей через точку Р и через две другие точки P’ и P’’ кривой при условии что последние стремятся к Р (рис. 32в).

Можно показать, что соприкасающаяся плоскость касается кривой в некотором смысле особенно тесным образом.

Наконец двугранный угол между соприкасающимися плоскостями, соответствующими двум точкам кривой, равен углу между бинормалями. Тогда по аналогии с формулой ( ) можно записать

98

где - угол поворота бинормали (угол смежности второго рода) на участке кривой MN.

В заключении запишем уравнения прямых и плоскостей, связанных с пространственной кривой.

1. Уравнение касательной к пространственной кривой в произвольной точке Р(x, y, z) в канонической форме имеют вид

T ddtr .

Из условия перпендикулярности прямой и плоскости получается уравнение нормальной плоскости

Tx ( X x) Ty (Y y) Tz (Z z) 0

Заменяя в данных уравнениях Tx ,Ty ,Tz на Bx , By , Bz , где

N B T (вектор главной нормали) получим уравнения бинормали и главной нормали или соответственно, соприкасающийся плоскости и спрямляющей плоскости.

Замечание. Если кривая задана как пересечение двух плоскостей,

F(x, y, z)=0, G(x, y, z)=0,

d r dx, dy, dzи d 2 r d 2 x, d 2 y, d 2 z . При этом одну из пере-

менных x, y, z можно считать независимой и полагать еѐ второй дифференциал равным нулю.

4.5. Винтовые линии. Свойства.

99

Но x'( ) и y'( ) равны, соответственно, косинусу и

синусу угла, образованного касательной к кривой (l) c осью

Ox.

Определим косинус угла, образованного касательной к линии (l) с осью Оz.

Получим первое свойство винтовой линии: касательные к винтовой линии образуют постоянный угол с некоторым выбранным направлением.

Запишем теперь третью из формул Френе (4.14): ddS R1 .

главная нормаль винтовой линии перпендикулярна оси Oz, т. е. к образующей цилиндра. Но она, с другой стороны, перпендикулярна и касательной к винтовой линии.

Как нетрудно видеть (рис. 33), образующая цилиндра и касательная к винтовой линии определяют касательную плоскость к цилиндру во взятой точке на винтовой линии. Из сказанного следует, что главная нормаль винтовой линии стр51перпендикулярна к этой касательной плоскости. Получено второе свойство винтовой линии:

Главная нормаль к винтовой линии во всех точках совпадает с нормалью к цилиндру, на котором эта винтовая линия начерчена.

Рассмотрим теперь косинусы , 1, 2, - углов, образованных осью OZ с направлениями , n, b подвижного репера

101

на постоянная.

Третье свойство винтовой линии: вдоль винтовой линии отношение радиуса кривизны к радиусу кручения есть величина постоянная.

Взаключении выясним еще одно важное свойство винтовых линий. Если взять на цилиндре две точки, то кратчайшее расстояние между двумя точками на цилиндре дает винтовая линия, проходящая через две эти точки. В этом отношении винтовые линии на цилиндре совершенно аналогичны прямым линиям на плоскости.

Указанное свойство выражают, говоря, что винтовые линии есть геодезические линии цилиндра.

Вообще геодезическими линиями на заданной поверхности называют линии, дающие кратчайшее расстояние между двумя точками поверхности.

Если развернуть цилиндр на плоскость XoZ, поворачивая его вокруг образующей, проходящей через точку А, то в силу того, что отношение дуги AN к отрезку N′M сохраняет постоянное значение 1/k, винтовая линия на плоскости окажется прямой линией (рис 33).

При указанной развертке цилиндра на плоскость длины сохраняются, и упомянутое свойство винтовой линии – давать кратчайшее направление на цилиндре – становится очевидным.

Данное свойство находится в непосредственной связи со вторым свойством винтовой линии, т. е. с тем фактом, что главные нормали винтовой линии совпадают с нормалями к цилиндру.

Вгеометрии вообще доказывается, что главные нормали к геодезической линии на любой поверхности совпадают с нормалями к этой поверхности,

102