
Учебное пособие 2001
.pdf
бы t |
|
du , |
то совершенно также получили бы для главных |
|
|||||||||||||||||||||
1 |
|
dv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направлений равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
D'R |
F du |
|
D'' R |
G dv 0 |
|
|
|
|
|
(6.14) |
|
||||||||||||
|
Перенеся в равенствах (6.13) и (6.14) члены с dv напра- |
|
|||||||||||||||||||||||
во и почленно деля одно равенство на другое, получим |
|
|
|||||||||||||||||||||||
|
|
DR |
E |
|
|
D'R |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
D'R |
F |
|
D''R |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DR E D''R |
|
|
|
D'R F |
2 |
|
|
|
|
|
|
||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
DD''R2 |
DGR |
ED''R |
EG |
D'2R2 |
2FD'R |
F 2 |
0 |
||||||||||||||||
|
|
DD'' |
D'2 |
R2 |
|
2FD' |
|
ED'' |
|
GD R |
EG |
F 2 |
0 |
||||||||||||
(6.15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Это квадратное уравнение и дает нам R1 и |
R2 . Раздели |
|
||||||||||||||||||||||
его на R2, получим квадратное уравнение для определения |
|
||||||||||||||||||||||||
кривизны главных сечений, Тл есть |
1 |
и |
1 |
: |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
R2 |
|
|
|
|
|
|
|
|
|
EG |
F 2 |
|
1 |
|
2FD' |
ED'' |
GD |
|
1 |
|
DD'' |
D'2 |
0 |
||||||||||
|
|
|
|
R |
|
R |
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.16) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Выражение |
K |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(6.17) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
R1R2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Называется Гауссовой кривизной поверхности в заданной точке, а выражение
153

Н |
1 |
1 |
1 |
(6.18) |
|
2 |
R1 |
|
R2 |
||
|
|
|
|||
называется средней кривизной. Из квадратного уравнения (6.16) получаем непосредственно (по теореме Виета) выражение Гауссовой и средней кривизны через коэффициенты первой и второй формы Гаусса:
|
K |
DD'' |
D'2 |
; Н |
ED' 2FD' GD |
(6.19) |
|||
|
|
EG |
F 2 |
2 EG |
F 2 |
||||
переменим (6.13) и (6.14) в виде |
|
|
|||||||
Ddu D'dv R |
Edu |
Fdv; D'du |
D''dv R |
Fdu Gdv |
|||||
разделив почленно одно равенство на другое, исключим R. |
|||||||||
|
Ddu |
D'dv |
|
Edu |
Fdv |
|
|
||
|
D'du D''dv |
Fdu |
Gdv |
|
|
||||
или |
|
|
|
|
|
|
|
|
|
FDdu2 GDdudv FD'dudv GD'dv2 
EDdu2 FD'dudv ED''dudv FD''dv2
FD ED' du2  GD ED'' dudv
GD ED'' dudv  GD' FD'' dv2 0
GD' FD'' dv2 0
(6.20)
Деля последнее равенство на du2, получим квадратное уравнение относительно dudv . Его два корня дадут нам величи-
ны, характеризующие главные направления в каждой точке поверхности:
du |
du |
|
dv |
1 u,v ; dv |
2 u,v ; |
(6.21)
154
6.6. Линии кривизны. Теорема Дюпена.
Линией кривизны на поверхности называется такая линия на поверхности, у которой в каждой ее точке касательная направлена по главному направлению.
Так как в каждой точке поверхности имеются два главных направления, то мы будем иметь два семейства линий кривизны на поверхности эти семейства будут взаимно ортогональны. Таким образом, совокупность всех линий кривизны дает некоторую ортогональную сетку на поверхности. Уравнение (6.20) или эквивалентные ему уравнения (6.21) являются дифференциальными уравнениями линий кривизны. Интеграция их, можно выразить V через U. Подставляя это выражение в уравнение поверхности, получим уравнения линий кривизны.
Пусть на поверхности дана некоторая координатная сетка. Выясним условия, при которых эта сетка есть сетка линий кривизны. Прежде всего, раз эта сетка должна быть сеткой линий кривизны, то она должна быть ортогональной сеткой, то есть должно быть F=0.
Кроме того, раз координатные линии u=c1 ,v=c2 есть линии кривизны, то уравнение (6.20) должно удовлетворяться при подстановке вместо u и v постоянной. Принимая во внимание уже полученный результат F=0, будем иметь ED’=0,GD’=0. но мы видим, что разность EG-F2>0, следовательно величины E и G не могут быть равны нулю. Поэтому из двух последних формул вытекает, что М=0.
Таким образом, необходимым условием того, чтобы координатная сетка была сеткой линий кривизны, является условие
F=D’=0
Наоборот, если это условие выполнено, то дифференциальное уравнение линий кривизны (6.20) имеет решение u=c1 ,v=c2, то есть координатные линии есть линии кривизны. Получена следующая теорема:
155

Необходимое и достаточное условие того, чтобы координатная сетка была сеткой линий кривизны, заключается в том, что в двух дифференциальных формах Гаусса средние коэффициенты на всей поверхности равны нулю, то есть F=D’=0.
Пусть в пространстве имеются три семейства взаимно перпендикулярных поверхностей
x, y, z q1, x, y, z q2, x, y, z q3,
Они образуют сетку ортогональных криволинейных ко-
ординат в пространстве. Радиус-вектор r из начала координат в переменную точку пространства М характеризуется криволинейными координатами q1 , q2 , q3 этой точки
r r q1 , q2 , q3 
Геометрическое место точек, для которых одна их координат сохраняет постоянное значение, есть некоторая поверхность, называемая координатой. Действительно, если, на-
пример, q3 =const, то радиус-вектор r r q1 , q2 , с зависит от
зависит от
двух параметров, определяя точку координатной поверхности. Координатные поверхности различных семейств пересекаются попарно по координатным линиям. Вдоль каждой из этих линий изменяется только одна координата, две другие ос-
таются постоянными (рис.50)
156

Рис. 50.
Частные производные rq1 ;rq 2 ;rq3 дают векторы, на-
правленные по касательной к координатным линиям. Условие ортогональности координат можно записать в векторной форме:
|
|
|
0; rq' |
3 rq'1 0; rq'1 rq' |
2 0 |
|
r |
r |
q3 |
(6.22) |
|||
q 2 |
|
|
|
|
|
Дифференцируем первое равенство по q1, второе q2 и третье по q3:
'' |
|
|
|
|
|
|
|
|
|
'' |
|
|
|
|
|
r |
|
|
r |
|
r |
|
|
|
|
r |
0 |
||||
q q |
2 |
|
q |
3 |
|
|
q q |
3 |
q |
2 |
|||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||
'' |
|
|
|
|
'' |
|
|
|
0 |
||||||
r |
q |
|
r |
|
r |
|
|
q |
r |
||||||
q |
3 |
|
q |
|
|
|
q |
2 |
q |
3 |
|||||
2 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|||
'' |
|
|
|
|
'' |
|
|
|
|
|
0 |
||||
r |
|
|
r |
|
r |
|
|
q |
|
|
r |
||||
q q |
3 |
|
q |
2 |
q |
2 |
3 |
q |
|
||||||
1 |
|
|
|
|
|
|
|
1 |
|
||||||
отсюда непосредственно получаем
157
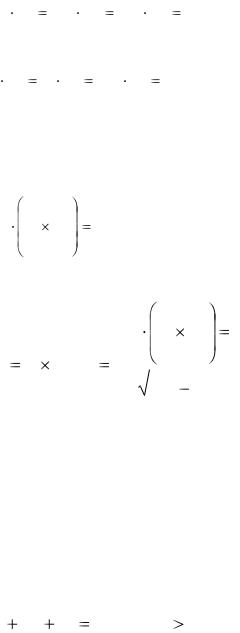
'' |
|
' |
'' |
|
|
' |
'' |
' |
0 |
|||||
r |
|
r |
|
r |
|
q |
|
r |
|
r |
q |
r |
|
|
q q |
2 |
q |
3 |
q |
2 |
3 |
q |
2 |
q |
q |
2 |
|
||
1 |
|
|
|
|
|
3 1 |
|
|
||||||
Сопоставим равенства
' |
' |
|
' |
' |
'' |
|
' |
|
|
|
|
|
|
||||
r |
|
0 |
|
|
|
|
|
||||||||||
r |
r |
|
|
|
r |
|
r |
|
r |
|
|
|
|
|
|
||
q |
q |
3 |
q |
2 |
q |
3 |
q q |
2 |
q |
3 |
|
|
|
|
|
||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||
Из |
них |
следует, что |
|
векторы |
' |
' |
'' |
перпендику- |
|||||||||
|
r |
; r |
|
; r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
q |
2 |
q q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
||
лярны одному и тому же вектору rq'3 . Следовательно, они компленарны. Значит, их смешанное произведение равно 0.
'' |
|
|
' |
|
' |
|
|
0 |
|
|
|
|
|
(6.23) |
||
r |
|
r |
|
r |
|
|
|
|
|
|
|
|
||||
q q |
2 |
q |
q |
2 |
|
|
|
|
|
|
|
|
|
|
||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
В соответствии с (5.9) и (6.25) |
|
имеем |
||||||||||||||
|
|
|
|
|
|
|
|
|
'' |
|
' |
r |
' |
0 |
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|||
|
|
|
|
|
|
|
|
|
q q |
2 |
q |
q |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|||
|
|
' |
' |
|
' |
|
|
|
|
|
|
|
|
|||
F |
r |
|
r |
|
|
; D |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
q |
q |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
EG |
F 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
и равенства (6.22) и (6.23) показывают, что в данном случае F=D’=0, то есть координатные линии q1 и q2 есть линии кривизны на поверхности q3 = const. Это приводит к следующей теореме Дюпена.
Если в пространстве имеются три семейства взаимно ортогональных поверхностей, то любые две поверхности из разных семейств пересекаются по линии, которая является линией кривизны для обеих этих поверхностей.
Пример1. Уравнение сжатого эллипсоида вращения
x2 |
|
y2 |
|
z2 |
1 |
( a |
2 |
c |
2 |
) |
a2 |
|
a2 |
|
c2 |
|
|
||||
|
|
|
|
|
|
|
|
158

может быть записано в параметрической форме в следующем виде
x a cosu sin v; y a sin u sin v; z c cosv
координатные линии u=c1, очевидно, является линиями пересечения эллипсоида с плоскостями y=xtgc1. Это - меридианы. Координатные линии u=c2 - параллели, получаемые от пересечения эллипсоида z=ccosc2, перпендикулярными оси вращения.
Применяя (5.9), (5.11), (6.5) и учитывая, что x,y,z явля-
ется составляющими вектора r , получим
E a2 sin 2 v; F |
0;G |
a2 cos2 v c2 sin 2 v |
|
||||||
D |
|
acsin2 v |
|
; D' |
0; D'' |
|
ac |
|
|
|
|
|
|
|
|
|
|||
a2 cos2 v |
c2 sinv |
a2 cos2 v c2 sinv |
|
||||||
|
|
|
|
|
|
|
|||
равенства F=0 и D’ = 0 можно было предвидеть в силу того, что меридианы и параллели являются линиями кривизны эллипсоида вращения. Остальные коэффициенты зависят только от параметра v, характеризующего положение точки на меридиане.
Главные направления очевидно совпадают с касатель-
ными к меридиану и параллели. Выражение DD'' D'2  в
в
данном случае положительно на всей поверхности, то есть все точки поверхности – эллиптические.
Не вычисляя в отдельности главные радиусы кривизны приведем лишь выражение для гауссовой кривизны
К |
1 |
DD'' |
D'2 |
c2 |
|
R R2 |
EG |
F 2 |
a2 cos2 v c2 sin2 v 2 |
||
|
|||||
|
1 |
|
|
|
Пример2. Уравнение конуса второго порядка
159

x2 |
|
y2 |
|
z2 |
0 |
a2 |
|
a2 |
|
c2 |
|
|
|
|
перепишем в явной форме
z c |
x2 |
|
y2 |
a2 |
|
b2 |
Дифференцируя, получим коэффициенты (6.6’).
p |
z c2 x |
;q |
z c2 y |
;r |
2 z |
|
c4 y2 |
|
||||||
x |
2 |
z |
|
2 |
z |
x |
2 |
|
2 2 |
z |
3 |
|||
|
a |
|
y b |
|
|
|
a b |
|
||||||
S |
c4 xy |
|
;t |
c4 x2 |
|
||
2 2 |
z |
3 |
2 2 |
z |
3 |
||
|
a b |
|
|
a b |
|
||
Пользуясь (6.7’) модно определить все коэффициенты форм Гаусса. Заметим, что в данном случае rt-S2 =0, то есть все точки поверхности являются параболическими. Один из главных радиусов кривизны бесконечен.
Соответствующее главное направление совпадает, очевидно, с прямолинейной образующей конуса.
Пример3. рассмотрим гиперболические параболоид
z |
x2 |
|
y2 |
|
|
|
|
||
2a2 |
|
2b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
В данном случае z |
1 |
;S 0;t |
1 |
. |
|||||
a2 |
|
||||||||
|
|
|
|
|
|
|
b2 |
||
Так что rt-S2 <0 , и, следовательно, каждая точка поверхности является гиперболической точкой. Две прямолинейные образующие поверхности дают в данном случае направление асимптот индикатрисы Дюпена, которая состоит из двух сопряженных гипербол. Аналогичное обстоятельство имеет место и для однополостного гиперболоида.
160
6.6 Радиусы кривизны поверхности вращения.
Плоскость всякого меридиана поверхности вращения есть ее
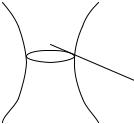
плоскость симметрии. Отсюда следует, что индикатриса Дюпена, построенная для какой-либо точки поверхности вращения, должна быть симметрична относительно плоскости меридиана, проходящей через эту точку. Но ось симметрии кривой второго порядка совпадает с одной из ее главных осей. Таким образом, одно из главных направлений поверхности вращения, в данной ее точке, совпадает с направлением меридиана, а другое, перпендикулярное первому, есть направление касательной к параллели. Установив это, выясним, чему будут равны радиусы кривизны главных направлений. Так как меридиан является одним из главных сечений, то один из радиусов главной кривизны совпадает с радиусом кривизны меридиана.
|
|
|
|
|
Центр кривизны нормального се- |
|
|
|
|
|
|
|
|
|
|
|
чения Cn, касающегося паралле- |
|
|
С2 |
|
ли, должен, по теореме Менье, |
|
|
|
|
|
|
проектироваться в центр кривиз- |
|
|
|
|
|
|
С |
|
|
С1 |
ны самой параллели C, а послед- |
|
|
|
ний, очевидно, лежит на оси |
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
вращения в плоскости параллели. |
|
|
|
|
|
Отсюда следует, что Cn лежит на |
|
|
|
|
|
|
(рис. 51) |
|
оси вращения |
|||
Таким образом, второй радиус кривизны равен отрезку нормали между точкой поверхности и осью вращения.
Знаки главных кривизн определяются положением центра кривизны меридиана. Если он расположен по ту же сторону от точки меридиана, что и ось вращения, то есть, если меридиан обращен вогнутостью к оси вращения, то обе главных кривизны имеют одинаковые знаки. В противном случае их знаки различны.
В заключение рассмотрим кривизну линий на сфере. Всякое нормальное сечение сферы радиуса a есть круг того же радиуса. Поэтому радиус нормальной кривизны во всякой точке
161

сферы и для всякого направления равен радиусу сферы. Чтобы получить индикатрису, нужно откладывать от данной точки отрезок равный a. Поэтому индикатриса будет окружностью. Но всякий диаметр окружности есть ее главный диаметр, поэтому оба радиуса кривизны сферы следует считать равными радиусу сферы. Отсюда следует, что и полная и средняя кривизна сферы будет постоянны.
K a12 ; H 1a .
Полная кривизна сферы будет положительной, так как центры кривизны всех нормальных сечений совпадает с центром сферы, то есть расположены по одну сторону от касательной плоскости.
6.7 Классификация точек поверхности. 6.7.1 Общие замечания.
Выше было показано, что каждой точке поверхности соответствует индикатриса Дюпена, то есть некоторая кривая второго порядка. Как и всякая кривая второго порядка, она может принадлежать к эллиптическому, гиперболическому или параболическому типу.
Ниже мы увидим, что эти возможности действительно могут иметь место для различных поверхностей или даже различных точек одной и той же поверхности.
В связи с этим точки поверхностей распределяются на три класса и называются эллиптическими, гиперболическими и параболическими, в зависимости от того к какому из этих трех типов принадлежит индикатриса Дюпена, соответствующая этим точкам.
Чтобы определить какому, классу принадлежит данная точка поверхности, достаточно вычислить коэффициенты второй квадратичной формы и составить дискриминант этой формы
DD''-D'2 |
(6.24) |
Так как величина δ является дискриминантом старших членов
162
