Учебное пособие 2001

Полученная формула показывает, что на данной поверхности угол между двумя кривыми зависит лишь от отношения дифференциалов криволинейных ординат, взятых вдоль кривых в точке пересечения.

Из формулы (5.15) легко получить выражение косинуса для координатного угла, т.е угла между линиями координатной сетки. Действительно для этих линий можно считать

В частности для того, чтобы координатные линии пересекались под прямым углом (ортогональная сеть), необходимо и достаточно, чтобы F = 0 и линейный элемент имел вид

Такой вид имеют линейные элементы плоскости в прямоугольных и полярных координатах и сферы географических координат, т.к. во всех этих случаях условие ортогональности выполнено.

Пример. Найти угол, под которым кривые V Aem

5.7.2. Площадь поверхности

133

Выведем выражение для элемента площади поверхности через коэффициенты выражения (5.10). Определение длины дуги кривой линии сводится к вычислению суммы длин прямолинейных отрезков с последующим переходом к пределу.

Аналогичным образом и определение пощади частей криволинейной поверхности сводится к измерению площадей плоских фигур.

Разобьѐм заданную на поверхности область на элементарные части сеткой координатных линий (рис.44) Пусть (u,v) – координаты основной вершины А. Малой площадки ABCD. Еѐ сто-

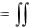
S EG F 2 dudv

D

Таким образом, для вычисления площади некоторой области D поверхности достаточно знание линейного элемента поверхности.

134

9.Найти линейный элемент конуса.

Ответ: dS2 dv2 v2 cos2 du2

6.Кривизна линий на поверхности. 6.1.Нормальная кривизна.

Кривизны линий, расположенных на поверхности, связаны рядом замечательных соотношений. Для того чтобы получить эти соотношения, следует изучить расположение сопровождающего трѐхгранника кривой по отношению к поверхности. При этом касательный вектор кривой всегда расположен в касательной плоскости поверхности, а векторы главной нормали и бинормали наклонены под некоторыми углами к этой плоскости.

Рассмотрим вектор кривизны кривой, расположенной на поверхности:

Проекция вектора кривизны линии на нормаль поверхности в точке, через которую проходит эта кривая, называется нормальной кривизной данной кривой.

При этом нормаль считается ориентированной с помощью за-

ранее выбранного единичного вектора нормали n . Нормальная кривизна обозначается через R1 . Обратная ей величина R на-

зывается радиусом нормальной кривизны.

Так как нормаль считается ориентированной, то проекция r на неѐ может быть положительной или отрицательной. Поэтому радиус нормальной кривизны выражается числом со знаком. Этим он существенно отличается от положительного радиуса кривизны кривой, рассматриваемой независимо от поверхности.

Т.о., по определению, нормальная кривизна

136

6.2. Вторая дифференциальная квадратная формула Гаусса.

Рассмотрим какую - нибудь линию (L) на поверхности и путь– еѐ единичный вектором касательной. Для вычисления нормальной кривизны будем дифференцировать вектор

Пользуясь правилами дифференцирования сложной функции, получим

Скалярные произведения единичного вектора нормами n и вторых частных производных радиуса – вектора точка поверхности являются функциями точки. Введем для них обозначения

137

Выражение, стоящее в правой части данного равенства называется второй дифференциальной формой Гаусса,

Так как (6.3) можно переписать в виде

то нормальная кривизна равна отношению второй и первой дифференциальных квадратных форм

При этом обе квадратные формы определены для отношения дифференциалов криволинейных координат, соответствующих направлению кривой, проходящей через точку поверхности, для которой выполнены коэффициенты обеих форм.

Запишем выражение коэффициентов второй квадратичной формы в развернутом виде. Так как

В заключении отметим другие выражения для тех же коэффициентов

Эти выражения легко получаются при дифференцировании тождеств

138

Пример. Составить выражение второй дифференциальной формы Гаусса дл поверхности заданной уравнением z = f(x,y).

Решение. В данном случае роль параметров играют х и у, поэтому получаются следующие выражения для составляющих радиуса и его производных по параметрам

139

6.3 Кривизна кривой и ее соприкасающаяся плоскость.

Формула (6.4) показывает, что нормальная кривизна линии, проходящей через данную точку поверхности, зависит от направления ее касательной и значения коэффициентов двух форм Гаусса. Коэффициенты обеих квадратичных форм можно вычислить, как только задано уравнение поверхности. В зависимости нормальной кривизны от отношения дифференциалов можно убедиться, разделив числитель и знаменатель в (6.4) на

du2. Отношение dudv характеризует направление касательной к

кривой. Иначе можно утверждать, что все кривые поверхности, проходящие через данную точку и имеющие в ней общую

140

касательную, имеют в этой точке равные между собой нормальные кривизны.

ле этого слова.

Чтобы подчеркнуть ее отличие от нормальной кривизны, будем называть ее полной кривизной. Зависимость между полной и нормальной кривизной получим, вводя угол θ между

нормальным вектором поверхности n и вектором главной нормали кривой.

По определению нормальной кривизны

Таким образом, полная кривизна зависит от нормальной кривизны м угла θ, который совпадает с углом между касательной плоскостью поверхности и соприкасающейся плоскости кривой.

Обратно, если соприкасающаяся плоскость кривой на поверхности, в данной ее точке задана, то она определяет своим пересечением с касательной плоскостью поверхности и касательную прямую данной кривой. Но зная направление касательной прямой, можно найти нормальную кривизну. А так как угол θ тоже известен, то полная кривизна определится. Таким образом, доказано теорема 1:

Полная кривизна кривой, расположенной на поверхности, вполне определяется заданием положения ее соприкасающейся плоскости.

Иначе: все кривые поверхности, имеющие общую точку и общую соприкасающуюся плоскость в этой точке, имеют в ней одинаковые полные кривизны.

141

Полученный результат позволяет свести рассмотрение кривых линий, принадлежащих поверхности к рассмотрению кривизн ее плоских сечений. Действительно, если на поверхности имеется какая угодно кривая (L) и на ней точка M, то проводя плоскость через касательную и главную нормаль к этой кривой в точке М, мы получим в сечении этой плоскости с поверхностью плоскую кривую (L0), имеющую те же касательную и главную нормаль, что и заданная кривая, а потому и тот же радиус кривизны.

6.3.1. Нормальное сечение.

Среди плоских сечений поверхности, проходящих через ее данную точку, нормальными называют те плоскости, которые содержат нормаль к поверхности в этой точке. В этой же точке главная нормаль нормального сечения совпадает с нормалью поверхности. При этом возможны два случая:

1.вектор v главной нормали и вектор n нормали поверхности совпадают;

2.они отличаются знаком.

Так как вектор главной нормами всегда указывает в сторону вогнутости плоской кривой, то в первом случае вектор нормали к поверхности указывает в сторону вогнутости, а во втором в сторону выпуклости нормального сечения. В первом случае нормальное сечение называют вогнутым, а во втором – выпуклым. Свойство вогнутости и выпуклости целиком зависит от выбора направления нормального вектора поверхности и, следовательно, является свойством относительным (рис.45)

142