
- •Оглавление
- •Введение
- •1. Обыкновенные дифференциальные уравнения и системы
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Системы оду. Основные понятия
- •1.3. Связь оду высших порядков и систем оду
- •2.1.2. Уравнения с разделяющимися переменными
- •2.1.3. Однородные уравнения 1-го порядка
- •2.1.4. Уравнения, приводящиеся к однородным
- •2.1.5. Линейные уравнения первого порядка
- •2.1.6. Уравнения Бернулли
- •2.1.7. Уравнения в полных дифференциалах
- •2.2. Обыкновенные дифференциальные уравнения првого порядка. Поведение решений
- •2.2.1. Теорема существования и единственности решения задачи Коши
- •2.2.2. Уравнения первого порядка. Поле направлений
- •2.2.3. Автономные уравнения первого порядка
- •2.2.4. Устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.2.5. Асимптотическая устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.3. Метод изоклин
- •3. Обыкновенные дифференциальные уравнения высших порядков
- •3.1. Обыкновенные дифференциальные уравнения высших порядков. Понижение порядка
- •3.1.1. Понижение порядка обыкновенного дифференциального уравнения. Введение
- •3.1.2. Уравнения, не содержащие независимой переменной
- •3.1.3. Уравнения, не содержащие искомой функции
- •3.1.4. Уравнения с однородной правой частью
- •3.2. Линейные однородные дифференциальные уравнения n-го порядка
- •3.2.1. Линейные однородные дифференциальные уравнения n-го порядка. Введение
- •3.2.2. Свойства решений линейного уравнения. Принцип суперпозиции
- •3.2.3. Существование и единственность решения задачи Коши
- •3.2.4. Линейные уравнения второго порядка. Гармонические колебания
- •3.2.5. Линейные уравнения втрого порядка. Ангармонические колебания
- •3.2.6. Линейные уравнения второго порядка. Уравнение Ньютона
- •3.3. Линейная зависимость и линейная независимость системы функций
- •3.3.1. Линейная зависимость и линейная независимость системы функций
- •3.3.2. Определитель Вронского
- •3.3.3. Исследование линейной независимости системы функций
- •3.3.4. Линейная независимость решений линейного дифференциального уравнения
- •3.4. Структура решения линейного однородного дифференциального уравнения n-го порядка
- •3.4.1. Фундаментальная система решений однородного линейного дифференциального уравнения
- •3.4.2. Структура общего решения линейного однородного уравнения
- •3.4.3. Структура общего решения линейного неоднородного уравнения
- •3.4.4. Метод вариации произвольных постоянных отыскания частного решения
- •3.5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •3.5.1. Решение однородного уравнения с постоянными коэффициентами
- •3.5.2. Метод подбора построения частного решения неоднородного уравнения
- •3.5.3. Уравнение Эйлера
- •4. Системы дифференциальных уравнений
- •4.1. Системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.2. Фазовое пространство. Фазовые траектории
- •4.3. Существование и единственность решения задачи Коши
- •4.4. Интегрирование систем дифференциальных уравнений методом исключения
- •4.4.1. Линейные системы обыкновенных дифференциальных уравнений. Структура
- •4.4.1.1. Линейные системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.4.1.2. Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
- •4.4.1.3. Структура общего решения однородной линейной системы дифференциальных уравнений
- •4.4.1.4. Структура общего решения неоднородной линейной системы дифференциальных уравнений
- •4.4.1.5. Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами методом Эйлера
- •4.4.2. Системы обыкновенных дифференциальных уравнений. Поведение решений
- •4.4.2.1. Устойчивость решений систем дифференциальных уравнений
- •4.4.2.2. Устойчивость и асимптотическая устойчивость по Ляпунову
- •4.4.2.3. Устойчивость положения равновесия линейных систем оду
- •4.4.2.4. Устойчивость точек покоя нелинейных систем по линейному приближению
- •4.4.2.5. Неустойчивость по линейному приближению точек покоя нелинейных систем
- •4.4.3. Автономные системы дифференциальных уравнений
- •4.4.3.1. Автономные системы. Основные понятия
- •4.4.3.2. Свойства фазовых траекторий
- •4.4.3.3. Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы второго порядка
- •4.4.3.4. Векторное поле автономной системы второго порядка
- •4.4.3.5. Точки покоя линейной автономной системы второго порядка с постоянными коэффициентами
- •4.4.4. Численное интегрирование дифференциальных уравнений первого порядка
- •4.4.4.1. Задача Коши. Общие замечания. Постановка задачи
- •4.4.4.2. Метод Эйлера
- •4.4.4.3. Модифицированный метод Эйлера
- •4.4.4.4. Метод Рунге-Кутта
- •2. Решение уравнения модифицированным методом Эйлера:
- •3. Решение уравнения методом Рунге-Кутта:
- •4. Аналитическое решение заданного уравнения:
- •5. Сравнение точного решения и приближенных решений исходного дифференциального уравнения:
- •Библиографический список
- •Обыкновенные дифференциальные уравнения
2.2.4. Устойчивость решений обыкновенных дифференциальных уравнений первого порядка
Любое дифференциальное уравнение или система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс.
Приборы, фиксирующие то или иное физическое явление, не совершенны.
Может оказаться, что малая погрешность измерения начальных данных вызывает «ощутимые» изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление.
И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математическую модель следует признать удачной.
Так возникает важный для приложений вопрос: при каких условиях, математическая модель, описываемая дифференциальными уравнениями, будет устойчивой.
Рассмотрим дифференциальное уравнение
Пусть некоторое фиксированное решение y = φ(x) этого уравнения существует при всех x≥ x0 .
Решение y = φ(x) уравнения называется устойчивым по Ляпунову при x ≥ x0 , если для любого ε > 0 существует число δ > 0 (зависящее, вообще говоря, от ε) такое, что:
– решение y = y(x) задачи Коши с начальным условием y(x0), |y(x0) − φ(x0) | < δ, существует при всех x ≥ x0 ;
– для всех таких решений справедливо неравенство |y(x) − φ(x) | < ε , при всех x > x0 .
Геометрически это означает, что интегральные кривые y = y(x), близкие в момент x = x0 к интегральной кривой y = φ(x), остаются близкими к ней и на всем промежутке [x0, ∞) .
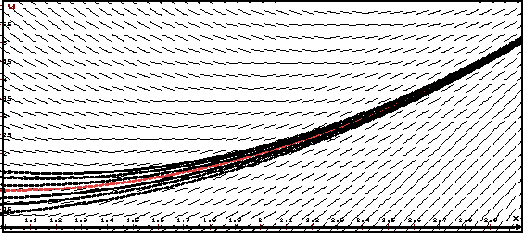
На рисунке красным изображено устойчивое решение задачи Коши y' = − y, y(1) = 1.
Видно, что все интегральные кривые, близкие к этому решению в начальный момент x = 1, остаются вблизи него и при x > 1 .
Решение y = φ(x) называется неустойчивым по Ляпунову при x ≥ x0 , если существует число ε > 0 такое, что для любого δ > 0
найдутся решения y = yδ(x) и значение x1 = x1(δ) > x0 такие, что хотя | yδ( x0) − φ( x0) | < δ , но |y( x1) − φ( x1) | ≥ ε .
На рисунке красным изображено неустойчивое решение y = 0 задачи Коши y' = sin2 y, y(0) = 0.
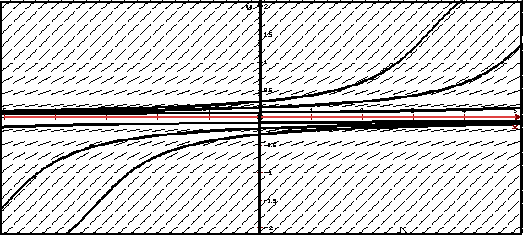
Видно, что интегральные кривые, близкие к y = 0 в начальный момент x0 = 0, удаляются от y = 0 с ростом x > 1 .
Пример №1
Геометрически устойчивость решения дифференциального уравнения, удовлетворяющего условию y(x0) = y0 , y = φ(x), φ(x0)= y0, означает, что интегральные кривые y = y(x), близкие к интегральной кривой y = φ(x) в момент x = x0 , остаются близкими к ней и на всем промежутке [x0, ∞) .
На рисунке красным изображено устойчивое решение задачи Коши y' = − y, y(1) = 1. Видно, что все интегральные кривые, близкие к этому решению в начальный момент x = 1, остаются вблизи него и при x >1 .
Устойчивость решения можно доказать аналитически.
Легко видеть, что общее решение уравнения y' = − y , имеет вид y =
=Cexp(− x). Решением задачи Коши y' = − y, y(1) = 1 является функция φ(x) = exp(1 − x),
а решение задачи Коши y' = − y, y(1) = y0 − функция y(x) = y0 exp(1 − x). Все эти решения существуют при x ≥ 1.
Возьмём произвольное ε > 0 и положим δ = ε.
Тогда, если |y(x0) − φ(x0) | = | y0 − 1 | < δ , то при всех x >1
|y(x) − φ(x) | = | y0 exp(1 − x) − exp(1 − x) | = | y0− 1 |· exp(1 − x) < | y0− 1 | < δ = ε ,
т.е. действительно, как показано на рисунке, решение φ(x) = exp(1 − x) устойчиво по Ляпунову.
Пример №2
На рисунке красным изображено неустойчивое решение y = 0 задачи Коши y' = sin2 y, y(0) = 0.
Легко видеть, что функция y = 0 − решение задачи Коши y' = sin2 y , y(0) = 0, что при x ≥ 0 существует общее решение уравнения y' = sin2 y, которое имеет вид y = arcctg(x +C), и что решением задачи Коши y' = sin2 y , y(0) =y0 является функция y(x) = arcctg(x + ctg y0).
Положим ε = π/2. При x → ∞ справедливо
|y(x) − φ(x) | = |arcctg(x + ctg y0)− 0 | = |arcctg(x + ctg y0) | → π.
Но тогда, как бы ни было мало δ > 0 такое, что
|y(x0) − φ(x0) | = |y(0) − φ(0) | = |y0− 0 | = | y0 | < δ ,
найдётся такое x1 > 0, что при всех x >x1
|y(x) − φ(x) | > π/2 = ε .
Таким образом, мы показали аналитически, что решение y = 0 − неустойчивое решение уравнения.
