
- •Оглавление
- •Введение
- •1. Обыкновенные дифференциальные уравнения и системы
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Системы оду. Основные понятия
- •1.3. Связь оду высших порядков и систем оду
- •2.1.2. Уравнения с разделяющимися переменными
- •2.1.3. Однородные уравнения 1-го порядка
- •2.1.4. Уравнения, приводящиеся к однородным
- •2.1.5. Линейные уравнения первого порядка
- •2.1.6. Уравнения Бернулли
- •2.1.7. Уравнения в полных дифференциалах
- •2.2. Обыкновенные дифференциальные уравнения првого порядка. Поведение решений
- •2.2.1. Теорема существования и единственности решения задачи Коши
- •2.2.2. Уравнения первого порядка. Поле направлений
- •2.2.3. Автономные уравнения первого порядка
- •2.2.4. Устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.2.5. Асимптотическая устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.3. Метод изоклин
- •3. Обыкновенные дифференциальные уравнения высших порядков
- •3.1. Обыкновенные дифференциальные уравнения высших порядков. Понижение порядка
- •3.1.1. Понижение порядка обыкновенного дифференциального уравнения. Введение
- •3.1.2. Уравнения, не содержащие независимой переменной
- •3.1.3. Уравнения, не содержащие искомой функции
- •3.1.4. Уравнения с однородной правой частью
- •3.2. Линейные однородные дифференциальные уравнения n-го порядка
- •3.2.1. Линейные однородные дифференциальные уравнения n-го порядка. Введение
- •3.2.2. Свойства решений линейного уравнения. Принцип суперпозиции
- •3.2.3. Существование и единственность решения задачи Коши
- •3.2.4. Линейные уравнения второго порядка. Гармонические колебания
- •3.2.5. Линейные уравнения втрого порядка. Ангармонические колебания
- •3.2.6. Линейные уравнения второго порядка. Уравнение Ньютона
- •3.3. Линейная зависимость и линейная независимость системы функций
- •3.3.1. Линейная зависимость и линейная независимость системы функций
- •3.3.2. Определитель Вронского
- •3.3.3. Исследование линейной независимости системы функций
- •3.3.4. Линейная независимость решений линейного дифференциального уравнения
- •3.4. Структура решения линейного однородного дифференциального уравнения n-го порядка
- •3.4.1. Фундаментальная система решений однородного линейного дифференциального уравнения
- •3.4.2. Структура общего решения линейного однородного уравнения
- •3.4.3. Структура общего решения линейного неоднородного уравнения
- •3.4.4. Метод вариации произвольных постоянных отыскания частного решения
- •3.5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •3.5.1. Решение однородного уравнения с постоянными коэффициентами
- •3.5.2. Метод подбора построения частного решения неоднородного уравнения
- •3.5.3. Уравнение Эйлера
- •4. Системы дифференциальных уравнений
- •4.1. Системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.2. Фазовое пространство. Фазовые траектории
- •4.3. Существование и единственность решения задачи Коши
- •4.4. Интегрирование систем дифференциальных уравнений методом исключения
- •4.4.1. Линейные системы обыкновенных дифференциальных уравнений. Структура
- •4.4.1.1. Линейные системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.4.1.2. Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
- •4.4.1.3. Структура общего решения однородной линейной системы дифференциальных уравнений
- •4.4.1.4. Структура общего решения неоднородной линейной системы дифференциальных уравнений
- •4.4.1.5. Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами методом Эйлера
- •4.4.2. Системы обыкновенных дифференциальных уравнений. Поведение решений
- •4.4.2.1. Устойчивость решений систем дифференциальных уравнений
- •4.4.2.2. Устойчивость и асимптотическая устойчивость по Ляпунову
- •4.4.2.3. Устойчивость положения равновесия линейных систем оду
- •4.4.2.4. Устойчивость точек покоя нелинейных систем по линейному приближению
- •4.4.2.5. Неустойчивость по линейному приближению точек покоя нелинейных систем
- •4.4.3. Автономные системы дифференциальных уравнений
- •4.4.3.1. Автономные системы. Основные понятия
- •4.4.3.2. Свойства фазовых траекторий
- •4.4.3.3. Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы второго порядка
- •4.4.3.4. Векторное поле автономной системы второго порядка
- •4.4.3.5. Точки покоя линейной автономной системы второго порядка с постоянными коэффициентами
- •4.4.4. Численное интегрирование дифференциальных уравнений первого порядка
- •4.4.4.1. Задача Коши. Общие замечания. Постановка задачи
- •4.4.4.2. Метод Эйлера
- •4.4.4.3. Модифицированный метод Эйлера
- •4.4.4.4. Метод Рунге-Кутта
- •2. Решение уравнения модифицированным методом Эйлера:
- •3. Решение уравнения методом Рунге-Кутта:
- •4. Аналитическое решение заданного уравнения:
- •5. Сравнение точного решения и приближенных решений исходного дифференциального уравнения:
- •Библиографический список
- •Обыкновенные дифференциальные уравнения
3.3. Линейная зависимость и линейная независимость системы функций
3.3.1. Линейная зависимость и линейная независимость системы функций
Функции y1(x), y2(x), ..., yn(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α1, α2, ..., αn, не равные нулю одновременно и такие, что
α1y1(x) + α2y2(x) + ... + αnyn(x) = 0
для всех x из отрезка [a;b].
В противном случае функции y1(x), y2(x), ..., yn(x) называются линейно независимыми.
Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.
Справедливо следующее утверждение.
Функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке.
Очевидны следующие утверждения.
• Если среди функций y1(x), y2(x), ..., yn(x) есть нулевая функция, то функции линейно зависимы.
• Если функции y1(x), y2(x), ..., yk(x) линейно зависимы, то при любых yk + 1(x), yk + 2(x), ..., yn (x) функции y1(x), y2(x), ..., yk(x), yk + 1(x), ..., yn(x) также линейно зависимы.
• Если функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри [a;b] .
• Если функции y1(x), y2(x), ..., yn(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок [а;b] (если, они определены на этом отрезке).
Вектор-функции Y1(x), Y2(x), ..., Yn(x),
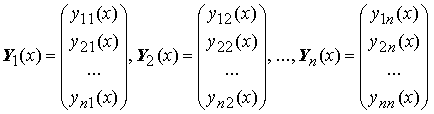
называются линейно зависимыми на отрезке [a;b] , если существуют постоянные α1, α2, ..., αn , не равные нулю одновременно и такие, что
α1Y1(x) + α2Y2(x) + ... + αnYn(x) = 0
для всех x из отрезка [a;b].
В противном случае функции Y1(x),Y2(x), ..., Yn(x) называются линейно независимыми.
Пример №1
Докажем линейную независимость на всей числовой оси функций 1, x, x2,..., xn.
Допустим противное, т.е. допустим, что существуют постоянные α1, α2, ..., αn+1 , не равные нулю одновременно и такие, что для всех x справедливо
α1·1 + α2·x + ... + αn+1·xn = 0.
Последнее равенство для всех x возможно тогда и только тогда, когда многочлен α1·1 + α2·x + ... + αn+1·xn тожественно равен нулю, т.е. тогда и только тогда, когда
α1= α2= ... = αn+1= 0.
Это последнее равенство противоречит предположению что постоянные α1, α2, ..., αn+1 , не равны нулю одновременно. Утверждение доказано.
Пример №2
Докажем линейную зависимость на всей числовой оси функций sin2x, cos2x, 1.
Поскольку
sin2x + cos2x = 1, то
sin2x + cos2x − 1 = 0, т.е.
1·sin2x + 1·cos2x + (− 1)·1 = 0,
коэффициенты линейной комбинации не равны нулю, и, следовательно, функции sin2x, cos2x, 1 линейно зависимы. Утверждение доказано.
Пример №3
Докажем линейную независимость на всей числовой оси функций
![]()
Докажем утверждение по индукции.
Пусть утверждение справедливо для k = 1:
![]()
Предположим теперь, что линейная независимость доказана для k − 1 функций
![]()
А для k функций
![]()
допустим противное, т.е. допустим, что существуют постоянные α1, α2, ..., αk , не равные нулю одновременно и такие, что для всех x справедливо
![]()
Разделим обе части равенства на exp(λkx)
![]()
и продифференцируем последнее тождество по x:
![]()
Но входящие в равенство k − 1 функции по нашему индуктивному предположению линейно независимы и λi − λk ≠ 0. Следовательно, последнее равенство возможно, только если все, входящие в него коэффициенты равны нулю:
α1= α2= ... = αk− 1= 0.
Но тогда
![]()
и
α1= α2= ... = αk= 0.
Получили противоречие (предполагалось, что не все коэффициенты равны нулю). Это противоречие доказывает линейную независимость k функций. А отсюда, в свою очередь, по индукции следует линейная независимость всей исследуемой системы функций.
