
- •Оглавление
- •Введение
- •1. Обыкновенные дифференциальные уравнения и системы
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Системы оду. Основные понятия
- •1.3. Связь оду высших порядков и систем оду
- •2.1.2. Уравнения с разделяющимися переменными
- •2.1.3. Однородные уравнения 1-го порядка
- •2.1.4. Уравнения, приводящиеся к однородным
- •2.1.5. Линейные уравнения первого порядка
- •2.1.6. Уравнения Бернулли
- •2.1.7. Уравнения в полных дифференциалах
- •2.2. Обыкновенные дифференциальные уравнения првого порядка. Поведение решений
- •2.2.1. Теорема существования и единственности решения задачи Коши
- •2.2.2. Уравнения первого порядка. Поле направлений
- •2.2.3. Автономные уравнения первого порядка
- •2.2.4. Устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.2.5. Асимптотическая устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.3. Метод изоклин
- •3. Обыкновенные дифференциальные уравнения высших порядков
- •3.1. Обыкновенные дифференциальные уравнения высших порядков. Понижение порядка
- •3.1.1. Понижение порядка обыкновенного дифференциального уравнения. Введение
- •3.1.2. Уравнения, не содержащие независимой переменной
- •3.1.3. Уравнения, не содержащие искомой функции
- •3.1.4. Уравнения с однородной правой частью
- •3.2. Линейные однородные дифференциальные уравнения n-го порядка
- •3.2.1. Линейные однородные дифференциальные уравнения n-го порядка. Введение
- •3.2.2. Свойства решений линейного уравнения. Принцип суперпозиции
- •3.2.3. Существование и единственность решения задачи Коши
- •3.2.4. Линейные уравнения второго порядка. Гармонические колебания
- •3.2.5. Линейные уравнения втрого порядка. Ангармонические колебания
- •3.2.6. Линейные уравнения второго порядка. Уравнение Ньютона
- •3.3. Линейная зависимость и линейная независимость системы функций
- •3.3.1. Линейная зависимость и линейная независимость системы функций
- •3.3.2. Определитель Вронского
- •3.3.3. Исследование линейной независимости системы функций
- •3.3.4. Линейная независимость решений линейного дифференциального уравнения
- •3.4. Структура решения линейного однородного дифференциального уравнения n-го порядка
- •3.4.1. Фундаментальная система решений однородного линейного дифференциального уравнения
- •3.4.2. Структура общего решения линейного однородного уравнения
- •3.4.3. Структура общего решения линейного неоднородного уравнения
- •3.4.4. Метод вариации произвольных постоянных отыскания частного решения
- •3.5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •3.5.1. Решение однородного уравнения с постоянными коэффициентами
- •3.5.2. Метод подбора построения частного решения неоднородного уравнения
- •3.5.3. Уравнение Эйлера
- •4. Системы дифференциальных уравнений
- •4.1. Системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.2. Фазовое пространство. Фазовые траектории
- •4.3. Существование и единственность решения задачи Коши
- •4.4. Интегрирование систем дифференциальных уравнений методом исключения
- •4.4.1. Линейные системы обыкновенных дифференциальных уравнений. Структура
- •4.4.1.1. Линейные системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.4.1.2. Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
- •4.4.1.3. Структура общего решения однородной линейной системы дифференциальных уравнений
- •4.4.1.4. Структура общего решения неоднородной линейной системы дифференциальных уравнений
- •4.4.1.5. Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами методом Эйлера
- •4.4.2. Системы обыкновенных дифференциальных уравнений. Поведение решений
- •4.4.2.1. Устойчивость решений систем дифференциальных уравнений
- •4.4.2.2. Устойчивость и асимптотическая устойчивость по Ляпунову
- •4.4.2.3. Устойчивость положения равновесия линейных систем оду
- •4.4.2.4. Устойчивость точек покоя нелинейных систем по линейному приближению
- •4.4.2.5. Неустойчивость по линейному приближению точек покоя нелинейных систем
- •4.4.3. Автономные системы дифференциальных уравнений
- •4.4.3.1. Автономные системы. Основные понятия
- •4.4.3.2. Свойства фазовых траекторий
- •4.4.3.3. Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы второго порядка
- •4.4.3.4. Векторное поле автономной системы второго порядка
- •4.4.3.5. Точки покоя линейной автономной системы второго порядка с постоянными коэффициентами
- •4.4.4. Численное интегрирование дифференциальных уравнений первого порядка
- •4.4.4.1. Задача Коши. Общие замечания. Постановка задачи
- •4.4.4.2. Метод Эйлера
- •4.4.4.3. Модифицированный метод Эйлера
- •4.4.4.4. Метод Рунге-Кутта
- •2. Решение уравнения модифицированным методом Эйлера:
- •3. Решение уравнения методом Рунге-Кутта:
- •4. Аналитическое решение заданного уравнения:
- •5. Сравнение точного решения и приближенных решений исходного дифференциального уравнения:
- •Библиографический список
- •Обыкновенные дифференциальные уравнения
3.1.4. Уравнения с однородной правой частью
Если правая часть уравнения
F(x, y, y ',..., y(n)) = 0,
удовлетворяет условию однородности
F(x, ty, ty ',..., ty(n) ) = tk F(x, y, y ',..., y(n) )
то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных.
Если в результате каких-либо преобразований порядок n уравнения F(x, y, y ',..., y(n)) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.
К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных.
Порядок такого уравнения можно понизить заменой
![]()
Выражение для первой производной от y(x) не содержит производной от z(x):
![]()
Поэтому, заменив в исходном уравнении y, y ',..., y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка.
Рассмотрим, например, уравнение третьего порядка, однородное относительно неизвестной функции и всех ее производных:
F(x, y, y', y'', y''') = 0,
F(x, y, y', y'', y''') = tk F(x, y, y', y'', y''').
Посмотрим, как прядок такого уравнения можно понизить до второго, используя замену
Выразим y', y'', y''' через z(x):

Произведя замену, получим дифференциальное уравнение второго порядка:
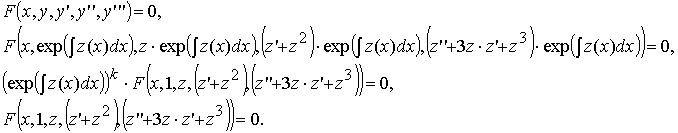
В итоге получено дифференциальное уравнение второго порядка относительно z(x):
Φ(x, z, z', z'') = 0.
Пример №1
Решим обыкновенное дифференциальное уравнение 2-го порядка
yy'+ x(y')2 + xyy'' = 0.
Легко видеть, что это уравнение, однородно относительно неизвестной функции и всех ее производных:
(ty)(ty')+ x((ty'))2 + x(ty)(ty'') = t2 (yy'+ x(y')2 + xyy'')
Используем стандартную для таких уравнений замену
Выполним замену:
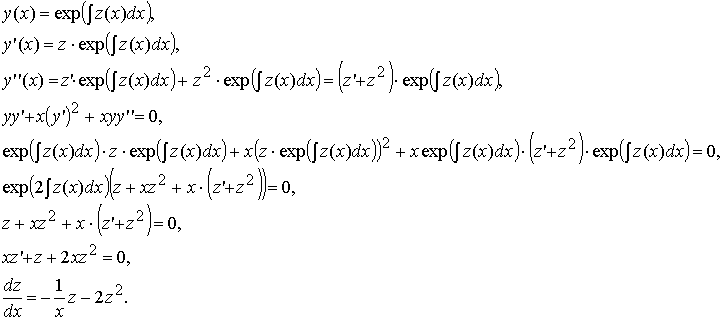
Получили уравнение первого порядка
![]()
Это уравнение Бернулли, которое интегрируется стандартным для уравнений Бернулли способом.
3.2. Линейные однородные дифференциальные уравнения n-го порядка
3.2.1. Линейные однородные дифференциальные уравнения n-го порядка. Введение
Линейным дифференциальным уравнением n-го порядка называется уравнение вида
y(n) + an-1(x)y(n -1) + ... + a1(x)y' + a0(x)y = f(x).
Коэффициенты уравнения an-1(x), an-2(x), ..., a1(x), a0(x) и правую часть f(x) полагаем непрерывными на отрезке [a;b] .
y(n) + an-1(x)y(n-1) + ... + a1(x)y' + a0(x)y = f(x)
– неоднородное линейное дифференциальное уравнение n-го порядка,
y(n) + an-1(x)y(n-1) + ... + a1(x)y' + a0(x)y = 0
– однородное линейное дифференциальное уравнение n-го порядка,
Выражение в левой части уравнения называется линейным дифференциальным оператором n-го порядка:
L(y) ≡ y(n) + an-1(x)y(n-1) + ... + a1(x)y' + a0(x)y.
L(y) = 0 и L(y) = f(x) – соответственно однородное и неоднородное уравнения в операторной записи.
При изучении линейных дифференциальных уравнений используются пространства C[a;b] – пространство непрерывных на отрезке [a;b] функций, и Ck [a;b] – пространство функций, непрерывных на [a;b] , вместе со своими производными до k-го порядка включительно.
