2.3. Дифференциальные уравнения равновесия Эйлера

Какова зависимость гидростатического давления в жидкости от координат трехмерного пространства? Для ответа на данный вопрос предположим, что покоящаяся жидкость находится в поле сил давления и тяжести. Выделим в жидкости элементарный параллелепипед объемом , ориентируя его ребра вдоль координатных осей (рис. 2.4). Априори можно считать, что давление одновременно зависит от трех координат, поэтому на параллельных гранях параллелепипеда оно различно. Например, на нижней грани давление равно p, а на верхней .

Рис. 2.4

Воспользуемся основным принципом статики: сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. Сумма проекций на ось х:

.

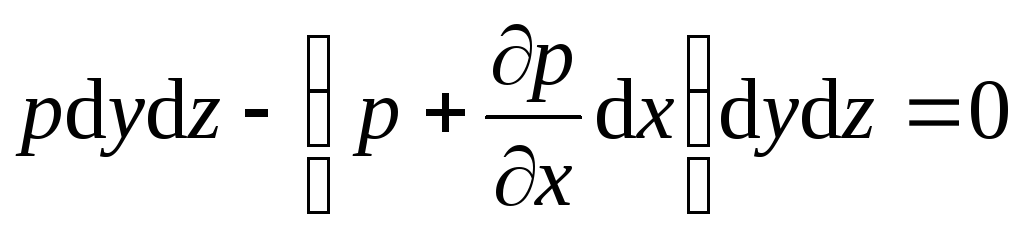Для оси у

.

Для оси z

,

где , – плотность жидкости.

После упрощений с учетом имеем

(2.3)

Полученная система (2.3) отвечает на поставленный вопрос и называется дифференциальными уравнениями равновесия Эйлера.

2.4. Основное уравнение гидростатики

Из уравнений равновесия Эйлера (2.3) следует, что давление изменяется только по вертикали, оставаясь одинаковым во всех точках любой горизонтальной плоскости, т. е. изменения давления вдоль осей х и у равны нулю. Итак, гидростатическое давление является функцией только аппликаты z (cм. рис. 2.4). Каков вид данной функции? Установим это. В связи с тем, что в системе (2.3) частные производные и равны нулю, частная производная может быть заменена полной производной , поэтому получаем

.

Отсюда следует

.

Для несжимаемой однородной жидкости плотность постоянна, поэтому

или .

После интегрирования получаем

. (2.4)

Если выбрать две произвольные горизонтальные плоскости, то уравнение (2.4) примет вид

. (2.5)

В формуле (2.5) z₁ и z₂ – высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения); p₁ и p₂ – гидростатическое давление в этих точках. Нетрудно установить, что слагаемые и так же, как z₁ и z₂, измеряются в метрах. Поэтому величина названа напором давления, или пьезометрическим напором. Величины z₁ и z₂ названы нивелирными высотами и отсчитываются от плоскости сравнения.

Геометрический смысл уравнения (2.5) заключается в том, что для каждой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная. Члены уравнения (2.5) имеют также определенный энергетический смысл. Из анализа размерностей слагаемых z и получается, что эти величины характеризуют энергию_t приходящуюся на единицу веса жидкости . Поэтому нивелирная высота характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения, а пьезометрический напор – удельную потенциальную энергию давления в рассматриваемой точке. Сумма указанных энергий, называемая полным гидростатическим напором (статическим напором), равна общей потенциальной энергии, приходящейся на единицу веса жидкости. Следовательно, (2.5) – частный случай закона сохранения энергии: удельная потенциальная энергия есть величина постоянная.

Как было указано, нивелирная высота отсчитывается вверх от плоскости сравнения. Это неудобно для проведения практических расчетов, так как чаще говорят о глубине погружения тела в жидкость, а не, например, о расстоянии между телом и дном. Поэтому преобразуем формулу (2.5). Допустим, что нужно найти давление в точке 1, погруженной в жидкость на глубину h (рис. 2.5).

Выберем плоскостью сравнения 0–0 днище сосуда; параллельно ей проведем плоскости I–I и II–II соответственно через точку 1 и свободную поверхность жидкости. При давлении на свободную поверхность p₀ формула (2.5) примет вид

.

Отсюда . Учитывая, что , получаем

. (2.6)

Формулы (2.4), (2.5) и (2.6) называются основным уравнением гидростатики. Оно устанавливает связь между вертикальной координатой трехмерного пространства и давлением. Из этого уравнения следует, что гидростатическое давление является линейной функцией аппликаты. Величина p₁ в формуле (2.6) называется абсолютным гидростатическим давлением в точке 1. Оно равно абсолютному давлению на свободной поверхности p₀, сложенному с гидростатическим (весовым) давлением , обусловленным весом самой жидкости.

Разность между абсолютным и атмосферным давлением называется избыточным (манометрическим) давлением: . Разность между атмосферным и абсолютным давлениями называется вакуумом: .