Расчет длинных трубопроводов

Решим задачи нахождения потерь напора по длине и расхода жидкости, полагая, что длинные трубопроводы работают в квадратичной зоне сопротивления.

Простой длинный трубопровод

Возможны два случая работы такого трубопровода: работа под уровень и работа в атмосферу.

а) Работа под уровень. Такой случай показан на рис. 3.32. Пусть полная длина трубопровода равна l, а диаметр – d. Выберем плоскость сравнения 0–0, как показано на рис. 3.32, и запишем уравнение Бернулли для сечений I–I и II–II

.

Если площади резервуаров велики, то скорости движения W₁ и W₂ малы и ими можно пренебречь. Кроме этого, очевидно, что . Поэтому уравнение Бернулли упростится: где Н – разность уровней в резервуарах. Значит, величина Н расходуется на преодоление гидравлического сопротивления трубопровода. Определив таким путем , можно найти расход жидкости по формуле (3.68)

.

б) Работа в атмосферу. Такой трубопровод изображен иа рис. 3.33. Пусть трубопровод состоит из трех участков труб с диаметрами d₁, d₂, d₃, длиной l₁, l₂, l₃. Применим формулу (3.69) для каждого из участков трубопровода:

Рис. 3.33

Общие потери напора равны сумме найденных потерь

,

или

.

Если обозначить 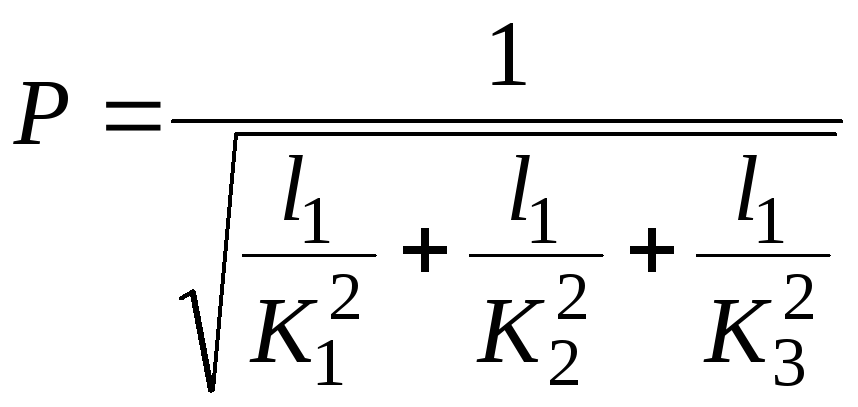, то По этой формуле находят при известном расходе Q. Если известны потери напора , а требуется найти Q, то очевидно равенство: . Здесь и в предыдущем равенстве величина Р – проводимость трубопровода.

Сложный длинный трубопровод

а) Параллельное соединение труб. Допустим, что из точки А в точку В подается жидкость в количестве Q без раздачи по пути. В узле а трубопровод разделяется на три паралледьные линии, а в узле b они соединяются (рис. 3.34). Длины параллельных участков равны l₁, l₂, l₃, а их диаметры – d₁, d₂, d₃.

Рис. 3.34

Задача 1. Найти объемные расходы q₁, q₂, q₃ по параллельным линиям.

В точках а и b напоры для всех трех линий одинаковы, поэтому в них одинаковы потери напора и составляют . Тогда имеем

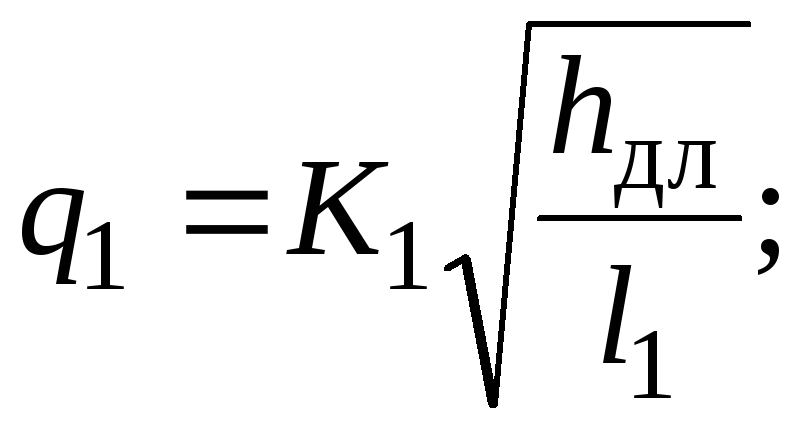
(3.70)

Отсюда

,

или

Потери напора равны

Далее по формулам (3.70) находят величины q₁, q₂, q₃.

Задача 2. Найти диаметры d₁, d₂, d₃, при которых выполняется условие q₁ = q₂ = q₃. Из формулы (3.70) следует, что требуемое равенство расходов выполняется при Данную задачу решают подбором, пользуясь таблицей значений .

б) Разветвленные трубопроводы. Пусть трубопровод, начинающийся в точке А, делится в узле В на две ветви: ВС и ВD (рис. 3.35). Требуется найти расходы в точках С и D, если известны напор в точке А, диаметры труб и длины участков.

Для решения данной и подобной задач используют графоаналитический метод. Он заключается в построении характеристик отдельных участков трубопровода и суммарной характеристики всего трубопровода. Характеристикой трубопровода называется график зависимости при и ; ее можно построить на основе зависимости (3.65) Сначала строят характеристики для ветвей ВС и BD, т. е. и , а затем для участка АВ, т. е. (см. рис. 3.36). Так как в точке В напор одинаков для ветвей ВС и ВD, то общую характеристику участков ВС и ВD получают сложением абсциcc характеристик этих участков, выбрав ряд значений , а именно: . Расход начального участка АВ равен сумме расходов ветви ВС и ВD: Q_A = Q_D + Q_C. Поэтому нужно сложить ординаты характеристики и характеристики начального участка , выбрав ряд значений расхода. В результате получают суммарную характеристику трубопровода , позволяющую определить пропускную способность трубопровода и его ветвей при заданном напоре Н. Для этого по суммарной характеристике трубопровода определяют расход, соответствующий заданному напору, а затем по суммарной характеристике ветвей ВС и ВD устанавливают распределение этого расхода по указанным ветвям трубопровода (см. рис. 3.36).

h_дл= f₁(Q_D)

H = f₅(Q_A)

h_дл= f₃(Q_A)

h_дл= f₂(Q_C)

h_дл

H

h_дл= f₄(Q_D+Q_C)

Q_D

Q_C

Q_D+Q_C

Q

Рис. 3.36

Примечание. При работе трубопровода в неквадратичной зоне сопротивления используют те же зависимости, что и для квадратичной зоны сопротивления, но в расчетные формулы вводят поправочный коэффициент на неквадратичность. Здесь λ – действительный коэффициент гидравлического трения трубопровода; – коэффициент гидравлического трения того же трубопровода в квадратичной зоне трения.