1.2. Силы, действующие в жидкости Понятие об идеальной жидкости

Силы, действующие в жидкости, подразделяются на объемные (массовые) и поверхностные. Объемные силы пропорциональны объему (массе) жидкости (к ним относятся сила тяжести, сила инерции), а поверхностные силы пропорциональны площади поверхности, на которую они действуют (например, сила атмосферного давления на поверхность жидкости в открытом сосуде, сила вязкости).

При выводе основных закономерностей в гидравлике вводят понятие о гипотетической идеальной жидкости, которая, в отличие от реальной (вязкой) жидкости, абсолютно несжимаема под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью. Использование понятия об идеальной жидкости существенно упрощает решение многих задач гидродинамики, а справедливость полученных зависимостей проверяется и устанавливается проведением гидравлических экспериментов. В гидростатике понятия об идеальной и реальной жидкости совпадают.

Глава 2. Гидростатика

2.1. Гидростатическое давление

В предыдущей главе указывалось, что в гидростатике изучаются условия равновесия жидкостей. Рассмотрим некоторый объем жидкого тела, находящегося в равновесии (рис. 2.1).

Разделим плоскостью АВ данный объем на 2 части. Обозначим площадь плоскости раздела через S, и мысленно отбросим часть объема I. Тогда для сохранения равновесия оставшейся части II заменим воздействие на нее со стороны части I силой Р. Эта сила называется силой гидростатического давления на площадку S. Разделив силу гидростатического давления на величину площади S, получим среднее гидростатическое давление р_ср = P/S. Пусть в плоскости АВ имеется точка С; выделим возле нее элементарную площадку ΔS. Сила, действующая на эту площадку – ΔР. Добиваясь ΔS получим предел отношения силы ΔР к площадке ΔS, называемый давлением в точке

. (2.1)

2.2. Свойства гидростатического давления

Первое свойство: гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую это давление действует. Доказательство производим методом от противного. Рассмотрим некоторый объем жидкости в состоянии равновесия (рис. 2.2).

Разделим объем произвольно на две части плоскостью S–S. На поверхности раздела возьмем точку А и предположим, что гидростатическое давление в ней направлено не по нормали к площадке, на которой расположена точка А. Тогда вектор гидростатического давления можно разложить на две составляющие – на нормальную р_н и касательную р_к. Существование касательной составляющей давления р_к приведет к тому, что жидкость выйдет из равновесия, т. е. нарушится исходная предпосылка о равновесии жидкости. Значит, единственно возможным является нормальное действие г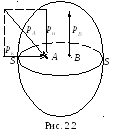идростатического давления на выбранную площадку. Докажем теперь, что гидростатическое давление может быть направлено только по внутренней нормали. Предположим, что оно направлено по внешней нормали, как на рис. 2.2 в точке В. В этом случае возникновение растягивающей силы гидростатического давления вызвало бы появление касательных напряжений. Тогда жидкость пришла бы в движение, что опять противоречит условию о равновесии.

Следовательно, единственно возможным направлением гидростатического давления является направление по внутренней нормали.

Второе свойство: величина гидростатического давления в любой точке жидкости по всем направлениям одинакова.

Выделим в покоящейся жидкости около точки А бесконечно малую призму со сторонами dx, dy и dz (рис 2.3.). Рассмотрим условия равновесия этой призмы. Покажем внешние силы, действующие на поверхности призмы – силы гидростатического давления . Определим эти силы. Если р_z – средние гидростатические давления на соответствующих сторонах призмы, то ; ; . К внешним силам относятся и объемные силы (тяжести и центробежная). Обозначим через равнодействующую всех объемных сил, отнесенную к единице массы. Тогда на призму действует равнодействующая всех объемных сил, равная , где М – масса призмы. Объем призмы равен , и при плотности жидкости ρ масса призмы составит , а равнодействующая будет . Сопоставляя объемные силы с силами гидростатического давления , приходим к выводу, что объемные силы на порядок меньше сил давления, поэтому объемными силами можно пренебречь.

Рис. 2.3

Для того, чтобы призма находилась в равновесии, сумма проекций на любую ось всех сил, действующих на призму, должна быть равна нулю. Спроектировав силы на оси х и z, получаем ; или ; .

Из рис. 2.3 видно, что и , поэтому имеем ; или

. (2.2)

Получили, что гидростатическое давление в исследуемой точке А одинаково по всем направлениям (так как направление п было взято нами произвольно).