3.13. Профиль скорости в живом сечении потока при турбулентном режиме движения

Нахождение профиля истинной скорости в турбулентном потоке является сложной и пока еще не решенной задачей гидравлики и гидромеханики. Однако, если бы такая зависимость существовала, она была бы, несомненно, весьма сложной и воспользоваться ею было бы крайне затруднительно. Кроме истинной скорости, турбулентный поток характе-ризуется осредненной скоростью (см. разд. 3.12), профиль которой, как показывают опытные данные, отличается от профиля скорости при ламинарном режиме (ср. рис. 3.21 и 3.20). Какой математической зависимостью описывается профиль осредненной скорости в канале на рис. 3.21? Точный ответ на данный вопрос пока не найден, а первым и наиболее известным является решение, полученное на основе полуэмпирической теории Л. Прандтля. Ниже излагаются основы этой теории. Выделим в жидкости два слоя А и В, имеющие площадь взаимного соприкосновения S. Скорость движения слоя А равна (рис. 3.23). Покажем направление отсчета поперечной координаты h и запишем напряжение внутреннего трения по закону Ньютона (1.8): . При турбулентном движении, кроме продольного движения, имеется поперечное перемещение частиц со скоростью . Под влиянием этой скорости из слоя В в слой А переместится масса жидкости , и это вызывет появление касательной силы , a касательное напряжение при этом составит . Л. Прандтль предложил определить скорости W_А и W_B следующим образом:

и ,

где и – коэффициенты пропорциональности. Воспользовавшись этими зависимостями, находим

,

где величина названа длиной пути перемешивания Прандтля. Суммарные касательные напряжения равны

. (3.47)

Экспериментальные исследования показывают, что первый член мал по сравнению со вторым слагаемым формулы (3.47). Величина выражает вязкостное трение, а член характеризует трение при перемешивании. Л. Прандтль не предложил метода расчета длины пути перемешивания l, однако на основании опытных данных установлено, что между величиной l и расстоянием от стенки h существует примерно пропорциональная зависимость , где k – коэффициент пропорциональности (универсальная постоянная). Считая, что , из (3.47) получим

или

Отсюда

Вблизи стенки касательное напряжение можно заменить постоянным по величине касательным напряжением на стенке ; тогда имеем

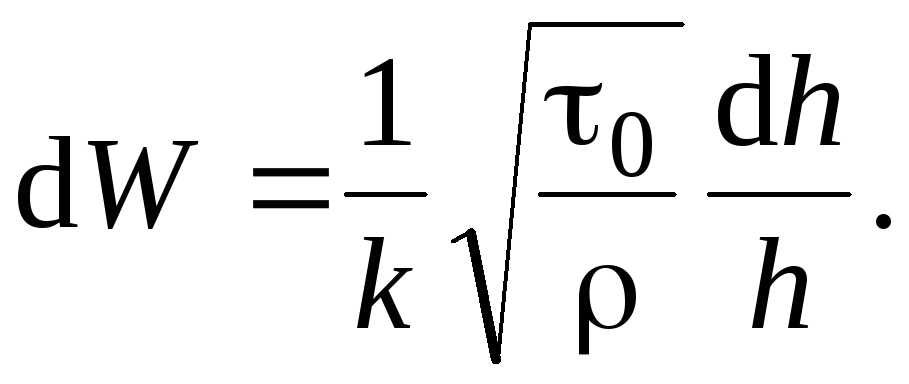
Величина имеет размерность скорости и называется динамической скоростью . Интегрирование дает

. (3.48)

Постоянную интегрирования С находим из условия: при (на оси потока) величина , где – радиус трубы; – расстояние, отсчитываемое по нормали от стенки труби. Тогда

и .

После подстановки найденной постоянной в уравнение (3.48) имеем

,

или

. (3.49)

Из зависимости (3.49) следует, что осредненная скорость изменяется по логарифмическому закону. Формула (3.49) справедлива для пристенной области турбулентного потока, но ее можно распространить, со значительными допущениями, на поток жидкости в целом. Для этого полагают, что хотя экспериментальные исследования показывают, что не является постоянной величиной. С учетом этого, после перехода к десятичным логарифмам, зависимость (3.49) примет вид

. (3.50)

Полученная формула (3.50) является искомой и позволяет определить, с некоторой долей приближения, осредненные скорости в различных точках сечения трубы.