3.10. Виды гидравлических сопротивлений

Потери напора при движении жидкости по трубопроводам обусловлены сопротивлением по длине (трения) h_дл и местным сопротивлением h_мс. Сопротивление h_дл существует при движении жидкости по всей длине трубопровода, так как оно обусловлено наличием сил трения в самой жидкости, а также силами трения жидкости о стенки трубопровода. Местные сопротивления возникают при изменении скорости потока по величине и (или) направлению (в местах сужений, расширений и поворотов трубопроводов; в каналах, вентилях, задвижках, сварных швах и т. д.). Таким образом, потери напора в общем случае находятся как оумма двух величин:

h_п = h_дл + h_мс. (3.36)

Расчету потерь h_дл и h_мс. при ламинарном и турбулентном режимах движения жидкости посвящены разд. 3.11; 3.14; 3.15.

3.11. Профиль скорости в живом сечении и потери напора по длине круглого трубопровода при ламинарном режиме движения жидкости

В круглом трубопроводе (рис. 3.20) выберем поперечное сечение радиусом r и установим для него напряжение трения. С одной стороны, по закону внутреннего трения Ньютона (1.8) а с другой, по основному уравнению равномерного движения (3.33) , так как . Приравнивая правые части этих формул, имеем

.

Отсюда

.

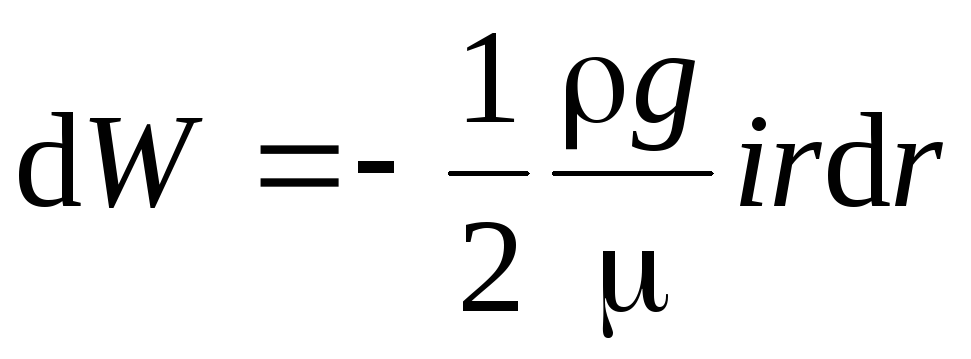Интегрирование дает

Постоянную интегрирования находим из условия: при r = r₀ (на стенке) скорость W = 0. Тогда имеем

или

Поэтому профиль скорости примет вид

(3.37)

Зависимость (3.37) является уравнением параболы. Значит, профиль скорости в живом сечении трубопровода является параболическим (см.рис. 3.20). Из (3.37) видно, что максимальное значение скорости имеет место при r = 0 (на оси трубы): Если это выражение подставить в (3.37), то получим закон Стокса

. (3.38)

Для построения эпюры касательных напряжений снова обратимся к основному уравнению равномерного движения. Из него видно, что величина τ изменяется в зависимости от r_г по линейному закону, причем τ = τ_max при r = r₀, т. е. максимальное касательное напряжение будет на стенке. В соответствии с этим на рис. 3.20 показана эпюра касательных напряжений в жидкости.

Определим расход жидкости по трубе, считая известным поле скорости в живом сечении. Для этого выберем элементарное кольцевое сечение толщиной dr (cм. рис. 3.20), имеющего радиус r. Элементарный объемный расход равен

.

Интегрирование дает

,

или

, (3.39)

где d – диаметр трубы.

Зависимость (3.39) называется уравнением Пуазейля. Определим среднюю скорость потока, пользуясь законом сплошности потока:

, (3.40)

т. е. W_cp = 0,5W_max (см. рис. 3.20), и тогда (3.38) можно записать

. (3.41)

Теперь найдем потери напора по длине трубопровода, пользуясь зависимостью (3.40):

, где l – длина трубопровода.

Отсюда

. (3.42)

Из уравнения (3.42) следует, что при ламинарном режиме движения потери по длине пропорциональны средней скорости в первой степени: . Преобразуем выражение (3.42). Для этого домножим числитель и знаменатель правой части на 2W_cp (индекс "ср" для простоты опустим). Получим

, или , (3.43)

где Re = – критерий Рейнольдса.

Из (3.43) следует, что потери напора по длине выражаются через скоростной напор. Величину, показывающую, во сколько раз напор, затраченный на преодоление трения, отличается от скоростного напора, называют коэффициентом сопротивления по длине

, (3.44)

а отношение 64/Re, входящее в зависимость (3.44), называют коэффициентом гидравлического трения

. (3.45)

Из формул (3.44) и (3.45) видно, что

. (3.46)

В заключение отметим, что результаты расчетов по (3.43) хорошо согласуются с опытными данными.