3.3. Уравнения движения идеальной жидкости (уравнения Эйлера)

Какая зависимость существует между составляющими скоростей и давлений при трехмерном движении идеальной жидкости? Прежде чем искать ответ на вопрос, нужно уяснить, какие силы действуют в движущейся идеальной жидкости. Очевидно, что это – силы инерции, силы давления и сила тяжести. Рассмотрим установившийся поток идеальной жидкости. Выделим в нем элементарный параллелепипед объемом (рис. 2.4). Как было показано при выводе дифференциальных уравнений равновесия Эйлера, проекции на оси координат сил тяжести и сил давления составляют: для оси х: ; для оси у: ; для оси z: . Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение. Масса параллелепипеда равна . Если жидкость движется со скоростью W, то ее ускорение равно , а проеции ускорения на координатные оси равны , и , где , , – составляющие скоростей вдоль осей х, у, z. При этом производные , и отвечают изменению значений , , только во времени (наблюдатель связан с движущейся частицей потока). В соответствии с основным принципом динамики

;

;

,

или

;

;

. (3.10)

Система уравнений (3.10) называется дифференциальными уравнениями движения Эйлера для установившегося потока идеальной жидкости. Производные в левой части (3.10) называются субстанциональными; для установившегося движения они равны

;

;

.

При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке, поэтому при неустановившемся движении в правую часть субстанциональных производных , и дополнительно вводят члены соответственно , и .

3.4. Уравнения движения вязкой жидкости (уравнения Навье-Стокса)

Установим уравнения, описывающие движение вязкий (реальной) капельной жидкости. При движении такой жидкости в ней, помимо сил давления, тяжести и инерции, действуют также силы трения. Выделим в потоке вязкой жидкости элементарный параллелепипед со сторонами dx, dу, d z (рис 3.5).

Сначала рассмотрим случай одномерного плоского потока жидкости в направлении оси х. В этих условиях касательные напряжения возникают лишь на верхней и нижней гранях элементарного параллелепипеда. Если на нижней грани касательное напряжение равно τ, то на верхней равно , где производная выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а – есть изменение этого напряжения вдоль всей длины dz ребра параллелепипеда. Направления сил трения на рис. 3.5 обусловлены тем, что, например, вышележащие над параллелепипедом слои затормаживают его, а слои, лежащие под ним, разгоняют параллелепипед. Проекция равнодействующей сил трения на ось х равна

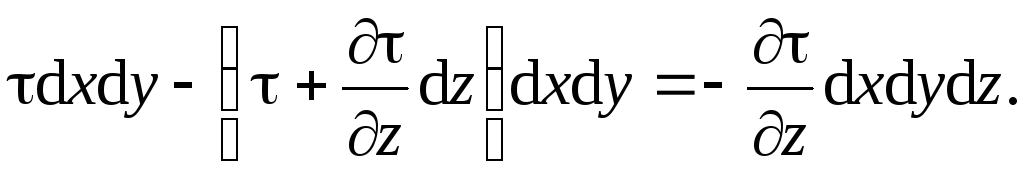
Подставим в это выражение значение касательного напряжения τ по закону Ньютона внутреннего трения (1.8) . Тогда получим

При трехмерном движении жидкости составляющая скорости W_х будет изменяться не только в направлении z, но и в направлении осей координат x и y. Тогда проекция равнодействующей сил трения на ось х примет вид

.

Сумму вторых производных по осям координат называют оператором Лапласа и обозначают

.

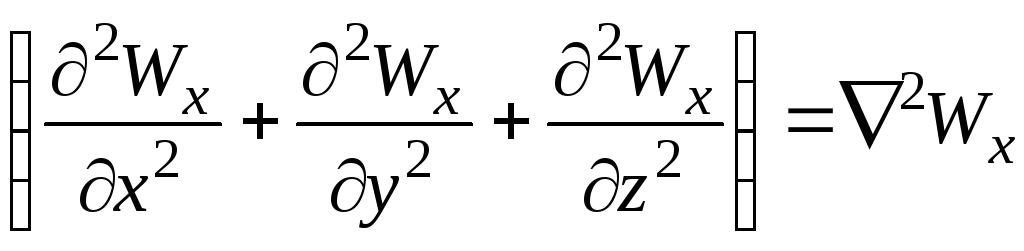Тогда проекция равнодействующей сил трения на ось х запишется По аналогии, проекция равнодействующей сил трения на ось у равна на ось z – Тогда сумма проекций на оси координат давления, тяжести и трения, действующих на элементарный объем, равна: на ось х: ; на ось у: ; на ось z: . В соответствии с основным принципом динамики данные суммы проекций сил равны произведению массы жидкости на проекции ускорения на соответствующие координатные оси. Масса объема составляет Подставляя это выражение в предыдущие формулы и сокращая на dxdydz, получим

;

;

. (3.11)

Уравнения (3.11) называются уравнениями движения Навье-Стокса. В левой части этих уравнений содержится субстанциональная производная, расшифровка которой дана в предыдущем napаграфе. Для идеальной жидкости динамический коэффициент вязкости , и тогда уравнения (3.11) совпадают с уравнениями Эйлера (3.10). Исчерпывающее описание движения вязкой жидкости возможно путем решения уравнений Навье-Стокса (3.11) совместно с уравнением сплошности потока (3.6). Однако современными средствами математики уравнения Навье-Стокса неразрешимы в самом общем виде (уравнения (3.11) – в частных производных, нелинейные, второго порядка), поэтому пока удалось получить точное решение данных уравнений только для простейших случаев движения. В большинстве случаев, при невозможности точного решения уравнений Навье-Стокса, делают упрощающие допущения или преобразуют указанные уравнения методами теории подобия с последующим экспериментированием, что позволяет получать расчетные зависимости полуэмпирического характера.