3.2. Уравнение сплошности (неразрывности) потока

Установим общую зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности (неразрывности) движения, т. е. не образуется пустот, не заполненных жидкостью. Выделим внутри потока элементарный параллелепипед объемом dV = dxdydz, ребра которого ориентированы параллельно осям координат (рис. 3.3). Пусть составляющая скорости потока вдоль оси х в точках, лежащих на левой грани параллелепипеда площадью . равна . Тогда через эту грань в параллелепипед войдет вдоль оси х за единицу времени масса жидкости , а за промежуток времени dτ – масса жидкости , где – плотность жидкости на левой грани параллелепипеда. На противоположной (правой) грани скорость и плотность могут отличаться от соответствующих величин левой грани и будут равны

и .

Рис. 3.3.

Тогда через правую грань из параллелепипеда за тот же интервал времени dτ выйдет масса жидкости

.

Приращение массы жидкости в параллелепипеде вдоль оси х составит

.

Если составляющие скоростей вдоль осей у и z равны и соответственно, то приращения массы в элементарном объеме вдоль этих осей, по аналогии, составят

;

.

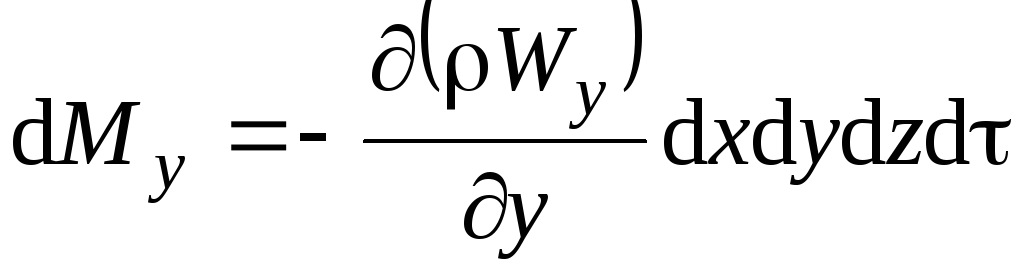Общее накопление массы в параллелепипеде за время dτ равно сумме его приращений вдоль всех осей координат

.

Вместе с тем изменение массы в полностью заполненном жидкостью объеме параллелепипеда возможно только вследствие изменения плотности жидкости в этом объеме. Поэтому . Приравниваем оба выражения и производим сокращение на ; получаем

. (3.4)

Уравнение (3.4) представляет собой дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости. В установившемся потоке плотность не изменяется во времени , и для такого потока уравнение упрощается

. (3.5)

Для капельных жидкостей, которые практически несжимаемы, ρ = const, поэтому из (3.5) следует

. (3.6)

Уравнение (3.6) является дифференциальным уравнением неразрывности потока несжимаемой жидкости. Сумма изменений скорости вдоль осей координат в левой части (3.6) называется дивергенцией вектора скорости и обозначается через . Поэтому (3.6) можно записать так

(3.7)

Проинтегрируем дифференциальное уравнение неразрывности (3.5) для трубопровода переменного сечения, изображенного на рис. 3.4.

Интегрирование дает где S – площадь поперечного сечения трубопровода, W – средняя скорость течения. Тогда для рис. 3.4 имеем

, кг/с, (3.8)

где G – массовый расход жидкости.

Выражение (3.8) – уравнение неразрывности (сплошности) потока в интегральной форме; оно называется также уравнением постоянства расхода: при установившемся движении жидкости, полностью заполняющей трубопровод, через его поперечное сечение проходит за единицу времени одна и та же масса жидкости. Если , тогда из (3.8) имеем

, м³/с, (3.9)

где Q – объемный расход жидкости.

Из (3.9) видно, что скорости жидкости обратно пропорциональны площадям поперечных сечений трубопровода. Массовый и объемный расходы взаимосвязаны: G·= Q ρ.