Лекция 6. Принятие решений с помощью статистической проверки гипотез

6.1. Статистические решения

Основной задачей теории статистических решений является выработка правил поведения в условиях неопределенности, т. е. в условиях, когда человек или техническое устройство, выбирающие тот или иной образ действий, не располагают полной информацией о всех факторах, учет которых оказывает существенное влияние на этот выбор.

Задачи такого рода встречаются, например, при обнаружении слабых сигналов в шумах, при распознавании изображений, при решении вопросов планирования производства, в диагностике, при оценке результатов экспериментальных исследований и т.д.

Теория статистических решений тесно связана с математической статистикой и теорией игр. Математическую статистику часто определяют как науку принятия разумных решений перед лицом неопределенности. С помощью статистических методов можно проанализировать часто возникающие в повседневной жизни ситуации, в которых не вполне очевидно, как следует поступать в том или ином конкретном случае. Раздел теории игр – игры против природы (см. лекц. 24) – относится теории статистических решений, так как в этом случае одному из партнеров игры противостоит некоторая не полностью известная ему обстановка – «состояние природы»

Неопределенность. Существуют два рода неопределенности. Неопределенность первого рода обусловлена случайностью (на результаты наблюдений влияют ошибки измерения, случайный выбор объектов наблюдений, влияние неучтенных вариаций воздействующих факторов). Этот вид неопределенности поддается учету. Он основан на знании законов случайных событий, проявляющихся в каждом случае.

Другой тип неопределенности возникает, когда неизвестно, какой из законов случайных событий действует в конкретном случае. В математической статистике и теории игр принято называть совокупность причин, управляющих ходом случайных событий, состоянием природы.

Информация, необходимая для принятия решения. Процесс принятия статистических решений основывается на результатах статистического вывода.

Информация, необходимая для выполнения статистического вывода, представляется двумя совокупностями объектов:

реально наблюдаемая, статистически представленная рядом из п наблюдений в виде последовательности чисел x1 , x2 , …, xn (т.е. выборка);

теоретически домысливаемая (так называемая генеральная совокупность).

Основные свойства и характеристики выборки, называемые эмпирическими (или выборочными), могут быть проанализированы и вычислены по имеющимся данным. Основные свойства и характеристики генеральной совокупности, называемые теоретическими, не известны исследователю. Получить знания об этих теоретических свойствах и характеристиках можно по соответствующим свойствам и характеристикам выборок в процессе индуктивных рассуждений.

6.2. Основные задачи статистических решений

Различаются два основных вида задач статистических решений: оценивание и проверка гипотез.

Оценивание параметров. С оценкой параметров мы обычно имеем дело, когда нас интересует задача определения неизвестного состояния природы. На основании имеющихся статистических данных необходимо вычислить как можно более точные приближенные значения (статистические оценки) для одного или нескольких параметров, характеризующих функционирование некоторой реальной системы. Очевидно, что

32

максимальный эффект действия, основанного на результатах оценки, будет достигнут, если принятая оценка соответствует истинной величине оцениваемого параметра.

Статистическая оценка. Любая функция от результатов наблюдений исследуемой

случайной величины называется статистикой. Статистика θˆ , используемая в качестве приближенного значения неизвестного параметра θ, называется статистической оценкой. Все статистики и статистические оценки являются случайными величинами. При повторении выборки из той же самой генеральной совокупности и подстановке новых выборочных значений в ту же самую «функцию–оценку» мы получаем другое число в качестве оценки интересующего нас параметра, т.е. имеется неконтролируемый разброс в значениях оценки при повторениях эксперимента. Оценки должны обладать желательными для нас свойствами: эффективности, несмещенности и состоятельности [16].

Проверка гипотез. С проверкой гипотез мы имеем дело тогда, когда среди гипотез, являющихся возможными ответами на данную проблему, заранее выделяется некоторая гипотеза. Эта гипотеза носит название нулевой (Н0). В процессе проверки (тестирования) гипотезы мы должны принять решение об отклонении или принятии этой гипотезы. Причины для выдвижения гипотезы Н0 могут быть различными, но всякий раз требуется, чтобы для Н0 была вычислена вероятность ошибочного решения (вероятность ошибки первого рода).

Задачу проверки гипотез можно определить как задачу, в которой необходимо выбрать одно действие (один вариант) из двух возможных (а1 и а2). Простейшими задачами на проверку гипотез являются такие задачи, в которых рассматриваются только два возможных состояния природы – ψ1 и ψ2.

Предположим, что мы решаем задачу с двумя возможными действиями, причем действие а1 является оптимальным для любого ψ из N1, действие а2 является оптимальным для любого ψ из N2. Само ψ является элементом одного из двух непересекающихся множеств N1 или N2. Рассмотрим гипотезу Н1: ψ N1 и гипотезу Н2: ψ N2.

Чистую стратегию (проверку) можно представить множеством А1 возможных исходов, приводящих к действию а1 (это называется принять Н1, так как выбор действия а1 означает

принятие гипотезы Н1). Проверку можно также представить множеством А2 = A1 возможных исходов, приводящих к а2 (это называется отклонить Н1 или принять Н2).

6.3. Статистическая проверка гипотез

Понятие статистической гипотезы. Гипотеза – это предположительное утверждение, которое может быть или не быть истинным. Будем в дальнейшем обозначать гипотезу буквой Н.

Статистическая гипотеза – это гипотеза, которая допускает наблюдения статистической природы. Можно сказать, что статистическая гипотеза – это

утверждение относительно характера или неизвестных параметров распределения случайных величин. Гипотеза называется простой, если она полностью определяет распределение случайной величины. Например, значение некоторого параметра Θ в точности равно заданной величине Θ0. В других случаях гипотеза называется сложной.

Процедура проверки гипотезы. Из-за невозможности определить истинность гипотезы прямым путем, мы "проверяем" гипотезу, т.е. устанавливаем, не противоречит ли высказанная нами гипотеза имеющимся выборочным данным. Целью проверки гипотезы является оценка правомочности статистической гипотезы. Процедура обоснованного

сопоставления высказанного предположительного утверждения (гипотезы) с результатами наблюдения носит название статистической проверки гипотезы [16].

Результат сопоставления высказанной гипотезы с выборочным данными может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе, а поэтому гипотезу надо отклонить), либо неотрицательным (данные наблюдения не противоречат

33

высказанной гипотезе, а поэтому ее можно принять в качестве одного из возможных решений). При этом неотрицательный результат статистической проверки гипотезы не означает, что высказанное предположительное утверждение является наилучшим: просто гипотеза не противоречит имеющимся выборочным данным, однако таким же свойством наряду с Н могут обладать и другие гипотезы.

Для того чтобы применить вероятностно–статистические принципы к задаче проверки гипотез, необходимо, чтобы гипотеза была сформулирована в виде утверждений, имеющих отношение к характеристикам вероятностного пространства, а именно относительно природы рассматриваемого случайного процесса или величины неизвестных параметров.

Пусть проверяется гипотеза H 0 , при справедливости которой случайная величина (или наблюдение) X имеет плотность f (x; θ0 ) . В качестве альтернативы предлагается гипотеза H1 , при справедливости которой это же наблюдение имеет плотность f (x; θ1) ,

θ0 ≠ θ1 . На практике проверка гипотезы начинается с получения подлежащей анализу

случайной выборки из процесса или генеральной совокупности. По наблюденным значениям случайной величины X (исходам) необходимо сделать вывод об одном из вероятностных распределений, которое могло бы охарактеризовать поведение выборки:

подчиняется ли она закону f (x; θ0 ) или f (x; θ1) .

Область принятия и отклонения гипотезы. Решение об отклонении или принятии гипотезы H0 выносится с помощью правила или процедуры, которая делит диапазон возможных значений исходов в выборке на два множества. Первое из них – это множество принятия гипотезыH0 (область принятия). Второе множество называется множеством отклонения нулевой гипотезы (областью отклонения) или критическим множеством

соответственно множества принятия и отклонения гипотезы. Тогда Ca = Cr , Ca ∩Cr = .

Стандартная процедура проверки нулевой гипотезы состоит в том, что мы наблюдаем реализацию х некоторой случайной величины X и смотрим, какому множеству принадлежит значение х: множеству принятия нулевой гипотезы или критическому множеству. В первом

случае принимается H0 , во втором случае −H1 . Эта процедура выполняется с помощью

статистического критерия, который позволяет сделать выбор между нулевой и альтернативной гипотезами.

Множество принятия нулевой гипотезы и критическое множество) выбираются на основании следующих принципов.

Зададим малую вероятность α совершить ошибку первого рода, т.е. отвергнутьH1 ,

когда она верна. Численное значение α называется уровнем значимости критерия. Обычно значение α выбирают из интервала 0 < α ≤ 0,1. Особенно распространенной является величина уровня значимости 0,05. Зададим также малую вероятность β совершить ошибку

второго рода, т.е. принять H0 , когда она неверна. Вероятность дополнительного события,

т.е. правильного отклонения нулевой гипотезы, называется мощностью критерия. Критическое множество строится на основании принципа отношения правдоподобия

[16,23], его граница определяется, исходя из распределения статистики критерия (см. подразд. 6.5).

Виды альтернативных гипотез. С понятием области принятия или отклонения гипотезы тесно связаны виды альтернативных гипотез (альтернатив). В статистической

34

проверке гипотез рассматриваются три вида альтернатив: двусторонняя, правосторонняя,

левосторонняя альтернативные гипотезы.

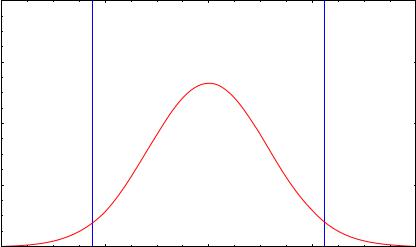
Утверждение, представляющее собой двустороннюю альтернативу, записывается математически с использованием отношения ≠ («не равно»). В этом случае вся область возможных значений статистики критерия разделяется на три части: 1 – область неправдоподобно малых значений, соответствующих Н1, 2 – область значений, соответствующих справедливости Н0, 3 – неправдоподобно больших значений, соответствующих Н1. В этом случае критическая область находится по обе стороны от области принятия (рис.6.1).

Функция плотности вероятности y=нормальное распределение(x;0;1)

0,60

0,45

0,30

0,15

0,00

Рис.6.1. Область принятия нулевой гипотезы Н0 при двусторонней альтернативе (α – уровень значимости)

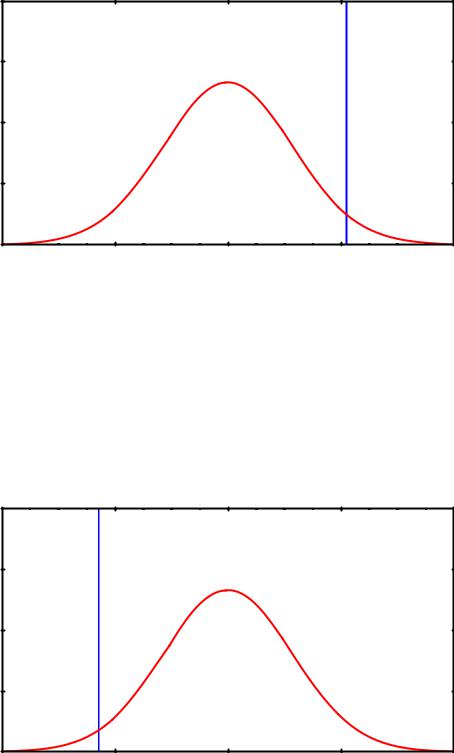
Утверждение, представляющее собой правостороннюю альтернативу, записывается математически с использованием отношения > («больше»). В этом случае вся область возможных значений статистики критерия разделяется на две части: 1 – область значений, соответствующих справедливости Н0, 2 – область значений, соответствующих Н1. В этом случае критическая область находится справа от области принятия (рис. 6.2).

35

Функция плотности вероятности y =нормальное распределение(x;0;1)

0,60

0,45

0,30

0,15

0,00

(1– α)

Рис.6.2. Область принятия нулевой гипотезы Н0 при правосторонней альтернативе (α – уровень значимости)

Утверждение, представляющее собой левостороннюю альтернативу, записывается математически с использованием отношения < («меньше»). В этом случае вся область возможных значений статистики критерия разделяется на две части: 1 – область значений, соответствующих Н1, 2 –область значений, соответствующих справедливости Н0. В этом случае критическая область находится слева от области принятия (рис. 6.3).

Функция плотности вероятности y=нормальное распределение(x;0;1)

0,60

0,45

0,30

0,15

0,00

(α)

Рис.6.3. Область принятия нулевой гипотезы Н0 при правосторонней альтернативе (α – уровень значимости)

36