
- •1.1. Методы искусственного интеллекта в прикладных системах и системах принятии решений
- •1.2. Интеллектуальные информационные технологии в прикладных системах и системах принятия решений
- •1.3. Типология задач интеллектуализации систем
- •Лекция 2. Представление знаний в интеллектуальных системах
- •2.1. Модели представления знаний
- •2.2. Системы, основанные на правилах
- •2.3. Системы, основанные на автоматическом доказательстве теорем
- •2.4. Системы, основанные на автоматическом порождении (выдвижении) гипотез
- •Лекция 3. Структура и основные компоненты прикладных интеллектуальных систем
- •3.1. Прикладные системы, основанные на знаниях
- •3.2. Структура системы управления, основанной на знаниях
- •3.3. Структура интеллектуальных систем поддержки принятия решения
- •3.4. Обобщенная структура экспертной системы
- •Лекция 4. Классификация прикладных интеллектуальных систем
- •4.1. Классификация экспертных систем
- •4.2. Примеры прикладных интеллектуальных систем
- •Лекция 5. Основные понятия и определения теории принятия решений
- •5.1. Роли людей в процессе принятия решений
- •5.2. Альтернативы
- •5.3. Критерии
- •5.4. Основные этапы процесса принятия решений
- •5.5. Математические методы теории принятия решений
- •Лекция 6. Принятие решений с помощью статистической проверки гипотез
- •6.1. Статистические решения
- •6.2. Основные задачи статистических решений
- •6.3. Статистическая проверка гипотез
- •6.4. Ошибки решения
- •6.5. Решающее правило при проверке гипотез
- •Лекция 7. Байесовская и последовательная процедуры принятия решения.
- •7.1. Байесовские процедуры принятия решения
- •7.1.1. Байесовская процедура при проверке простой гипотезы
- •7.1.2. Байесовские процедуры в задаче классификации
- •7.2. Принятие решения с помощью последовательной процедуры Вальда
- •Лекция 8. Принятие решения методом дискриминантнного анализа
- •8.1. Классификация в случае, когда распределения классов определены полностью
- •8.1.1. Модель двух нормальных распределений с общей ковариационной матрицей (модель Фишера)
- •8.1.2. Модель двух нормальных распределений с разными ковариационными матрицами
- •8.1.3. Модель нескольких нормальных распределений с общей ковариационной матрицей
- •8.2. Классификация при наличии обучающих выборок
- •8.2.1. Подстановочный алгоритм в модели Фишера
- •8.2.3. Правила классификации
- •8.3. Ошибка решающего правила
- •Лекция 9. Древообразные классификаторы
- •9.1. Назначение древообразных классификаторов
- •9.1. Структура дерева классификации
- •9.3. Вычислительные задачи древообразных классификаторов
- •9.3.1. Определение качества предсказания
- •9.3.2. Выбор разбиений
- •9.3.3. Определение правила прекращения разбиения
- •Лекция 10. Деревья решений
- •9.1. Характеристики дерева решений
- •9.2. Построение дерева решений
- •Лекция 11. Методы прогнозирования
- •11.1. Анализ временных рядов
- •11.1.1. Модель временного ряда
- •11.1.2. Тренд, сезонная и циклическая компоненты
- •11.1.3. Декомпозиция временного ряда
- •11.1.4. Экспоненциальное сглаживание
- •11.2. Каузальные методы прогнозирования
- •11.3. Качественные методы прогнозирования
- •Лекция 12. Основная задача линейного программирования
- •12.1. Математическая модель основной задачи линейного программирования
- •12.2. Задача линейного программирования с ограничениями-неравенствами
- •12.3. Примеры задач линейного программирования
- •12.3.1. Транспортная задача
- •12.3.2. Задача о назначениях
- •Лекция 13. Симплекс-метода решения задачи линейного программирования
- •13.1. Характеристика симплекс–метода
- •13.2. Табличный алгоритм замены базисных переменных
- •13.3. Отыскание опорного решения основной задачи линейного программирования
- •13.4. Отыскание оптимального решения основной задачи линейного программирования
- •Лекция 14. Многокритериальные методы принятия решений при объективных моделях
- •14.1. Объединение критериев
- •14.2. Метод главного критерия
- •14.3. Метод последовательных уступок
- •14.4. Метод целевого программирования
- •14.5. Метод, использующий принцип гарантированного результата
- •14.6. Метод равных наименьших относительных отклонений
- •14.7. Процедура STEM поиска удовлетворительных значений критериев
- •Лекция 15. Выбор Парето–оптимальных решений
- •15.1. Основные определения
- •15.2. Графическая интерпретация
- •15.3. Постановка задачи
- •Лекция 16. Оценка многокритериальных альтернатив с помощью теории полезности
- •16.1. Теория полезности
- •16.2. Принятие решения на основе значения ожидаемой полезности
- •16.3. Многокритериальная теория полезности (MAUT)
- •Лекция 17. Сравнение альтернатив методом аналитической иерархии
- •17.1. Основные этапы метода аналитической иерархии
- •17.2. Декомпозиция задачи
- •17.3. Попарное сравнение критериев и альтернатив
- •17.4. Свойства идеальной матрицы сравнений
- •Лекция 18. Приоритеты для критериев и альтернатив и выбор наилучшей альтернативы в методе анализа иерархий
- •18.1. Вычисление собственных характеристик обратно симметричной матрицы
- •18.2. Вычисление величины приоритетов
- •18.3. Определение наилучшей альтернативы
- •18.4. Проверка согласованности
- •18.5. Пример применения метода анализа иерархий
- •Лекция 19. Оценка многокритериальных альтернатив методами ELECTRE
- •19.1. Этапы подхода, направленного на разработку индексов попарного сравнения альтернатив
- •19.2. Свойства бинарных отношений
- •19.3. Метод ELECTRE I
- •19.4. Метод ELECTRE II
- •19.5. Метод ELECTRE III
- •Лекция 20. Основные понятия и математическая модель игровых методов обоснования решений
- •20.1. Основные понятия теории игр
- •20.2. Математическая модель игры
- •20.3. Нижняя и верхняя цена игры. Принцип минимакса
- •Лекция 21. Методы решения игр
- •21.1. Решение игры в чистых стратегиях
- •21.2. Решение игры в смешанных стратегиях
- •21.3. Упрощение игр
- •21.4. Решение игры 2х2
- •21.5. Графический метод решения (2х2)-игр
- •Лекция 22. Игры 2 х п
- •Лекция 23. Решение игр т х 2 и т х п
- •23.1. Решение игр т х 2
- •23.2. Решение игр т х п
- •Лекция 24. Критерии принятия решений в условиях риска и неопределенности
- •24.1. Основные понятия. Математическая модель
- •24.3. Максиминный критерий Вальда
- •24.4. Критерий минимаксного риска Сэвиджа
- •24.5. Критерий пессимизма-оптимизма Гурвица
- •Литература
w |
|
|
0 |
1 |
p |
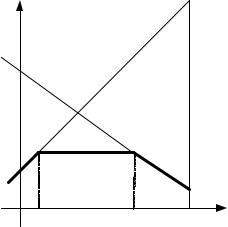
Рис. 22.6. Нижняя огибающая с горизонтальным участком
Найдем теперь полное решение игры из примера 22.1, т.е. определим оптимальную смешанную стратегию Q0 = { q10 , q20 , q30 , q40 , q50 , q60 } игрока В.
Выделяем из шести чистых стратегий игрока В стратегии В4 и В5, которые соответствуют прямым (4) и (5), определяющим наивысшую точку нижней огибающей. Для этого полагаем
q10 = 0, q20 = 0, q30 = 0, q40 = q, q50 = 1 – q, q60 = 0.
Далее приравняем любой из двух средних выигрышей игрока В (игрок А выбирает только чистые стратегии), отвечающие предложенной смешанной стратегии
0 |
0 |
0 |
q 1 – q 0 |
||
6 |
4 |
3 |
1 |
–1 |
0 |
–2 |
–1 |
1 |
0 |
5 |
4 |
к цене игры:
q – (1 – q) = 5/7, 5 (1 – q) = 5/7.
Получаем, что q0 = 6/7.
Полное решение игры имеет следующий вид:
Р0 = {5/7, 2/7}, Q0 = {0, 0, 0, 6/7, 1/7, 0}, v = 5/7.
Лекция 23. Решение игр т х 2 и т х п
23.1. Решение игр т х 2
Пусть в матричной игре две чистые стратегии имеет игрок В, а число чистых стратегий игрока А произвольно (т).
В этом случае платежная матрица игры имеет вид
a |
a |
|
|
a11 |
a12 |
|
|
|
21 |
22 |
. |
|
.......... |
|
|
aт1 aт2 |
|
||
Проанализируем . т х 2-игру.
108
Пусть Q = {q, 1 – q} – произвольная смешанная стратегия игрока В. Если игрок А выбрал i-ю чистую стратегию, i = 1, 2,…,m, то средний выигрыш игрока В в ситуации {Q, i } оказывается равным
(i) : w = ai1q + ai2 (1 – q), i = 1, 2,…, m. |
(23.1) |
Зависимость этого выигрыша от переменной q описывается прямой. Графиком функции
max ( ai1q + ai2 (1 – q))
1≤i≤m
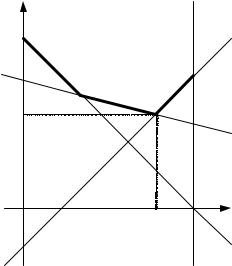
является верхняя огибающая семейства прямых (23.1), соответствующих чистым стратегиям игрока А (рис. 23.1).
w |
|
|
|
w0 |
|
|
|
0 |
q0 |
1 |
q |
Рис. 23.1. Верхняя огибающая семейства прямых, оптимальная смешанная стратегия q0 и цена игры w0 игрока В
Отыскание оптимальной смешанной стратегии игрока А проводится по той же схеме, которая обеспечивает нахождение оптимальной смешанной стратегии игрока В в игре 2 х п.
Пример 23.1 [28]. Рассмотрим игру, заданную 3 х 2-матрицей
|
3 −1 |
|
|
|
−1 |
3 |
. |
|
1 |
0 |
|
|
|
||
Решение.
1-й шаг. Анализ игры на наличие седловой точки.
Нижняя цена игры равна 0, верхняя – равна 3. Седловая точка отсутствует. Решение нужно искать в смешанных стратегиях.
2-й шаг. Вычисление средних выигрышей игрока В. При этом предполагается, что игрок
А выбирает только чистые стратегии. Из таблицы
q |
1 – q |
3 |
–1 |
–1 |
3 |
1 |
0 |
Получаем
(7): w = 3q – (1 – q),
(8): w = –q + 3 (1 – q),
(9): w = q.
3-й шаг. Построение нижней огибающей.
109
Строим на координатной плоскости (q, w) все три прямые, уравнения которых были получены на втором шаге, и находим их верхнюю огибающую.
4-й шаг. Отыскание цены игры и оптимальной смешанной стратегии игрока В.
Нижняя точка верхней огибающей является точкой пересечении прямых (1) и (2).. Решая систему уравнений
w = |
3q – (1 – q), |
w = |
–q + 3 (1 – q), |
получаем |
|
q 0 = 1/2, w0 = 1.
5-й шаг. Отыскание оптимальной смешанной стратегии игрока А.
Полагая
р10 = р, р20 = 1 – р, р30 = 0,
приравниваем средние выигрыши игрока А, соответствующие чистым стратегиям игрока В: 3р – (1 – р) = – р + 3(1 – р),
и находим р0 = ½.
Таким образом, цена игры и оптимальные смешанные стратегии игроков А и В соответственно равны:
v = 1, Р0 = {1/2, 1/2}, Q0 = {1/2, 1/2}.
23.2. Решение игр т х п
При больших т и п решение игр т х п становится весьма трудоемким. Решение любой матричной игры может быть сведено к задаче линейного программирования (см. лекц.12).
Рассмотрим т х п-игру, заданную т х п – матрицей А = (аik). Игрок А имеет т
стратегий: А1, А2,…, Ат, а игрок В – п стратегий: В1, В2,…, Вп.
Требуется найти решение игры, т.е. две оптимальные смешанные стратегии игроков А и
В:
Р0 = {р1, р2, …, рт }, Q0 = {q1 , q2, …, qn}.
Найдем оптимальную смешанную стратегию Р0 игрока А. Эта стратегия должна обеспечить игроку А выигрыш, не меньший v, при любом поведении игрока В, и выигрыш, равный v, при его оптимальном поведении, т.е. при стратегии Q0 [5].
Пусть цена игры v > 0. Чтобы выполнялось это условие, достаточно, чтобы все элементы платежной матрицы (аik) были неотрицательными. Если не все аik удовлетворяют условию аik > 0, то матрицу А = (аik) можно преобразовать к матрице A′ = (аik + М),
прибавив ко всем элементам матрицы (аik) одну и ту же большую положительную величину. Решают игру с матрицей A′ , при этом оптимальные стратегии игры не изменятся, а цена игры v увеличится на М: ν′= v + М.
Запишем условия, обеспечивающие средний выигрыш при всех чистых стратегиях игрока В:
р1a11 + р2a21 +...+ pmam1 ≥ ν, |
|
|
|||||||||
р1a12 |
+ р2a22 |
+ + pmam2 |
≥ ν, |
|
(23.2) |
||||||
|
|||||||||||
............................................. |
|
|
|||||||||
р a |
+ р |
2 |
a |
2n |
+...+ p |
m |
a |
mn |
≥ ν. |
|
|
1 1n |
|
|
|
|
|
|
|
||||
Разделим неравенства (23.2) на положительную величину v и введем обозначения:
х1 = |
р1 |
, |
х2 = |
р2 |
, …, хт = |
рт |
, |
(23.3) |
ν |
ν |
|
||||||
|
|
|
|
ν |
|
|||
Тогда условия (23.2) запишутся в виде:
110

a11x1 + a21x2 +...+ aт1xт ≥1, |
|
|||||
a12x1 |
+ a22x2 |
+ + aт2xт ≥1, |
|
|||
|
||||||
............................................. |
|
|||||
a x |
+ a |
x |
+...+ a |
x |
≥1, |
|
1п 1 |
|
2п 2 |
|
mn |
n |
|
где х1, х2 ,…, хт – неотрицательные переменные. В силу (23.3) и того, что
(23.4)
m
∑pi = 1, эти i=1
переменные удовлетворяют условию
х1+ х2 +… + хт = 1/v. (23.5)
Гарантированный выигрыш должен быть максимально возможным. При этом правая часть (23.5) принимает минимальное значение. Таким образом, задача решения игры свелась к следующей математической задаче.
Определить неотрицательные значения переменных х1, х2 ,…, хт так, |
чтобы они |
удовлетворяли линейным ограничениям (23.4) и при этом их линейная функция |
|
L = х1+ х2 +… + хт |
(23.6) |
обращалась в минимум. |
|
Это формулировка задачи линейного программирования. |
|
Решая задачу линейного программирования, мы можем найти оптимальную смешанную стратегию Р0 игрока А.
Найдем теперь оптимальную стратегию Q0 игрока В. Нахождение решения будет аналогичным решению игры для игрока А. Отличие будет состоять в том, что игрок В стремится не максимизировать, а минимизировать выигрыш, т.е. максимизировать величину 1/v. Вместо условия (23.4) должны будут соблюдаться условия:
a11y1 + a12 y2 +... + a1n yn ≤1, |
|
||||||||||
a21y1 |
+ a22 y2 |
+ + a2n yn ≤1, |
|
||||||||
|
|||||||||||
............................................. |
|
||||||||||
a |
y |
+ a |
п2 |
y |
2 |
+...+ a |
nn |
y |
n |
≤1, |
|
|
п1 1 |
|
|
|
|
|
|
||||
где у1, у2 ,…, уп – неотрицательные переменные, равные
у1 = qν1 , у2 = qν2 , …, уп = qνn .
Требуется определить неотрицательные значения переменных у1, у2 ,…, уп они удовлетворяли линейным ограничениям (23.7) и обращали в максимум функцию
(23.7)
(23.8)
так, чтобы линейную
L = у1+ у2 +…+ уп = 1/v . |
(23.9) |
Вместо того, чтобы максимизировать функцию (23.9), можно минимизировать функцию
L′ = – L = –у1 – у2 –…– уп = –1/v.
Таким образом, мы свели задачу решения любой конечной игры к задаче линейного программирования. Методы решения таких задач изложены в лекц. 12 и 13.
Сведение к задаче линейного программирования не всегда оказывается самым простым способом. Наиболее часто используются следующие способы упрощения игры:
1)уменьшение размеров платежной матрицы игры; число стратегий сокращается путем вычеркивания излишних стратегий (см. лекц. 21);
2)для игр с небольшими т и п необходимо установить, какие стратегии являются активными. После этого игра сводится к игре с меньшей размерностью. Например, для квадратной матрицы (т = п) можно установить, не является ли игра полностью усредненной.
Вэтом случае все стратегии обеих сторон являются активными, а неравенства (23.4)
обращаются в равенства. Решив эту систему уравнений, получим положительные значения х1, х2 ,…, хт. Складывая их, найдем величину 1/v:
х1+ х2 +… + хт = 1/v,
откуда цена игры
111
v= 1/(х1+ х2 +… + хт),
авероятности р1, р2, …, рт в оптимальной стратегии Р0 найдутся как
р1 = х1v, р2 = х12,…, рт = хтv.
Пример 23.2 [26]. Решить игру, заданную 3 х 2-матрицей
3 812 1 ,
9 6
сведя ее к задаче линейного программирования.
Решение.
1. Анализируем игру на наличие седловой точки.
Нижняя цена игры равна 6, верхняя – равна 8. Седловая точка отсутствует. Решение нужно искать в смешанных стратегиях.
2. По матрице игры составляем задачи (23.4), (23.5) – (23.9):
|
Задача 1 (игрок А) |
Задача 2 (игрок В) |
|
|
|
|
L1 = х1+ х2 + х3 → min, |
L2 = у1+ у2 → max, |
|
|
|
|
3х1+12 х2 + 9 х3 ≥ 1, |
3у1+ 8 у2 ≤ 1, |
|
|
|
|
8х1+ х2 + 6 х3 ≥ 1, |
12у1+ у2 ≤ 1, |
|
|
|
|
хi ≥ 0, i = 1, 2, 3. |
9у1+ 6 у2 ≤ 1, |
|
|
|
|
|
уj ≥ 0, j = 1, 2. |
|
|
|
3. Решаем задачу отыскания оптимальной смешанной стратегии игрока В (задача 2) |
|||||
методом линейного программирования (см. |
лекц. 12): у0 |
=1/4, у0 |
= 1/9, L2max = 4/27. |
||
|
|
1 |
2 |
|
|
Используя формулы (23.8) и (23.9), получаем: v = 27/4, q0 = ¼, q0 = ¾. |
|
|
|||
|
|
1 |
2 |
|
|
4. Для определения оптимальной смешанной стратегии |
Ро = { р10 , р20 , р30 } игрока А |
||||
найдем решение задачи 1 линейного программирования. В оптимальном плане второй задачи у10 > 0 и у20 > 0, поэтому оба ограничения на оптимальном плане хо = { х10 , х20 , х30 } активны.
Кроме того, на у0 второе ограничение выполняется как строгое неравенство, Следовательно, в оптимальном плане первой задачи соответствующая этому ограничению вторая
переменная равна нулю: х20 = 0. Поэтому для определения х10 и х30 получаем систему
уравнений
3х1+12 х2 + 9 х3 ≥ 1, 8х1+ х2 + 6 х3 ≥ 1,
решая которую находим: х10 = 3/54, х30 = 5/54.
Используя (23.8) и (23.9) определяем р10 = 3/8, р20 = 0, р30 = 5/8.
Таким образом, решение игры Ро = {3/8,0 ,5/8}, Q0 = {¼ , ¾}, v = 27/4.
Это означает, что для получения максимального среднего выигрыша v = 27/4 игрок А должен с вероятностью 3/8 использовать свою чистую стратегию А1, с вероятностью 5/8 – чистую стратегию А3. Это активные стратегии. Стратегию А2 использовать не нужно, так как это пассивная стратегия.
Игрок В для обеспечения минимального среднего проигрыша должен с вероятностью 1/4 использовать свою чистую стратегию В1, с вероятностью 3/4 – чистую стратегию В2.
112
