где U(х), Ui (x) – функции полезности, изменяющиеся от 0 до 1; wi – коэффициенты важности (веса) критериев, 0 < wi < 1; коэффициент k > –1. Многокритериальную функцию полезности можно определить, если известны значения коэффициентов wi , k, а также однокритериальные функции полезности Ui (x) .

Лекция 17. Сравнение альтернатив методом аналитической иерархии

17.1. Основные этапы метода аналитической иерархии

Метод анализа иерархий, разработанный Т. Саати [19] является одним из наиболее известных методов выбора наилучшей альтернативы из множества предложенных. В основе метода аналитической иерархии (АИ) лежит идея сравнения заданных альтернатив. Использование данного метода предполагает представление экспертами исследуемой проблемы в виде иерархий критериев и подчиненных им альтернатив.

Постановка задачи, решаемой с помощью метода АИ, заключается в следующем. Заданы общая цель (или цели) решения задачи; т критериев оценки альтернатив; п альтернатив. Требуется выбрать наилучшую альтернативу.

Суть метода анализа иерархий состоит в следующем.

1.Первый этап заключается в декомпозиции задачи в трехуровневую иерархию «цели – критерии – альтернативы».

2.На втором этапе ЛПР выполняет попарные сравнения элементов каждого уровня иерархии. Результаты сравнений переводятся в числа, указывающие степень превосходства одного элемента над другим.

3.Вычисляются коэффициенты важности (величины локальных приоритетов) для критериев и альтернатив. При этом проверяется согласованность суждений ЛПР.

4.Подсчитывается количественный индикатор важности (глобальный приоритет) каждой из альтернатив и определяется наилучшая альтернатива.

17.2.Декомпозиция задачи

Очень часто при анализе интересующей нас структуры число элементов и их взаимосвязей настолько велико, что затрудняет воспринимать информацию в полном объеме. В таких случаях система делится на подсистемы. Одним из таких делений является иерархическое.

Иерархии представляют собой определенный вид системы, основанный на предположении, что ее элементы могут группироваться в не связанные множества. При этом элементы каждой группы находятся под влиянием элементов некоторой другой группы и в свою очередь оказывают влияние на элементы третьей группы.

Первым требованием при анализе функционирования системы является построение иерархии, воспроизводящей функциональные отношения. Для этого сначала перечисляются все элементы, относящиеся к иерархии. Затем они распределяются по группам в соответствии с влиянием между группами. Так возникают уровни иерархии. Определяются цели, ради которых решается задача, и строится иерархия.

Допустим, что при рассмотрении некоторой проблемы, решение которой сводится к выбору из множества альтернатив, группа экспертов пришла к соглашению о декомпозиции этой проблемы в трехуровневую иерархию «цели – критерии – альтернативы», представленную на рис. 17.1.

Пример [12]. Предположим, комиссия по выбору места строительства аэропорта предварительно отобрала из нескольких возможных четыре варианта: А, В, С, D. Тогда структура решаемой задачи может быть представлена в виде, показанном на рис. 17.2.

84

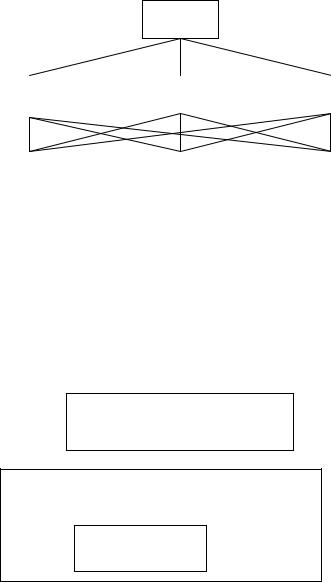
Цель

Рис. 17.1. Декомпозиция решаемой задачи в трехуровневую структуру

17.3. Попарное сравнение критериев и альтернатив

На данном этапе осуществляется формирование матрицы относительной важности критериев по отношению к цели. Элементы данной матрицы (табл. 17.1) представляют собой попарные отношения важности j-го и l-го критериев, которые вырабатываются экспертами и выражаются ими в числовой форме с использованием специальной шкалы относительной важности.

Цель

Цель строительства аэропорта: прием и отправка большого числа пассажиров

Критерии

Время в пути от аэропорта до центра города

Альтернативы

Рис 17.2. Иерархическая схема проблемы выбора места для аэропорта

Таблица 17.1

Матрица попарных сравнений критериев по важности

85

После сравнений критериев формируются матрицы попарных сравнений альтернатив

на предпочтительность по каждому критерию [2, 11, 28]. Элементы этих матриц представляют собой попарные отношения предпочтительности i-й альтернативы над k-й альтернативы для каждого критерия, которые также вырабатываются экспертами и выражаются ими в числовой форме по той же шкале относительной важности.

Таблица сравнений (табл. 17.1) строится по следующим правилам:

если элементы А и В одинаково важны, заносим в клетку (А, В) таблицы сравнений число 1;

если элемент А умеренно превосходит В – число 3; если элемент А существенно важнее В – число 5; если элемент А значительно важнее В – число 7;

если элемент А по своей значимости абсолютно превосходит В – число 9.

Числа 2, 4, 6, 8 используются для облегчения компромиссов между оценками, слегка отличающимися от основных чисел. Рациональные дроби используются в случае, когда желательно увеличить согласованность всей матрицы при малом числе суждений.

17.4. Свойства идеальной матрицы сравнений

Для вычисления локальных приоритетов и проверки согласованности суждений ЛПР необходимо знать ряд свойств идеальной матрицы сравнений [28]. Возьмем отношения

Проанализируем некоторые свойства этой идеальной матрицы сравнений.

значением λ = п. Собственным вектором квадратной матрицы А называется такой ненулевой вектор-столбец, при умножении на который матрицы А получается вектор-столбец, пропорциональный исходному вектору х, т.е. Ах = λх. Число λ называется собственным

86