
- •1.1. Методы искусственного интеллекта в прикладных системах и системах принятии решений
- •1.2. Интеллектуальные информационные технологии в прикладных системах и системах принятия решений
- •1.3. Типология задач интеллектуализации систем
- •Лекция 2. Представление знаний в интеллектуальных системах
- •2.1. Модели представления знаний
- •2.2. Системы, основанные на правилах
- •2.3. Системы, основанные на автоматическом доказательстве теорем
- •2.4. Системы, основанные на автоматическом порождении (выдвижении) гипотез
- •Лекция 3. Структура и основные компоненты прикладных интеллектуальных систем
- •3.1. Прикладные системы, основанные на знаниях
- •3.2. Структура системы управления, основанной на знаниях
- •3.3. Структура интеллектуальных систем поддержки принятия решения
- •3.4. Обобщенная структура экспертной системы
- •Лекция 4. Классификация прикладных интеллектуальных систем
- •4.1. Классификация экспертных систем
- •4.2. Примеры прикладных интеллектуальных систем
- •Лекция 5. Основные понятия и определения теории принятия решений
- •5.1. Роли людей в процессе принятия решений
- •5.2. Альтернативы
- •5.3. Критерии
- •5.4. Основные этапы процесса принятия решений
- •5.5. Математические методы теории принятия решений
- •Лекция 6. Принятие решений с помощью статистической проверки гипотез
- •6.1. Статистические решения
- •6.2. Основные задачи статистических решений
- •6.3. Статистическая проверка гипотез
- •6.4. Ошибки решения
- •6.5. Решающее правило при проверке гипотез
- •Лекция 7. Байесовская и последовательная процедуры принятия решения.
- •7.1. Байесовские процедуры принятия решения
- •7.1.1. Байесовская процедура при проверке простой гипотезы
- •7.1.2. Байесовские процедуры в задаче классификации
- •7.2. Принятие решения с помощью последовательной процедуры Вальда
- •Лекция 8. Принятие решения методом дискриминантнного анализа
- •8.1. Классификация в случае, когда распределения классов определены полностью
- •8.1.1. Модель двух нормальных распределений с общей ковариационной матрицей (модель Фишера)
- •8.1.2. Модель двух нормальных распределений с разными ковариационными матрицами
- •8.1.3. Модель нескольких нормальных распределений с общей ковариационной матрицей
- •8.2. Классификация при наличии обучающих выборок
- •8.2.1. Подстановочный алгоритм в модели Фишера
- •8.2.3. Правила классификации
- •8.3. Ошибка решающего правила
- •Лекция 9. Древообразные классификаторы
- •9.1. Назначение древообразных классификаторов
- •9.1. Структура дерева классификации
- •9.3. Вычислительные задачи древообразных классификаторов
- •9.3.1. Определение качества предсказания
- •9.3.2. Выбор разбиений
- •9.3.3. Определение правила прекращения разбиения
- •Лекция 10. Деревья решений
- •9.1. Характеристики дерева решений
- •9.2. Построение дерева решений
- •Лекция 11. Методы прогнозирования
- •11.1. Анализ временных рядов
- •11.1.1. Модель временного ряда
- •11.1.2. Тренд, сезонная и циклическая компоненты
- •11.1.3. Декомпозиция временного ряда
- •11.1.4. Экспоненциальное сглаживание
- •11.2. Каузальные методы прогнозирования
- •11.3. Качественные методы прогнозирования
- •Лекция 12. Основная задача линейного программирования
- •12.1. Математическая модель основной задачи линейного программирования
- •12.2. Задача линейного программирования с ограничениями-неравенствами
- •12.3. Примеры задач линейного программирования
- •12.3.1. Транспортная задача
- •12.3.2. Задача о назначениях
- •Лекция 13. Симплекс-метода решения задачи линейного программирования
- •13.1. Характеристика симплекс–метода
- •13.2. Табличный алгоритм замены базисных переменных
- •13.3. Отыскание опорного решения основной задачи линейного программирования
- •13.4. Отыскание оптимального решения основной задачи линейного программирования
- •Лекция 14. Многокритериальные методы принятия решений при объективных моделях
- •14.1. Объединение критериев
- •14.2. Метод главного критерия
- •14.3. Метод последовательных уступок
- •14.4. Метод целевого программирования
- •14.5. Метод, использующий принцип гарантированного результата
- •14.6. Метод равных наименьших относительных отклонений
- •14.7. Процедура STEM поиска удовлетворительных значений критериев
- •Лекция 15. Выбор Парето–оптимальных решений
- •15.1. Основные определения
- •15.2. Графическая интерпретация
- •15.3. Постановка задачи
- •Лекция 16. Оценка многокритериальных альтернатив с помощью теории полезности
- •16.1. Теория полезности
- •16.2. Принятие решения на основе значения ожидаемой полезности
- •16.3. Многокритериальная теория полезности (MAUT)
- •Лекция 17. Сравнение альтернатив методом аналитической иерархии
- •17.1. Основные этапы метода аналитической иерархии
- •17.2. Декомпозиция задачи
- •17.3. Попарное сравнение критериев и альтернатив
- •17.4. Свойства идеальной матрицы сравнений
- •Лекция 18. Приоритеты для критериев и альтернатив и выбор наилучшей альтернативы в методе анализа иерархий
- •18.1. Вычисление собственных характеристик обратно симметричной матрицы
- •18.2. Вычисление величины приоритетов
- •18.3. Определение наилучшей альтернативы
- •18.4. Проверка согласованности
- •18.5. Пример применения метода анализа иерархий
- •Лекция 19. Оценка многокритериальных альтернатив методами ELECTRE
- •19.1. Этапы подхода, направленного на разработку индексов попарного сравнения альтернатив
- •19.2. Свойства бинарных отношений
- •19.3. Метод ELECTRE I
- •19.4. Метод ELECTRE II
- •19.5. Метод ELECTRE III
- •Лекция 20. Основные понятия и математическая модель игровых методов обоснования решений
- •20.1. Основные понятия теории игр
- •20.2. Математическая модель игры
- •20.3. Нижняя и верхняя цена игры. Принцип минимакса
- •Лекция 21. Методы решения игр
- •21.1. Решение игры в чистых стратегиях
- •21.2. Решение игры в смешанных стратегиях
- •21.3. Упрощение игр
- •21.4. Решение игры 2х2
- •21.5. Графический метод решения (2х2)-игр
- •Лекция 22. Игры 2 х п
- •Лекция 23. Решение игр т х 2 и т х п
- •23.1. Решение игр т х 2
- •23.2. Решение игр т х п
- •Лекция 24. Критерии принятия решений в условиях риска и неопределенности
- •24.1. Основные понятия. Математическая модель
- •24.3. Максиминный критерий Вальда
- •24.4. Критерий минимаксного риска Сэвиджа
- •24.5. Критерий пессимизма-оптимизма Гурвица
- •Литература
значением матрицы А. Квадратная матрица п-го порядка имеет не более п собственных значений.
В самом деле, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
w |
w |
|
|
w |
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
|
... |
|
1 |
|
|
|
|
|
|
|
|
|
|
w2 |
wn |
|
|
|
|
|
|
|
|
|||||||
w1 |
|
|
|
|
nw |
|
|
w |
|
|||||||
w2 |
w2 |
|
|
w2 |
w |
|
|
|
|
|||||||
|
w1 |
w2 |
... wn |
|
1 |
= |
.... |
1 |
|
|
1 |
= пw. |
||||
Аw = |
|
.... |
|
= п |
.... |
|||||||||||
.................... |
|
wn |
nwn |
|
wn |
|||||||||||
w |
w |
... |
w |
|
|
|
|
|
|
|
|
|
||||
|
n |
n |
n |
|
|
|
|
|
|
|
|
|||||
|
w |
w |
|
|
w |
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|||
Обратно симметричные и согласованные матрицы. Рассмотрим квадратную положительную матрицу А порядка п. Матрица А называется обратно симметричной, если
для любых i и k выполняется соотношение аki = 1/ аik.
Матрица А называется согласованной, если для любых i, k и l имеет место равенство
аik аkl = аil.
Отсюда следует, что матрица сравнений – обратно симметричная и согласованная. Справедливо следующее утверждение.
Теорема. Положительная обратно симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение
совпадают: λmax = п.
Матрицы относительной важности критериев и альтернатив являются обратно симметричными. Их главная диагональ состоит из единиц, так как на ней расположены результаты сравнения одинаковых критериев. Остальные элементы матрицы относительно главной диагонали представляют собой обратные величины.
Лекция 18. Приоритеты для критериев и альтернатив и выбор наилучшей альтернативы в методе анализа иерархий
Матрицы сравнений важности критериев и альтернатив (см. лекц. 17), полученные на втором этапе анализа, позволяют рассчитывать коэффициенты важности, или величины локальных приоритетов. Они показывают относительное влияние множества элементов иерархии на элемент примыкающего к ним верхнего уровня. Для этого нужно вычислить собственное значение и собственный вектор матрицы сравнений.
18.1. Вычисление собственных характеристик обратно симметричной матрицы
Методы вычисления собственных характеристик матриц хорошо известны. Они весьма трудоемки и требуют большого числа вычислений. Существуют приближенные методы, разработанные для обратно симметричных матриц. В них сначала приближенно находится собственный вектор, а затем по нему ищется приближенное собственное значение.
Вычисление собственного вектора. Опишем несколько способов приближенного вычисления собственного вектора [28].
1-й способ:
1)суммируем элементы каждой строки и записываем полученные результаты в
столбец;
2)складываем все элементы найденного столбца;
3)делим каждый элемент на полученную сумму.
2-й способ:
87
1)суммируем элементы каждого столбца и записываем полученные результаты в
столбец;
2)заменяем каждый элемент построенного столбца на обратный ему;
3)складываем элементы столбца из обратных величин;
4)делим каждый из этих элементов на полученную сумму.
3-й способ:
1)суммируем элементы каждого столбца;
2)делим элементы каждого столбца на их сумму;
3)складываем элементы каждой строки полученной матрицы;
4)записываем результат в столбец;
5)делим каждый из элементов последнего столбца на порядок исходной матрицы п.
4-й способ:
1)перемножаем элементы каждой строки и записываем полученные результаты в
столбец;
2)извлекаем корень п-й из каждого элемента найденного столбца;
3)складываем элементы этого столбца;
4)делим каждый из этих элементов на полученную сумму.
Применив каждый из этих четырех способов к идеальной матрице, мы получим один и тот же точный результат. В применении у обратно симметричной, но не согласованной матрице ни один из указанных способов не дает собственного вектора. Тем не менее, эти способы можно использовать для обратно симметричных матриц, близких к согласованным. В результате будут получаться приближенные собственные значения.
Вычисление собственного значения. Если мы хотим проверить, является ли вектор х собственным вектором матрицы А, следует поступить так:
1) умножить матрицу А на этот вектор
a11 |
... a1n |
|
x1 |
y1 |
, |
|||||||
.............. |
|
.... |
= .... |
|||||||||
a |
n1 |
... a |
nn |
|
x |
|
y |
|
|
|||
|
|
|
|
n |
|
n |
|
|||||
2) |
разделить элементы полученного вектора у на соответствующие элементы вектора |
|||||||||||
х: |
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
, …, |
yn |
, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
||
1 |
|
|
n |
|
|
|
|
|
|
|
||
и если |
|
|
|
yn |
|
|
|
|
|
|||
|
y1 |
= …= |
, |
|
|
|
(18.1) |
|||||
|
|
|
|
|
||||||||
|
x |
x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
n |
|
|
|
|
|
|
то это отношение и есть собственное значение матрицы А, отвечающее данному вектору х. Если же хотя бы одно из равенств (18.1) нарушается, то вектор х не является
собственным вектором матрицы А.
Для четырех приближенных способов мы считаем результат приближением собственного вектора, поэтому ожидать выполнения даже одного из равенств (18.1) не следует. Поэтому поступают так. Считая каждое из отношений в (18.1) приближением к искомому собственному значению, выберем в качестве собственного значения их среднее арифметическое:
~ |
1 |
n |
y |
|
λmax = |
n |
∑ |
i |
. |
x |
||||
|
|
i=1 |
i |
|
18.2. Вычисление величины приоритетов
Сначала вычисляются величины локальных приоритетов (коэффициентов важности), а затем – альтернатив. Расчеты ведутся для матриц попарных сравнений критериев и
88
альтернатив, сформированных на втором этапе [2,11,28]. В результате расчета величин приоритетов критериев формируется собственный вектор w. Компоненты wj, j = 1,…, m, можно определить любым из четырех способов. Например, для четвертого способа
|
|
|
m |
1/ m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∏ w js |
|
|
||
w |
= |
s = 1 |
|
. |
(18.2) |
||
|
|
||||||
j |
|
m |
|
m |
1/ m |
|
|
|
|
∑ |
∏ |
wjs |
|
|
|
|
|
j=1 s = 1 |
|
|
|
||
Из выражения (18.2) следует, что числитель представляет собой абсолютное значение величины приоритета (коэффициента важности) j-го критерия. В знаменателе формулы находится сумма абсолютных значений величин приоритетов всех критериев.
Величины приоритетов рij каждой альтернативы рассчитываются для каждого критерия, они образуют матрицу, элементы которой вычисляются для четвертого способа по формуле
|
|
|
n |
|
1/ n |
|
|
|
|
∏ p |
|
|
|
||
|
|
|
|
irj |
|
|
|
рij = |
r = 1 |
|
|
. |
(18.2) |
||
|
|
1/ n |
|||||
|
n |
|
n |
|
|
|
|
|
∑ |
|
∏ |
|
|
|
|
|
|
|
pirj |
|
|
||
|
i=1 |
r = 1 |
|
|
|
|
|
Общий вид формулы (18.2) идентичен (18.1). Это означает, что рij является нормированным значением величины приоритета i-й альтернативы для j-го критерия.
18.3. Определение наилучшей альтернативы
Для расчета глобальных приоритетов на основе матрицы локальных приоритетов альтернатив и вектора локальных приоритетов критериев формируется (п х т)-матрица
(рijwj), элементы которой получаются умножением элементов рij матрицы локальных
приоритетов альтернатив на соответствующие элементы wj вектора-столбца локальных приоритетов критериев. По полученной матрице рассчитывается вектор глобальных
приоритетов (предпочтительностей альтернатив) рi:
m
рi = ∑pijwj . j=1
Решения соответствуют наибольшим значениям элементов вектора глобальных приоритетов альтернатив. Из их числа ЛПР выбирает одно предпочтительное решение. Если имеется решение, значительно превосходящее по величине приоритета остальные, то это решение выбирается в качестве предпочтительного.
18.4. Проверка согласованности
При заполнении матриц парных сравнений возможны следующие ошибки:
•нарушение транзитивности: из аij > аjk, аjk > аis может не следовать аij > аis;
•нарушение согласованности аik аkl ≠ аil.
Для обнаружения несогласованности можно использовать следующие количественные показатели:
•наибольшее собственное значение матрицы суждений λmax;
•индекс согласованности (ИС);
•отношение согласованности (ОС).
89
Если элементы положительной обратно симметричной и согласованной матрицы А изменить незначительно, то максимальное собственное значение λmax изменится
незначительно. Если λmax = п, то матрица А – согласованная. Если λmax ≠ п, то в качестве степени отклонения положительной обратно симметричной матрицы А от согласованной
можно взять отношение |
λmax −n |
, которое называется индексом согласованности (ИС) |
|
n −1 |
|
матрицы А и является показателем близости этой матрицы к согласованной. Считается, что если ИС не превышает 0,10, то степень согласованности суждений можно считать удовлетворительной.
Общая согласованность (ОС) рассчитывается по формуле [11] ОС = ИС / СС,
где СС – средняя согласованность для матриц разного порядка, значения которой приведены в табл. 18.1.
Таблица 18.1
Значения средней согласованности для матриц разного порядка
Размер матрицы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Значение СС |
0 |
0 |
0,58 |
0,90 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
Величина ОС должна быть не более 0,10, а в исключительных случаях – не более 0,20. Если же она больше этих значений, то необходимо уточнить таблицы попарных сравнений или декомпозицию проблемы в иерархию.
18.5. Пример применения метода анализа иерархий
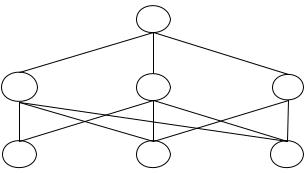
Рассмотрим пример практического применения метода анализа иерархий [28]. Предположим, что нам необходимо разрешить проблему распределения энергии в некоторой развитой стране между ее тремя крупнейшими пользователями: бытовым потреблением (БП), транспортом (ТР) и промышленностью (ПР). Они составляют третий, или низший, уровень иерархии. Целями, по отношению к которым оцениваются эти потребители, являются вклад в развитие экономики (Э), вклад в качество окружающей среды (С) и вклад в национальную безопасность (Б). Цели составляют второй уровень иерархии. Общая цель – благоприятное социальное и политическое положение (Бл), определяющие первый уровень иерархии (рис. 18.1).
Бл
Э |
С |
Б |
БП |
ТР |
ПР |
Рис. 18.1 Трехуровневая иерархия для проблемы распределения энергии
Построим матрицу попарных сравнений трех целей Э, С и Б в соответствии с их воздействием на общую цель – Бл. Зададим согласованную матрицу:
90
Бл |
Э |
С |
Б |
Э |
1 |
5 |
3 |
С |
1/5 |
1 |
3/5 |
Б |
1/3 |
5/3 |
1 |
Максимальное собственное значение этой матрицы λmax=3,00, индекс согласованности ИС = 0,0.
Вектор-столбец приоритетов, вычисленный любым из описанных выше способов, имеет вид
= 0,65 . w 0,130,22
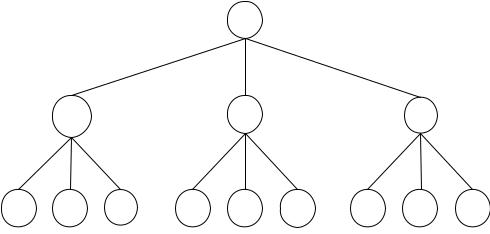
Следовательно, в соответствии со сравнением по социально-политическому влиянию экономика получает приоритет 0,65, окружающая среда – 0,13 и национальная безопасность – 0,22 (рис. 18.2).
|
|
|
|
|
|
Бл |
|
|
|
|
|
|
|
|
0,65 |
|
0,13 |
|
0,22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Э |
|
|
|
С |
|
|
|
Б |
|
0,65 |
0,23 |
0,12 |
|
0,59 |
0,33 |
0,08 |
|
0,54 |
0,30 |
0,16 |
|
БП |
|
ТР |
ПР |
БП |
|
ТР |
ПР |
БП |
|
ТР |
ПР |
Рис. 18.2. Значения приоритетов критериев и альтернатив Проведем теперь оценку относительной важности каждого потребителя с точки зрения
экономики, окружающей |
среды и |
национальной |
безопасности, составляющих второй |
||||||
уровень иерархии. |
|
|
|
|
|
|
|
|
|
Соответствующие матрицы попарных сравнений, индексы согласованности и вектора |
|||||||||
приоритетов имеют следующий вид: |
|
|
|
|
|
|
|||
|
Э |
|
БП |
ТР |
ПР |
|
w |
|
|
|
БП |
|
1 |
3 |
5 |
0,65 |
|||
|
ТР |
|
1/3 |
1 |
2 |
|
0,23 |
||
|
ПР |
|
1/5 |
1/2 |
1 |
|
0,12 |
|
|
|
|
|
|
||||||
|
|
|
|
λmax=3,00; ИС = 0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
БП |
ТР |
ПР |
|
w |
|
|
|
БП |
|
1 |
2 |
7 |
0,59 |
|||
|
ТР |
|
1/2 |
1 |
5 |
|
0,33 |
|
|
|
ПР |
|
1/7 |
1/5 |
1 |
|
0,08 |
|
|
|
|
|
|
||||||
|
|
|
|
λmax=3,01; ИС = 0,01 |
|
|
|
|
|
91
