Выбор метода прогноза зависит от множества факторов. Отметим некоторые из них: наличие данных, планируемый момент исполнения и желаемая точность прогноза, а также временны'е и стоимостные затраты на его составление.

Многие методы прогноза требуют наличия значительного количества исходных данных. Другие разрабатывают прогноз при отсутствии достоверной количественной информации. Существующие методы прогнозирования можно условно разбить на две группы: 1) количественные и 2) качественные.

Качественные, или экспертные методы строятся на использовании мнений специалистов в соответствующей области (экспертов).

Количественные методы основаны на обработке числовых данных и, в свою очередь, разделяются на каузальные, или причинно-следственные методы и методы анализа временных рядов (ВР). Каузальные методы применяются в тех случаях, когда искомое состояние зависит не только от времени, но и от нескольких переменных. Отыскание математических связей (уравнений и/или неравенств между объясняющими переменными Х и результирующими показателями Y) является целью каузальных методов.

Остановимся на описании особенностей каждого из перечисленных выше методов прогноза.

11.1. Анализ временных рядов

11.1.1. Модель временного ряда

Последовательность случайных наблюдений y1, y2, …, yТ, полученная в фиксированные моменты времени 1, 2,…, Т, называется временным рядом. Его простейшей вероятностной моделью является модель

yt = dt + εt ,

где dt – детерминированная составляющая, εt – случайная составляющая.

Под детерминированной (закономерной) составляющей временного ряда y1, y2, …, yп

мы будем понимать числовую последовательность d1, d2, …, dп, элементы которой dt вычисляются по определенному правилу как функция времени t.

Детерминированная составляющая часто отражает действия каких-либо определенных факторов или причин. Однако для многих ВР в различных областях науки и техники причины, порождающие их закономерные составляющие, могут быть не столь ясными. Тем не менее, их совокупное влияние может быть устойчивым в течение довольно длительных промежутков времени. Это обеспечивает возможность прогноза для подобных временных рядов. Если мы полностью выявим закономерную составляющую в поведении ВР, то оставшаяся часть выглядит хаотично и непредсказуемо. Ее обычно именуют иррегулярной,

или случайной компонентой временного ряда. Обозначим эту компоненту через ε1 ,…, εt ,…,

εn .

Аддитивная и мультипликативная модели. Формы разложения (декомпозиции)

временного ряда на детерминированную и случайную компоненты могут различаться. Укажем наиболее простые из них.

Аддитивной моделью временного ряда называется представление ряда в виде суммы детерминированной и случайной компонент, а именно:

yt = dt + εt при t = 1,...., n или X = D + E.

Мультипликативной моделью ВР называется представление ряда в виде произведения детерминированной и случайной компонент, а именно:

yt = dt × εt при t = 1,...., n или X = D + E.

57

11.1.2. Тренд, сезонная и циклическая компоненты

В детерминированной компоненте ВР dt обычно выделяют три составляющих части: тренд trt , сезонную компоненту st и циклическую компоненту ct . Рассмотрим аддитивную модель ВР. Мы можем записать:

+ st + ct при t = 1,...., n.

Тренд. Анализ временного ряда обычно начинается с выделения именно этой компоненты. Выделение тренда позволяет перейти к дальнейшей идентификации других компонент ВР.

Трендом временного ряда trt при t = 1,...., n называют плавно изменяющуюся, не

циклическую компоненту, описывающую чистое влияние долговременных факторов, эффект которых сказывается постепенно.

Сезонная компонента. Сезонная компонента отражает повторяемость процессов во времени. Она часто присутствует в экономических, метеорологических и других ВР. Сезонная компонента чаще всего служит источником краткосрочных колебаний временного ряда, так что ее выделение заметно снижает вариацию остаточных компонент.

Сезонная компонента st временного ряда при t = 1,...., n описывает поведение,

изменяющееся регулярно в течение заданного периода (года, месяца, недели, дня и т.д.). Она состоит из последовательности повторяющихся циклов.

Главная идея подхода к анализу сезонных компонент заключается в переходе от сравнения всех значений временного ряда между собой к сравнению значений через определенные промежутки времени. Это позволяет снизить оценку вариации ВР около своего среднего значения.

Циклическая компонента занимает промежуточное положение между закономерной и случайной составляющими ВР. Тренд – это плавные изменения, проявляющиеся на больших временных промежутках, а сезонная компонента – это периодическая функция времени, ясно видимая, когда ее период много меньше общего времени наблюдения. Под циклической компонентой обычно подразумевают изменения временного ряда, достаточно плавные и заметные для того, чтобы не включать их в случайную составляющую, но такие, которые нельзя отнести ни к тренду, ни к периодической компоненте.

Циклическая компонента ct временного ряда описывает длительные периоды

относительного подъема и спада. Они состоят из циклов, которые меняются по амплитуде и протяженности.

Изучение циклической компоненты полезно для прогнозирования (особенно краткосрочного).

Модели тренда. Приведем модели трендов, наиболее часто используемые при анализе

практических задачах редко превышает 5;

логарифмическая: trt = exp(b0 + b1t). Эта модель чаще всего применяется для данных,

имеющих тенденцию сохранять постоянные темпы прироста; логистическая: trt = а / (1 + b e−ct );

Гомперца: log(trt ) = a – b·rt , 0 < r < 1,

58

компонента представляет собой косинусоидальную функцию с амплитудой a, частотой ω, периодом 2π/ω и фазой θ. Величины a, ω, θ являются константами.

11.1.3. Декомпозиция временного ряда

Декомпозиция временного ряда заключается в выделении во временном ряде его компонент: тренда, сезонной и циклической составляющих. После их исключения временной ряд должен стать стационарным.

Выделение тренда. Для оценки и удаления тренда из ВР чаще всего используется метод наименьших квадратов [1]. Значения временного ряда yt рассматривают как зависимую переменную (отклик), а время t – как независимую переменную (фактор, влияющий на отклик):

yt = f (ti , θ) + εi , i = 1,…, n,

где f – функция тренда (она обычно предполагается гладкой), θ – неизвестные нам параметры (параметры модели временного ряда), εi – независимые и одинаково

распределенные случайные величины, распределение которых мы предполагаем нормальным. Метод наименьших квадратов состоит в том, что мы выбираем функцию тренда так, чтобы

Для простого линейного тренда (11.1) с помощью метода наименьших квадратов по

t=1

Выделение сезонных эффектов. Для выделения сезонной компоненты есть несколько способов. Их выбор обычно определяется моделью подбираемого временного ряда.

Рассмотрим две распространенных модели ВР. Первая из них включает в себя тренд (trt ),

Сезонные эффекты на фоне тренда. Предположим, что рассматриваемый временной ряд y1, y2, …, yп может быть описан аддитивной моделью (11.2). Пусть р – период

последовательности st , так что st = st+ p для всякого t. Необходимо оценить значения st по наблюдениям yt при том, что величина р известна.

59

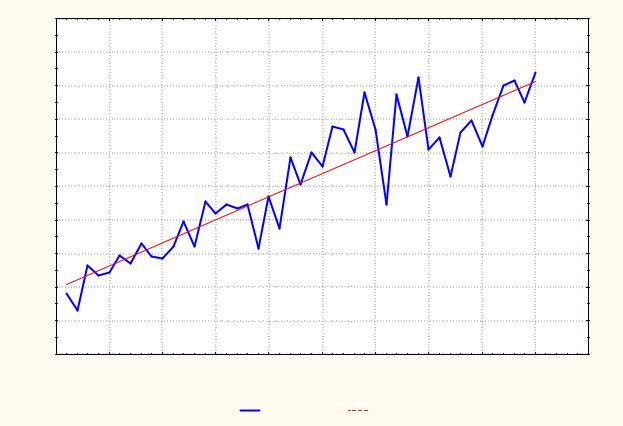
Рис.11.1. Исходный временной ряд и линейный тренд

Для этого сначала мы должны оценить тренд trt . Это можно сделать с помощью

Каждое из этих отклонений yi от trˆi можно рассматривать как результат влияния сезонных изменений. Усреднение этих разностей дает нам оценку сезонной компоненты si . В качестве простейшей оценки можно взять среднее арифметическое, т.е. положить

l=0

Вкачестве других оценок sˆi можно взять взвешенное среднее, медиану и т.д.

Перечисленные характеристики уменьшают влияние резко выделяющихся наблюдений. Метод скользящих средних. При наличии в ряде циклической компоненты расчет

сезонных эффектов несколько отличается от описанного выше. В этом случае для выяснения сезонных вкладов необходимо оценить не только тренд, но и циклическую компоненту. Проще всего одновременно оценить тренд и циклическую компоненту можно с помощью скользящего среднего (СС).

Метод скользящего среднего основан на переходе от начальных значений ряда к их средним значениям на интервале времени, длина которого выбрана заранее. При этом сам выбранный интервал скользит вдоль ряда. В методе СС можно использовать различные виды усреднения значений ряда: среднее арифметическое (простое или с весами), медианы и др. К медианному сглаживанию прибегают тогда, когда среди наблюдений есть выбросы.

60