Правило классификации на основании апостериорных вероятностей

Для принятия решения об отнесении объекта с описанием Х к классу Ωi , i = 1,…, m,

можно использовать байесовский подход, который заключается в вычислении и сравнении апостериорных вероятностей Р ( Ωi | х) принадлежности объекта классу Ωi . В этом случае решающее правило формулируется следующим образом:

При предположениях нормальности распределений и равенства ковариационных матриц для т = 2 классов апостериорные вероятности равны

Если параметры нормальных распределений неизвестны, эти вероятности могут быть оценены по данным обучающей выборки как

где v – значение функция классификации u (x) (8.2) после подстановки в нее оценок (8.7) и (8.8), полученных по обучающей выборке.

классифицируемое наблюдение будет относиться к тому классу, расстояние Махаланобиса до центра которого минимально

8.3. Ошибка решающего правила

Для определения ошибки решающего правила классифицируем экзаменационную выборку с помощью построенного решающего правила и вычислим частоту ошибочных решений. Результаты вычислений представляются в виде матрицы классификации, строками которой являются номера классов в экзаменационной выборке (наблюдаемый класс), а столбцами – решение, полученное на основании решающего правила (предсказанный класс).

Лекция 9. Древообразные классификаторы

9.1. Назначение древообразных классификаторов

Древообразные классификаторы применяются при классификации в случае, когда классы описаны путем указания всех входящих в них наблюдений. Число классов может быть произвольным. Задача принятия решения (выбора варианта действия из m ≥ 2 возможных) на основе древообразных классификаторов заключается в определении номера класса, к которому относится классифицируемое наблюдение. Деревья классификации – это способ представления правил классификации, на основании которых принимается решение, в виде иерархической структуры.

Рассмотрим случай двух классов:

46

где xk – вектор возможного значения наблюдения,

yk = 1, если наблюдение (объект) принадлежит первому классу, yk = 2, если

наблюдение (объект) принадлежит второму классу.

Будем считать, что новые наблюдения извлекаются наудачу и независимо друг от друга из ряда (9.1).

В основе описываемого метода лежит понятие бинарного дерева – графа. Эти деревья приято изображать в перевернутом виде: корень сверху, листья – внизу. Под словом «корень» понимаем самый верхний узел (вершину графа). Под словом «лист» понимается узел, из которого не выходят дуги (ребра) к расположенным ниже узлам (терминальный узел).

С каждым узлом t дерева связаны следующие объекты [15]: Rt – подмножество пространства наблюдений (R);

Vt – подмножество генеральной совокупности (9.1) с xk Rt ;

At – правило классификации из разрешенного набора правил для Х Rt .

Кроме того, для нетерминальных узлов вводится правило разбиения на два подмножества Rl(t) и Rr(t) таких, что Rl(t) Rr(t) = Rt и Rl(t) ∩ Rr(t) = Ο.

Древообразные классификаторы определяются рекурсивно. Для этого задаются

•критерий качества классификации на Rt ,

•разрешенный класс правил для построения At ,

•способ построения Rl(t) и Rr(t) ,

•способ объявления узла листом, т. е. правило прекращения последовательных разбиений. В качестве корневого (нулевого) узла принимается узел с R0 , совпадающий со

решения о типе урагана. Данные представляют собой значения двух координат: долготы (Longitude) и широты (Latitude), при которых 37 штормов достигли ураганной силы. Штормы классифицируются как ураганы двух типов, возникающие в Северной Атлантике: BARO (бароклинические) и TROP (тропические).

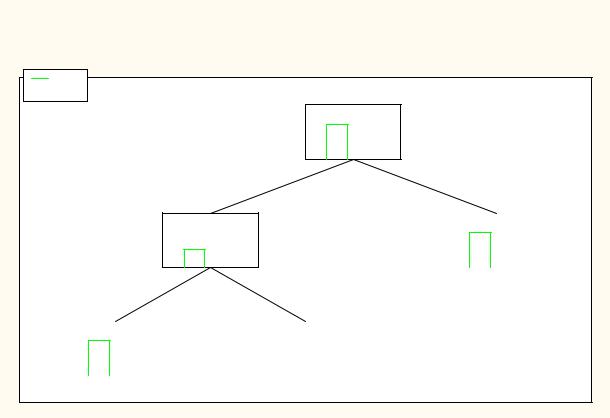
Ниже приводится дерево классификации (рис. 9.1).

Заглавие графа дает итоговую информацию о том, что дерево классификации имеет два разбиения и три терминальных узла. Терминальные узлы, или, как их иногда называют, листья, представляют собой узлы, в которых не принимается решение о дальнейшем разбиении. На графе терминальные узлы отмечаются пунктирной красной линией, в то время как остальные узлы решения отмечаются сплошной черной линией.

Построение дерева начинается с узла, называемого корнем. На графе он помечается цифрой 1 в левом верхнем углу. Первоначально все 37 ураганов приписываются корневому узлу и временно классифицируются как ураганы типа BARO, как указано меткой BARO в правом верхнем углу корневого узла. Тип BARO выбран в качестве начальной классификации, так как ураганов этого типа несколько больше, чем ураганов типа TROP. Это можно увидеть на гистограмме, расположенной внутри корневого узла. Легенда, идентифицирующая, какие столбцы гистограммы соответствуют ураганам типов BARO и TROP, расположена в верхнем левом углу графа.

47

Рис. 5.1. Дерево классификации

Корневой узел разбивается, образуя два новых узла. Текст, находящийся ниже корневого узла, описывает условие разделения. В нем указано, что ураганы со значением координаты долгота (Longitude) меньше или равным 67,75, относятся к узлу 2 и предварительно классифицируются как ураганы типа TROP, а ураганы со значением координаты долгота (Longitude) больше 67,75, приписываются к узлу 3 и классифицируются как ураганы типа BARO. Значения 27 и 10, напечатанные над узлами 2 и 3 соответственно, указывают число наблюдений (объектов), отнесенных к каждому из этих двух дочерних узлов из их родительского (корневого) узла. Аналогичным образом производится разбиение в узле 2. В результате 9 ураганов со значением координаты долгота (Longitude) меньше или равным 62,5, относятся к узлу 4 и классифицируются как ураганы типа BARO, а остальные 18 ураганов со значением координаты долгота (Longitude) больше 62,5, приписываются к узлу 4 и классифицируются как ураганы типа TROP.

В каждом узле строится гистограмма распределения объектов по классам. Информация, связанная с построением дерева, представлена, в табл. 9.1.

48