8.16. Геометрическое представление сигналов и помех

Совокупность трех чисел , , может быть представлена как координаты вектора в трехмерном пространстве. Аналогично отсчетов, определяющих сигнал, можно представить себе как координаты вектора в воображаемом -мерном пространстве.

Свойства -мерного пространства в значительной степени являются обобщением свойств двух- и трехмерного пространств. Длина ( вектора определяется его нормой :

Таблица 8.1 – Параметры векторов в непрепывном и дискретном пространствах.

Параметры	Эвклидово пространство, n-конечно	Гильбертово пространство, n-бесконечно
(длины вектора)
(расстояние между векторами)
(скалярное произведение)

Фазовый сдвиг между и :

не может быть больше 1:

Неравенсво Шварца-Буниковского:

Расстояние между двумя векторами и определяется как норма разности векторов:

Скалярное произведение двух векторов:

Координаты вектора представляют собой проекцию вектора на оси. Если обозначить угол мнежду векторами через , то получим выражение (фазовый сдвиг):

а для проекций на и обратно на :

Пространство непрерывных функций (сигналов), заданных на интервале 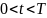, имеет бесконечное число измерений. Для такого пространства скалярное произведение двух векторов определяется соотношением (функция взаимной корреляции):

а норма и расстояние между векторами:

Пространство с бесконечным числом измерений прдставляет собой естественное обобщение -мерного пространства, полученного путем предельного перехода от дискретной последовательности к функции непрерывного аргумента. Отметим, что нормы векторов равны корням из их мощностей, а скалярное произведение является мерой корреляции этих сигналов. Сигналы конечной длительности , ограниченные полосой 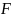, геомет­ри­­чески представляются различными векторами в n-мерном пространстве. Различие между двумя какими-либо сигналами выражается расстоянием между векторами. Это расстояние зависит от длин векторов и угла между ними, а косинус есть не что иное, как коэффициент взаимной корреляции сигналов.

Рисунок 8.60. Векторное представление сигналов и помехи

Полное отсутствие корреляции (т.е. равенство нулю коэффициента корреляции) выражается ортоганальностью векторов ( ).

Помеха, ограниченная той же полосой, что и сигнал, также определяется вектором в n-мерном пространстве. Этот вектор добавляется к вектору сигнала. В отличие от вектора сигнала, вектор помехи может иметь любые величину и направление (вектор случайный). В результате при наложении помехи на сигнал вокруг конца вектора сигнала образуется «облако», переменная плотность которого выражает вероятность попадания результрующего вектора (вектор принятого сигнала) в данный элемент объема. Для флуктуационной помехи это «облако» имеет сферическую форму с эффективным радиусом

где – мощность помехи.

Сообщение (видиосигнал) , не содержащее колебаний с частотой выше , так же, как и сигнал, может быть представлено в m-мерном пространстве, где . Совокупность возможных сообщений определяет это пространство (пространство сообщений). На следующем рисунке представлена двухмерная модель этого пространства и двумя различными сообщениями и .

Рисунок 8.61. Векторное представление сигналов и помехи

При передаче сообщения преобразовывается в сигнал с использованием некоторого переносчика . Математически эту операцию формирования сигнала можно представить в виде

где – оператор, в общем случае нелинейный. Теоретически формирование сигнала может быть представлено как преобразование пространства сообщений в пространство сигналов : векторы и пре­об­ра­зуются в векторы и .

Мерность пространства сообщений в общем случае не равна мерности сигналов . При однополосной передаче 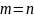. В случае амплитудной модуляции сигналы имеют вдвое большее число координат, чем сообщений: , а при частотной пространство сигналов имеет значительно большее число измерений, чем пространство сообщений.

При наложении помехи на сигнал создается область неопределенностей, в которую попадают принятые сигналы Взаимодействие сигнала и помехи можно выразить оператором

Оператор преобразует пространство сигналов в пространство принятых сигналов : векторы и переходят в и .

Приемник по принятым сигналам 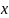воспроизводит переданное сообще-ние т.е. преобразует пространство сигналов в пространство принятых сообщений .

Если помеха отсутствует, то принятый сигнал преобразуется в сообщение обратным оператором В этом случае принятие сообщения соответствует (тождественно) переданному.

При наличии помех сообщения на приеме воспроизводятся с ошибкой, вместо может быть воспроизведено и наоборот. Ошибка произойдет, когда результирующий вектор окажится ближе к концу вектора того сигнала, который в данный момент не передается. Можно построить приемник, воспро-изводящий сообщение всякий раз, когда конец вектора бли-же к концу вектора , чем к концу вектора и наоборот. Такой приемник по Котельникову называется идеальным или оптимальным. Очевидно, ошибка при оптимальном приеме будет тем меньше, чем больше расстояние между соседними сигналами.