8.12. Огибающая и фаза узкополосного гауссовского случайного про­цесса и суммы гармонического сигнала и узкополосного гауссовского слу­чайного сигнала

1. Огибающая и фаза узкополосного гауссовского случайного процесса.

Рисунок 8.34. Временная и вероятностная характеристики огибающей СП

Если процесс стационарный, то каждую реализацию можно разложить на квадратурные составляющие:

или

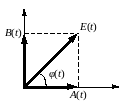
Рисунок 8.35. Разложение огибающей СП на квадратурные составляющие

Считаем, что процесс не содержит постоянной составляющей

а мощности квадратурных составляющих одинаковы:

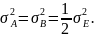
Поскольку – нормальный (гауссовский) процесс, то , и 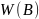имеют нормальное распределение:

а их функция корреляции в совпадающие моменты времени . Найдем плотность вероятности огибающей и фазы

Рисунок 8.36. Сущность округления огибающей и фазы при нулевой средней

В прямоугольных координатах (рис. 8.36) вероятность того, что случай­ная величина будет находиться в пределах прямоугольника, ограниченного сторонами и можно выразить через совместную плот­ность вероятности:

Вероятность этого же события можно записать в полярных координата и , т.е.

следовательно:

Поскольку речь идет об одной и той же вероятности, то площадь элементарного прямоугольника должна быть равной элементарной площади в полярных координатах:

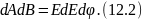
Кроме того, вследствие статической независимости квадратурных составляющих, а также их и , с учетом (12.2):

Сопоставляя (12.1) и (12.3), можно получить:

Выражение (12.4) определяет совместную плотность вероятности оги­бающей и фазы . Для определения плотности вероятности огибающей проин­тегрируем (12.4) по всем возможным значениям в пределах от 0 до :

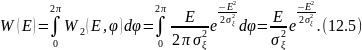
Для определения плотности вероятности фазы надо совместную плотность (12.4) проинтегрировать по всем возможным значениям огибающей:

Из (12.6) видно, что плотность вероятности фазы равномерна по всей об­ласти возможных значений от до (рис. 8.37).

Рисунок 8.37. ФПВ огибающей и фазы СП при нулевой средней

Выражение (12.6) может быть безразмерным, если обозначить .

При переходе от к должно выполняться равенство:

Подставляя в (12.7) значение 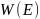из (12.5) и учитывая , полу­чим:

Плотность вероятности, определяемая (12.8), называется распределением Рэлея.

Здесь переменная может принимать лишь неотрицательные значения, в отличии от нормального распределения, где может принимать и положитель­ные, и отрицательные значения. Из рис. 8.37 видно, что максимальное значение плотности вероятности огибающей имеет место при или, что тоже самое, .

Кроме того, хотя в рассматриваемом процессе нет постоянной состав­ляющей, среднее значение огибающей не равно 0.

2. Огибающая и фаза суммы гармонического колебания и узкополосного гауссовского случайного сигнала.

Задача решается аналогично. Пусть имеется сумма узкополосного нор­мального стационарного процесса и гармонического сиг­нала .

В этом случае:

Аналогично находятся , и :

Рисунок 8.38. Огибающая СП при нулевой и ненулевой средней

Если найти совместную плотность вероятности огибающей и фазы и про­интегрировать по фазе в пределах от до то придем к распределению Райса (или обобщенно Рэлея) для плотности вероятности огибающей суммы сигнала и шума:

функция Бесселя нулевого порядка.

При , – получим распределение Рэлея как частный случай.

При распределение стремится к нормальному (с ненулевым сред­ним).

Рисунок 8.39. ФПВ огибающей при различных

Рисунок 8.40. ФПВ фазы при различных U₀/σ_ξ

Чем больше амплитуда сигнала, тем ближе фаза результирующего коле­бания к фазе этого сигнала.