7.7. Функция корреляции одиночного прямоугольного импульса

Случайные процессы могут быть периодическими и непериодическими.

Функция корреляции нерперывного процесса

Рисунок 7.14. Сущность вычисления функции корреляции

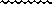
Считаем, что процесс эргодический: .

Напишем функцию корреляции отдельно для ( ) и ( ):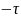

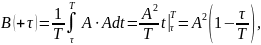
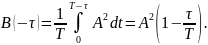
Окончательно:

Функция корреляции четная.

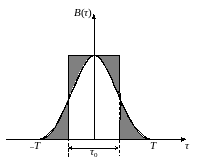
Рисунок 7.15. Функция корреляции непериодического сигнала

Функция корреляции периодического сигнала

ДАМ:

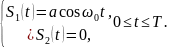
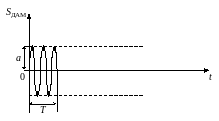
Рисунок 7.16. Временное представление периодического сигнала

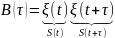
– функция корреляции в общем виде.

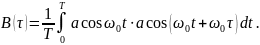
Учитывая элементарные тригонометрические преобразования, в результате получим:

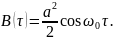
Функция корреляции будет иметь вид:

Рисунок 7.17. Функция корреляции периодического сигнала

Вывод:

У периодического сигнала функция корреляции является периодической фукцией той же частоты .

7.8. Применение корреляционных методов обработки сигналов в технике связи

Устройства позволяющие определить функцию корреляции сигнала называются корреляционными. Они широко используются для обработки сигналов на приеме с целью принятия решения о переданном сигнале.

Два основных способа приема:

1) взаимнокорреляционный прием;

2) автокорреляционный прием.

Все взаимнокорреляционные способы приема основываются на вычисле­нии .

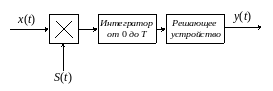
Рисунок 7.18. Структурная схема взаимнокорреляционного приемника

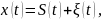
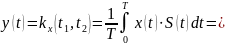
где – переданный сигнал,

– принятый сигнал,

– помеха.

Автокорреляционный приемник

Рисунок 7.19. Структурная схема автокорреляционного приемника

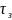– задержка на один элемент сигнала.

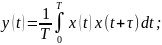
0 0

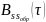– функция автокорреляции сигнала,

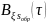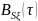, – функции взаимной корреляции,

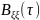– функция автокорреляции помехи.

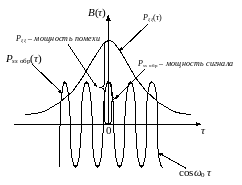
Рисунок 7.20. Сущность выделения слабого сигнала на фоне помех

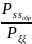растет, если увеличивается.

Чем больше , тем лучше (больше отношение мощности сигнала к помехе).

Данный способ приема называется выделением сигнала на фоне помех.

Часть II. Теория передачи сигналов

8. Случайные сигналы

8.1. Энергетический спектр случайных сигналов

При наблюдении за течением случайного процесса (СП) мы можем опре­делить лишь текущий спектр данной реализации , т.е.

Рисунок 8.1. Реализация случайного процесса

Функция (8.1) случайная, поэтому удобно ввести неслучайную функцию – энергетический спектр.

Энергетический спектр стационарного случайного процесса определяется как спектр его функции корреляции.

Прямое преобразование Фурье:

Обратное преобразование Фурье:

Пара преобразований, связывающая функции и , носит наз­вание преобразование (теорема) Винера-Хинчина. Т.к. и – четные функции своих аргументов, то формулы можно записать в другом виде:

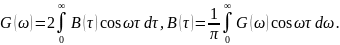
Физический смысл функции легко выяснить, если положить , то­гда

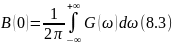
или

где – полная мощность процесса.

Поэтому энергетический спектр часто называют спектром мощности СП.

Формула (8.2) показывает, что функция выражает спектральную плот­ность мощности процесса и, следовательно, имеет размерность 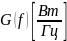, т.е. характеризует распределение мощности СП по частоте, это мощность СП в полосе частот 1 Гц.

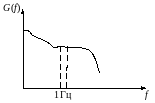
Рисунок 8.2. Спектральная плотность мощности (энергетический спектр СП)

Мощность случайного процесса в полосе или определяется следующим образом:

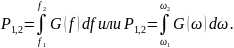
Энергетический спектр можно выразить через текущий спектр реализа­ции с помощью равенства Парсеваля: энергия сигнала определяется интегралом квадрата напряжения или интегралом квадрата модуля его спектральной плот­ности по частоте. Энергия процесса , выделяющегося за время , равна:

Средняя мощность процесса определяется как предел 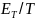при , т.е.

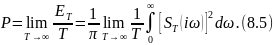
Сопоставляя (8.4) и (8.3), находим:

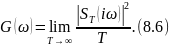
Это соотношение устанавливает связь между энергетическим спектром процесса и текущим спектром его реализации.