Теорема д. Стокса

Данная теорема позволяет рассчитывать циркуляцию вектора по контуру конечной длины с помощью ротора этого вектора.

Циркуляция векторного поля по замкнутому положительно ориентированному контуруL равна потоку ротора этого поля через любую гладкую поверхность S, опирающуюся на данный контур :

. (2.12)

Д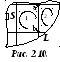ля доказательства теоремы рассмотрим контур с охватываемой им площадью (рис. 2.6). Весь контур разбивается на элементарные контуры той же ориентации (рис. 2.10).

Циркуляция по элементарному контуру равна .

Все смежные контура (1и2на рис. 2.10) имеют такую особенность: на общей границе при том же значении поля вклад в циркуляцию по каждому из смежных контуров будет происходить с изменением знака (для контура1-ab, а для2- ba). В результате вклад в циркуляцию всех внутренних участков контуров взаимно компенсируется, и нескомпенсированными останутся только участки принадлежащие контуруL, что в итоге дает (2.12) [8].

Частным случаем (2.12) в случае расположения контура на плоскости является формула Д. Грина (М. Остроградского- Д. Грина [9]):

. (2.13)

Формулы (2.12) и (2.13) позволяют свести вычисление криволинейного интеграла второго рода к вычислению двойного интеграла по области S.

Обратный переход по (2.12) осуществляется аналогично (2.8).

2.4. Оператор набла и оператор п. Лапласа

Написание формул векторного анализа упрощается при использовании оператора набла (оператора У. Гамильтона), представляющего собой вектор . Сам по себе этот вектор смысла не имеет, но позволяет компактно записать формулы (2.3), (2.5) и (2.9):

; ;. (2.14)

Кроме того, оператор набла позволяет упростить вычисление дифференциальных операторов более высоких порядков.

Следует отметить, что с  следует обращаться осторожно, а при его использовании нужно помнить о том, что данный оператор является не только векторным, но и дифференциальным.

Например, найдем . С помощью получаем . По правиламдифференцирования произведения оператор действует сначала на первый множитель, а затем на второй: . В результате получаем. Процедура вычисления через координаты вектора потребовала бы на порядок больше операций.

Попробуйте получить самостоятельно не включенную в (2.15) формулу для разложения . Правильный ответ приведен в концеприложения 1.

Некоторые тождества и операции второго порядка.

; ;

; ;

; ;

; . (2.15)

Оператор Лапласа(, лапласиан) является оператором второго порядка.

. (2.16)

Как и ,  применяется как к скаляру, так и к вектору.

. (2.17)

. (2.18)

В случае декартовой системы координат (2.18) упрощается [2]:

. (2.19)

Сведения о часто применяемых в теории ЭМП криволинейных системах координат (цилиндрической и сферической) и векторных операциях в них приведены в Приложении 2.

2.5. Классификация векторных полей

Векторное поле задано однозначно, если известны его ротор и дивергенция как функции пространственных координат.

В зависимости от значений данных функций различают потенциальное, вихревое (соленоидальное) поле и поле общего типа [2].

Векторное поле потенциально, если существует некоторая скалярная функцияU, которая связана сследующим образом:. ФункциюU называютскалярным потенциалом поля.

Необходимым и достаточным условием потенциальностиявляетсяравенство ротора нулю ().

Соленоидальным(вихревым) называется векторное поле, в каждой точке которого(необходимое и достаточное условие),.

Соленоидальное векторное поле можно представить как. В этом случае векторную величинуназываютвекторным потенциалом поля ().

Название поля данного типа можно объяснить тем, что оно было обнаружено в соленоиде, – катушке индуктивности (она может быть как с сердечником, так и без сердечника), длина которой значительно превышает диаметр.

Если у векторного поля и, то это –поле общего типа.

Произвольное векторное поле общего типа можно представить в виде суммы потенциальной и вихревой частей: , – где ввключеныисточники поля(), а в–вихри поля()[2].

Теперь, после изучения интегральных и дифференциальных операций и основных теорем векторного анализа, можно приступить к изучению базиса теории ЭМП – системы уравнений Максвелла.