14. Связь между продольными и поперечными составляющими эмп

В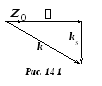олновое числоk ЭМВ, распространяющейся в направляющей системе вдоль оси z при наличии продольных составляющих векторов поля (см. подраздел 10.3), целесообразно разложить на поперечный (k_S) и продольный () волновые коэффициенты (рис. 14.1).

Из векторных соотношений получаем:

. (14.1)

Если потери в направляющей системе малы, то (14.1) запишется в виде:

. (14.2)

Волновые уравнения для поперечных составляющих ЭМП имеют вид:

; , (14.3)

где –оператор Гамильтона по поперечным координатам [11].

В линиях передачи удобно от векторных волновых уравнений перейти к скалярным для продольных и поперечных составляющих. При этом оказывается, что достаточно решить эти уравнения только для продольных составляющих Е_z и H_z, поскольку поперечные составляющие Е_ и H_ в направляющих системах являются однозначными функциями продольных.

Для вывода соотношений между продольными и поперечными составляющими ЭМП векторы поля и оператор набла разложим на продольную и поперечную составляющие:

; ; . (14.4)

Найдем проекции уравнений Максвелла в комплексной форме (3.16) и (3.17) на поперечную плоскость:

; . (14.5)

Представим ротор с учетом (14.4) в виде

, откуда следует

, (14.6)

где индекс  при grad означает, что дифференцирование производится только в поперечной плоскости. Аналогичное соотношение получается для .

С учетом (14.6) уравнения (14.5) запишутся в виде:

;

. (14.7)

Если второе уравнение (14.7) умножить векторно на , то получим (при двойном умножении поперечного вектора на орт он поворачивается в поперечной плоскости на 180) . Выразим произведение и подставим его в первое из уравнений (14.7); тогда . Учитывая (14.1), получаем выражение для поперечной электрической составляющей ЭМП [11]:

. (14.8)

Аналогично получается для магнитной составляющей:

. (14.9)

Поперечные составляющие поля пропорциональны градиентам Е_z и H_z, определяемым в поперечной плоскости. По аналогии можно утверждать, что Е_z и H_z являются потенциальными функциями Е_ и H_ [11].

В скалярной форме (14.8)-(14.9) в декартовой системе координат имеют вид:

;

;

;

. (14.10)

Аналогичным образом выводятся соотношения для поперечных составляющих ЭМП произвольных криволинейных систем координат, которые можно найти в [4].

Таким образом, при расчете ЭМП в направляющей системе сначала решают волновые уравнения для продольных составляющих, а затем при необходимости находят поперечные составляющие по (14.10) или обобщенным формулам [4].

Обычно для основных типов волн часть слагаемых в (14.10) отсутствует.

15. Телеграфные уравнения. Волновые уравнения для напряжения и тока

В линиях передачи Т-волны возможен переход от векторных величин и к скалярным величинам U (напряжение между проводниками 1 и 2) и I (ток):

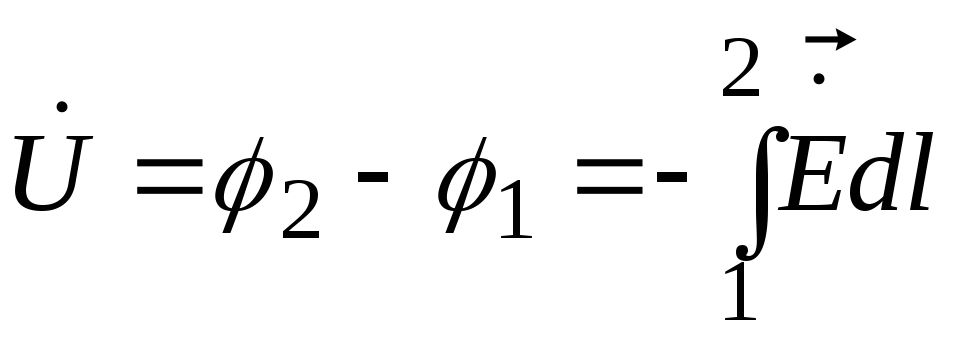; ; (15.1)

где L – замкнутый контур, охватывающий проводник с током.

Телеграфные уравнения выводятся из уравнений Максвелла (3.16) и (3.17). ЭМП Т-волны имеет только поперечные составляющие, поэтому достаточно определить проекцию ротора на поперечную плоскость S_:

. (15.2)

Следовательно, уравнения Максвелла для Т-волны принимают вид:

; . (15.3)

Продифференцируем обе части равенств (15.1) и подставим в них (15.3), предварительно заменив , где – нормаль к кривой интегрирования, лежащая в плоскости S_. Тогда:

;

. (15.4)

Интеграл от вектора магнитной индукции по кривой интегрирования представляет собой магнитный поток в пространстве между двумя проводниками, отнесенный к единице длины линии. Этот магнитный поток можно записать через собственную индуктивность единицы длины линии (12.26), (9.18).

Заметим, что L₀ соответствует внешней индуктивности, определенной для случая стационарных токов в линии, так как магнитный поток внутри проводников в идеальной линии отсутствует [11].

Интеграл от вектора электрической индукции по замкнутому контуру L представляет собой поток , отнесенный к единице длины линии, который по теореме Гаусса (3.3) равен линейной плотности заряда _l. Формулы электростатики (12.7) связывают _l с напряжением через емкость единицы длины линии [11].

Следовательно, уравнения Максвелла для линий передачи с Т-волной сводятся к известным из теории цепей телеграфным уравнениям:

; . (15.5)

Отсюда следует, что методы теории цепей дают правильные результаты для линии передачи без потерь и с пренебрежимо малыми потерями [11].

От уравнений (15.5) можно перейти к одномерным волновым уравнениям для напряжения и тока:

; . (15.6)

где волновое число .

Характеристическое сопротивление линии передачи без потерь

. (15.7)

Для учета потерь в диэлектриках и проводниках линии передачи в (15.5) вводят комплексные сопротивление и проводимость:

; , (15.8)

где R₀– погонное сопротивление проводников, аG₀– погонная проводимость изоляции линии передачи [11]. В этом случае (15.5) запишется в виде:

; , (15.9)

а волновое число .

Характеристическое сопротивление линии передачи с учетом потерь (15.8) определяется формулой (15.10).

. (15.10)

Решением волновых уравнений (15.6) для напряжения и тока являются соответственно прямые и обратные волны напряжения и тока, аналогичные (7.8):

; (15.11)

. (15.12)

Аналогичным образом выводятся коэффициенты затухания, фазы, отражения, прохождения и т. п [11].

Использование волновых величин U(z)иI(z)позволяет упростить анализ ЭМП в линиях передачиТ-волны, что широко используется в теории длинных линий и электродинамике [11].