13.5. Явление полного прохождения

Для ЭМВ с параллельной поляризацией существует угол падения, именуемый углом Д. Брюстера , при котором отраженная волна отсутствует, а значит, ЭМВ полностью переходит во вторую среду. Рассмотрим немагнитные диэлектрики () с малыми потерями (<<), исключив тривиальный случай равенства параметров сред ().

Согласно (13.14) при , поскольку .

По закону Снеллиуса (13.4) отсюда находим:

,

откуда следует

. (13.23)

Угол Брюстера можно найти для любого соотношения между и .

И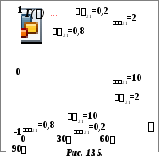з формул (13.10) вытекает, чтодля перпендикулярной поляризации (при ) угол полного прохождения между разнородными диэлектриками не существует, и всегда больше нуля. На рис. 13.5 приведены графики зависимостей коэффициента отражения ЭМВ обеих поляризаций от угла падения при различных соотношениях параметров диэлектрических сред [19].

Угол Брюстера называют также углом полной поляризации.

Если ЭМВ с произвольной поляризацией направлена на диэлектрическую пластину под углом , отраженный луч имеет только перпендикулярную поляризацию, так как параллельно поляризованная компонента полностью проходит через пластину [11].

Диэлектрические пластины и шайбы, служащие для герметизации и крепления в различных устройствах СВЧ, часто ставят под углом Брюстера. В этом случае в определенном диапазоне частот они полностью прозрачны для проходящих волн.

Аналогичным образом поступают, если необходимо обеспечить минимальный уровень отраженной волны при падении ЭМВ из воздуха на вещество с волновым сопротивлением, существенно отличающимся от волнового сопротивления воздуха.

13.6. Стоячая волна. Ксв. Кбв

При нормальном падении ЭМВ на границу раздела сред в первой среде складываются падающая и отраженная волны. Эти волны имеют противоположные направления распространения, а соотношение их амплитуд равно .

Суперпозиция ЭМВ в первой среде (рис. 13.2) с учетом (13.6) определяется следующим образом (для параллельной поляризации из (13.11) получаются аналогичные соотношения, только изменяется ориентация в пространстве и ):

,

. (13.24)

С учетом (13.5) выражения (13.24) можно преобразовать так:

,

. (13.25)

Выражение в квадратных скобках можно назвать множителем стоячей волны, поскольку данная величина показывает периодически изменяющуюся вдоль координатых«волнистую структуру» ЭМП (рис. 13.6). Рассмотрим данную величину при отсутствии потерь в среде[4].

. (13.26)

При монотонном изменении хвторое слагаемое (13.26) вращается вокруг «1» с удвоенной (по сравнению с падающей волной) частотой. Максимальное значение составляет , а минимальное . Расстояние между соседними экстремумами стоячей волны составляет/k₁=₁/2 [4].

Е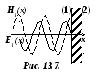сли среды согласованы, то , и в этом случае отраженная ЭМВ отсутствует. Если вторая среда идеальный проводник, то , и в этом случае будет отсутствовать прошедшая ЭМВ, а в первой среде будет только стоячая волна с удвоенной (относительно падающей ЭМВ) амплитудой.

Из (13.24) и (13.25) получаем :

, . (13.27)

На рис. 13.7 показана структура ЭМП стоячей волны. Из рис. 13.7 и (13.27) следует, что магнитная и электрическая составляющие имеют фазовый сдвиг на четверть длины волны (90). Среднее значение вектора Пойтинга в любой точке стоячей волны равно нулю, и передачи энергии нет[4].

На практике удобно оценивать неравномерность пространственного распределения ЭМП с помощью коэффициента стоячей волны (КСВ=1…при ) икоэффициента бегущей волны (КБВ=1…0):

; . (13.28)