§ 5.4. Математические модели реализаций случайных процессов

Для рассмотрения конкретных свойств систем бывает необходимо учесть особенности сигналов, циркулирующих по каналам связи этих систем. Такие особенности можно описать по-разному: просто перечислить возможные реализации (если число их конечно) либо задать в той или иной форме общие свойства реализаций, входящих в ансамбль. О дискретных процессах мы будем говорить отдельно (см. § 5.8), а сейчас рассмотрим математические модели реализаций непрерывных сигналов.

Приведем примеры, с которыми часто имеют дело в теории сигналов [7].

МОДЕЛИРОВАНИЕ КОНКРЕТНЫХ Реализаций

Гармонические сигналы. Обозначим через S_c множество всех синусоидальных сигналов:

S_с = {x: x(t) = S cos | ( t + )};  –  < t < ; S,  R⁺,   [0, 2]}. (1)

Здесь R⁺ – множество всех положительных действительных чисел; S на­зывается амплитудой,  – круговой частотой ( = 2,  – частота),  – фазой гармонического колебания.

Модулированные сигналы. В технических системах полезная информация может переноситься каким-нибудь одним параметром “гармонического” колебания. Конечно, колебание при изменении этого параметра во времени перестает быть гармоническим. Процесс изменения параметра синусоиды называется модуляцией, а выделение этого изменения в чистом виде, как бы “снятия” модуляции, называется демодуляцией. Само колебание называется несущим. Различают амплитудную, частотную и фазовую модуляцию в зависимости от того, на какой из параметров несущего колебания “накладывают” полезную информацию (параметры с индексом 0 считаются постоянными):

S_ам = {x: x(t) = S(t) cos (₀t + ₀)}, (2) S_чм = {x: x(t) = S₀ cos ((t)· t + ₀)}, (3) S_фм = {x: x(t) = S₀ cos (₀t + (t))}. (4)

Необходимо отметить, что “физический смысл” модуляции сохраняется лишь в том случае, когда модулирующий сигнал является “медленно меняющимся” по сравнению с немодулированным несущим колебанием: только при этом условии имеется возможность нестрого, “по-инженерному”, но все-таки не без смысла говорить о “синусоиде с переменной амплитудой (фазой, частотой) “. Однако удобнее все-таки говорить не о “переменной амплитуде”, а об “огибающей”, как это принято в радиотехнике.

Периодические сигналы. Сигналы называются периодическими, а временной интервал  – периодом, если

S_ = {x: x(t) = x(t+); –  < t < }. (5)

Сигналы с ограниченной энергией. О сигналах из множества

S_э = {x: x²(t) dt  K < } (6)

говорят, что их энергия ограничена величиной К. Происхождение этого наз­вания связано с тем, что если х(t) есть напряжение, то интеграл в фор­муле (6) представляет собой энергию, выделенную сигналом х(t) на еди­ничном сопротивлении. Конечно, если х(t) есть, например, глубина бо­роздки на грампластинке, то интеграл связан с энергией лишь косвенно.

Сигналы ограниченной длительности. Интервал Т называется длительностью сигнала х(t), если

S_T = {x: x(t)  0, t  T}; (7)

конечно, предполагается, что внутри этого интервала х(t) не везде обращается в нуль.

Особую роль среди сигналов с ограниченной длительностью играют импульсные сигналы, их отличие состоит в “кратковременности” Т, которую трудно формализовать, но которая проявляется в практике: звуки типа “щелчок”, “взрыв”, “хлопок”; световые “вспышки”; тактильные сигналы “укол”, “щипок”, “удар” и т.п. В таких случаях х(t) обычно называется “формой импульса”. На практике очень распростра­нены периодические последовательности импульсов (радио­ло­ка­ция, элек­трокардиография, ультразвуковая гидролокация и т.п.); не менее важны непериодические импульсные последовательности (те­ле­гра­фия, цифровая телеметрия); в реальности все импульсные последовательности, в свою очередь, имеют ограниченную длительность.

Сигналы с ограниченной полосой частот. Фурье-преобразование Х() временной реализации х(t) сигнала называется ее спектром:

Х() = x(t)e ^i2t dt. (8)

Физический смысл спектра состоит в том, что колебание х(t) представляется в виде суммы (в общем случае в виде интеграла) составляющих его гармонических колебаний с определенными амплитудами |х()|, частотами  и соответствующими фазами. Между х(t) и Х() имеется взаимно однозначное соответствие, так как

x(t) = X()e^{– i2t} dt. (9)

Условием существования и обратимости Фурье-преобразования является ограниченность энергии сигнала (интегрируемость в квадрате функций х(t) и Х()) и его непрерывность.

Если функция Х() на оси  имеет ограниченную “длительность” F (в смысле соотношения (7), но в частотной области), то говорят, что сигнал х(t) имеeт ограниченную полосу частот шириной F:

S_B = {x: Х() = x(t) e ^{i2 t} dt = 0 для всех  > |F|}. (10)

НЕКОТОРЫЕ МОДЕЛИ АНСАМБЛЯ РЕАЛИЗАЦИЙ

Нормальный шум. Удобной моделью помех и некоторых полезных сигналов является стационарный нормальный случайный процесс. Такое название вызвано тем, что случайные мгновенные значения величины х(t) предполагаются подчиненными нормальному закону (с нулевым средним), т.е. плотность распределения первого порядка выражается формулой

; (11)

для плотности распределения второго порядка справедлива формула

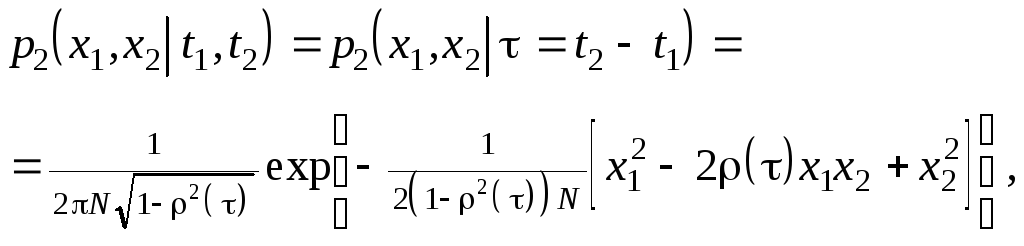₍₁₂₎

а для n-мерной плотности – формула

. (13)

Использованные здесь обозначения таковы:

N = Е(Х²) – мощность шума (дисперсия мгновенных значений);

() = N^1Е(Х_t Х_t+) – нормированная функция автокорреляции;

с_ij = Е (Х_ti Х_tj) , с_ii = N – коэффициенты ковариации; С = || с_ij ||, |С| – определитель матрицы С;

|с_ij| – алгебраическое дополнение элемента с_ij, т.е. умноженный на ( – 1)^i+j определитель матрицы (n – 1) -го порядка, полученной из С вычеркиванием i-й строки и j-го столбца.

Замечательной особенностью нормального процесса является то, что его распределение любого порядка полностью определяется только первыми двумя моментными функциями: средним (которое в формулах (11) – (13) принято равным нулю) и ковариационной функцией , так какс_ij = N (t_i – t_j) .

Сигнал как колебание со случайными огибающей и фазой. Понятия амплитуды и фазы, введенные первоначально для гармонических сигналов, с помощью модуляции были обобщены на сигналы, которые уже не являются гармоническими. Легко обобщить их на произвольные сигналы: пока чисто формально можно задать такие функции R(t) и (t), чтобы для заданной функции х(t) было выполнено равенство

Bandpass

полоса частот

REALIZATION

реализация

NARROW-BAND

узкополосный

Установив, что случайный процесс является приемлемой моделью сигналов, мы должны построить конкретные варианты этой модели – как на уровне описания отдельных реализаций, так и с помощью моделирования сразу всего ансамбля возможных реализаций. Современная теория сигналов предлагает модели обоих типов.

x(t)=R(t)cos(?₀t+?(t)), (14)

и, сравнив его с соотношениями (1) – (4), можно трактовать R(t) и (t) как “огибающую” и “фазу” колебания с частотой ₀.

Возникает вопрос: соответствуют ли эти функции чему-нибудь реальному? Оказывается, свобода выбора в задании функций R и  при определенных условиях весьма ограничена. Эти условия мы уже упоминали как “медленность” R(t) по сравнению с cos₀t и (t) по сравнению с ₀t, а в целом этот комплекс условий в силу причин (которые мы не будем обсуждать) получил название узкополосности сигнала х(t).

Очень наглядным является векторный вариант модели (14): R и  можно рассматривать как полярные координаты некоторого вектора. Тогда всякое гармоническое колебание х(t) = Scos(₀t + ), имеющее частоту ₀, изобразится как постоянный вектор с амплитудой S и углом  к направлению, принятому за ось 0х.

Если гармонический сигнал имеет частоту, отличную от ₀ (например, ₁), то в рассматриваемой системе координат соответствующий ему вектор будет вращаться с частотой ₁ – ... ₀, поскольку соs₁t = соs(₀t + (t)), (t) = (₁ – ₀)t. Негармонический сигнал изобразится как вектор, совершающий вращения или колебания (изменяется угол) и изменяющий свою длину R.

При всей простоте такая модель позволяет легко описывать различные преобразования сигналов. Например, сумма двух колебаний с частотой ₀ изобразится как сумма двух соответствующих векторов (при этом автоматически учитываются фазовые соотношения) .

Пусть, например, принимаемый сигнал является суммой полезного сигнала s(t) и шума n(t):

х(t) = s(t) + n(t). (15)

Рассмотрим случай, когда полезный сигнал есть гармоническое колебание

s(t) = S · cos₀t , (16)

а шум является нормальным с дисперсией ² и нулевым средним. Будем считать, что ₀ значительно превышает ширину полосы частот, занимаемую сигналом х(t), так что такая узкополосность обеспечивает физический смысл понятиям его огибающей и фазы (см. формулу (14)). Направив ось 0х вдоль вектора сигнала s(t), находим его координаты х = S и y = 0. Вектор шума случаен, обе его компоненты нормальны с нулевым средним и дисперсией ². Сложение векторов сигнала и шума приводит к вектору с нормальными компонентами, у одной из которых среднее равно S, а у другой – нулю:

. (17)

Поскольку существуют радиотехнические устройства, чувствительные только к огибающей или только к фазе принимаемого сигнала, имеет смысл рассмотреть их статистические свойства. Перейдем от декартовых координат (х, у) к полярным (R, ). Используя очевидные соотношения х = Rсоs, y = Rsin, dх dy = R dR d, из равенства (17) сразу получаем распределение

(18)

Легко установить, что если S = 0 (т.е. имеется только чистый шум), то

(19)

т.е. огибающая распределена по закону Рэлея, фаза – равномерно в интервале [0, 2??, R и ? независимы (так как их совместное распределение факторизовалось).

Распределения вероятностей отдельно для огибающей R и фазы ? получаются при интегрировании совместного распределения (18) по переменной, которую нужно исключить. Например, распределение огибающей имеет вид

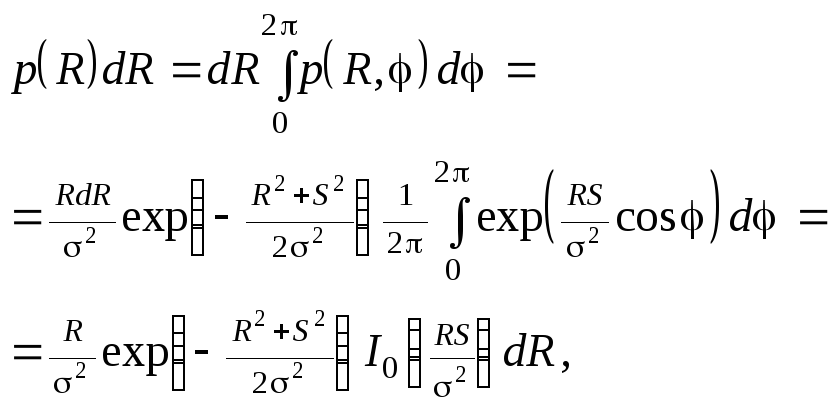(20)

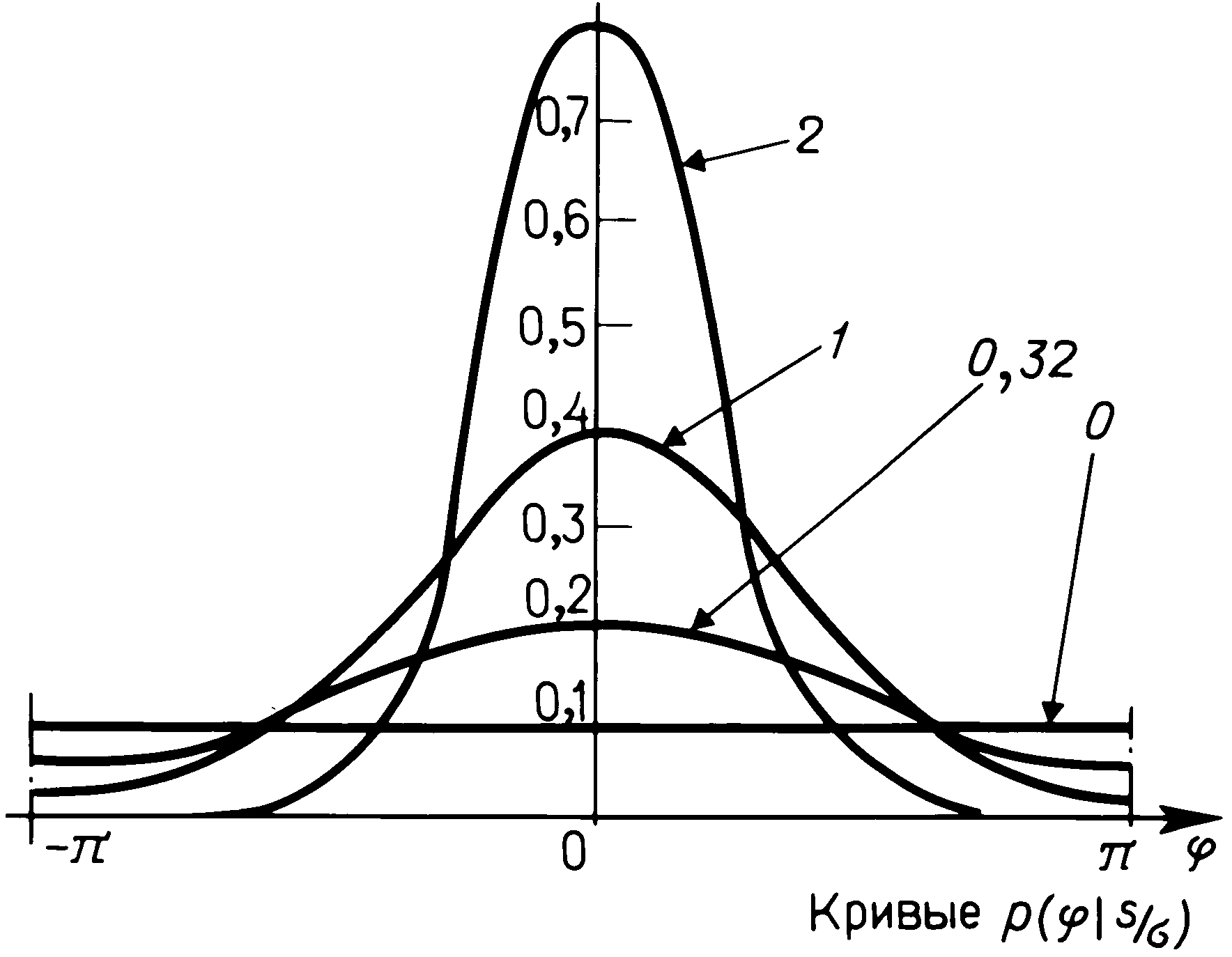
5.2 ————— График плотностей распределения вероятностей для фазы колебания, являющегося аддитивной смесью смеси синусоидального сигнала с шумом

5.1 ————— График плотностей распределения вероятностей огибающей смеси синусоидального сигнала с гауссовым шумом

где через I₀ обозначена модифицированная функция Бесселя первого рода нулевого порядка (так называется трансцендентная функция, выражаемая полученным интегралом). Это распределение называется распределением Рэля–Райса или обобщенным распределением Рэлея, поскольку при S = 0 оно обращается в обычное распределение Рэлея. Семейство кривых р(R) для различных S и ? изображено на рис. 5.1.

Распределение фазы выражается формулой

p(?)d? = d?p(R, ?)dR. (21)

Не приводя аналитических выражений для р(?) из-за их громоздкости (при необходимости см. [5]), изобразим графики этого распределения при разных S/? на рис. 5.2.

Подведем итог В данном параграфе приведено несколько наиболее употребительных моделей сигналов. Следует помнить, что в ряде случаев эти модели достаточно хорошо отображают реальные сигналы, но абсолютно точными они не бывают никогда.

Summary Several widely used models of signals have been presented in this section. It is necessary to remember that in many cases these models represent real signals well enough, but that they are never absolutely exact.