
- •Глава 1. Интерполирование
- •Постановка задачи интерполирования
- •1.2. Единственность интерполяционного многочлена
- •. Интерполяционный многочлен Лагранжа
- •1.4. Погрешность интерполяционной формулы Лагранжа
- •. Конечные разности и их свойства
- •1.6. Первая интерполяционная формула Ньютона
- •1.7. Вторая интерполяционная формула Ньютона
- •1.8. Интерполяционная формула Гаусса
- •1.10. Численное дифференцирование
- •Глава 2. Численное интегрирование
- •2.1. Общие замечания
- •Глава 3. Численные методы решения алгебраических и трансцендентных уравнений
- •3.1. Вводные замечания
- •3.2. Отделение корней
- •3.3. Метод половинного деления
- •3.5. Метод Ньютона (метод касательных)
- •3.6. Комбинированный метод
- •3.7. Метод итерации (метод последовательных приближений)
- •Глава 4. Решение систем линейных уравнений
- •4.1. Метод Гаусса (схема единственного деления)
- •4.2. Вычисление определителей
- •4.3. Вычисление обратной матрицы
- •4.4. Некоторые сведения из линейной алгебры
- •Рассмотрим систему линейных алгебраических уравнений
- •Вычитая второе равенство из первого, получаем
- •4.6. Приведение линейной системы к виду,
- •4.7. Метод Зейделя Пусть система линейных алгебраических уравнений приведена к виду
- •Глава 5. Обработка результатов наблюдений
- •5.1. Постановка задачи
- •5.2. Приближение функции, заданной таблично,
- •Глава 6. Численные методы решения
- •6.1. Методы решения задачи Коши. Вводные замечания
- •6.2. Решение дифференциальных уравнений
- •6.3. Метод Эйлера Пусть дано дифференциальное уравнение
- •6.4. Уточненный метод Эйлера Рассмотрим дифференциальное уравнение
- •6.6. Методы Рунге – Кутта Пусть дано дифференциальное уравнение
- •6.7. Метод Милна
- •6.8. Приближенное решение систем дифференциальных
- •6.9.Краевые задачи для обыкновенных дифференциальных
- •6.10. Решение краевых задач
- •6.11. Метод прогонки Рассмотрим линейную систему уравнений (6.54). Преобразуя первые (n-1) уравнения:
- •Глава 7. Численное решение дифференциальных уравнений в частных производных
- •7.1. Классификация дифференциальных уравнений
- •7.2. Метод сеток решения краевых задач
- •7.3. Погрешность аппроксимации дифференциальных уравнений
- •7.4. Аппроксимация граничных условий
- •7.6. Метод сеток для уравнений
Глава 3. Численные методы решения алгебраических и трансцендентных уравнений
3.1. Вводные замечания
Пусть задано уравнение f(x)=0, где функция f(x) определена и непрерывна на некотором конечном или бесконечном интервале. Требуется вычислить с заданной точностью действительные корни уравнения. Приближенное вычисление действительных корней уравнений производится в два этапа.
Отделение корней, т.е. нахождение достаточно малых интервалов, каждый из которых содержит один и только один корень уравнения.
Вычисление корней с заданной точностью.
3.2. Отделение корней
Для отделения корней можно использовать следующую теорему.
Теорема. Если
непрерывная функция f(x)
принимает значения разных знаков
на концах отрезка [a,b],
т.е. f(a)f(b)<0, то внутри
этого отрезка находится по крайней мере
один корень уравнения f(x)=0.
Если производная
![]() сохраняет знак на отрезке [a,b],
то корень будет единственный.
сохраняет знак на отрезке [a,b],
то корень будет единственный.
Процесс отделения
корней происходит так. Определяем знаки
функции f(x) в ряде точек
из области определения функции х1,
х2, х3,…, выбор
которых учитывает особенности функции
f(x). Если окажется, что
![]() ,
то в силу сформулированной выше теоремы
на отрезке
,
то в силу сформулированной выше теоремы
на отрезке
![]() имеется по крайней мере один корень
уравнения f(x)=0. Необходимо тем или
иным способом проверить, является ли
этот корень единственным.
имеется по крайней мере один корень
уравнения f(x)=0. Необходимо тем или
иным способом проверить, является ли
этот корень единственным.
Пример 1. Отделить действительные корни уравнения:
![]() ;
;
![]() ;
;
X |
-1 |
0 |
1 |
2 |
3 |
f(x) |
- |
- |
- |
- |
+ |
На концах отрезка
[2, 3] функция f(x) имеет
разные знаки.
![]() при всех х. Следовательно, на отрезке
[2, 3] находится единственный действительный
кореньзаданного уравнения.
при всех х. Следовательно, на отрезке
[2, 3] находится единственный действительный
кореньзаданного уравнения.
Пример 2.
![]() ;
;
![]() ;
;
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
- |
- |
+ |
+ |
- |
- |
+ |
Найдены три отрезка, содержащие корни уравнения: [-2; -1], [0; 1], [2; 3]. Так как алгебраическое уравнение третьей степени имеет три корня, каждый из отрезков содержит один корень уравнения.
Для отделения
корней можно использовать графические
методы. Действительные корни уравнения
f(x)=0 представляют собой
абсциссы точек пересечения графика
функции y=f(x) с осью 0х.
Строим график функции y=f(x) и
определяем интервалы, содержащие точки
пересечения графика с осью 0х. Иногда
удобно представить уравнение f(x)=0 в виде
![]() ,
построить графики функции
и
,
построить графики функции
и
![]() и по графику определить интервалы, в
которые попадают точки пересечения
построенных графиков.
и по графику определить интервалы, в
которые попадают точки пересечения
построенных графиков.
3.3. Метод половинного деления
Пусть дано уравнение f(x)=0 и пусть найден отрезок [a0, b0], на котором находится единственный корень уравнения. Обозначим корень уравнения через . Для нахождения корня уравнения делим отрезок [a0, b0] пополам.
Если
![]() ,
то
,
то
![]() ,
и задача решена. Если
,
и задача решена. Если
![]() ,
выбираем ту из половин отрезка [a0,
b0],
на концах которой функция f(x) имеет
противоположные знаки. Новый суженный
отрезок [a1,
b1]
снова делим пополам и повторяем те же
действия и т.д. (рис.3.1.). В результате
получаем на каком-то этапе или точный
корень уравнения, или же последовательность
вложенных друг в друга отрезков
,
выбираем ту из половин отрезка [a0,
b0],
на концах которой функция f(x) имеет
противоположные знаки. Новый суженный
отрезок [a1,
b1]
снова делим пополам и повторяем те же
действия и т.д. (рис.3.1.). В результате
получаем на каком-то этапе или точный
корень уравнения, или же последовательность
вложенных друг в друга отрезков
[a0, b0], [a1, b1], [a2, b2], …, [an, bn],
таких, что
![]() ;
(3.1)
;
(3.1)
![]() ;
(3.2)
;
(3.2)
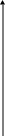 y
y





 0
а1
b1
0
а1
b1
а0 а2 b2 b0 x
Рис.3.1.
Рассмотрим
последовательность а0, а1,
а2, а3,… . Эта последовательность
имеет предел, так как она монотонно
неубывающая, ограниченная (все
![]() ).
Последовательность b0,
b1, b2, b3,…
также имеет предел, так как она
монотонно невозрастающая, ограниченная
(все
).
Последовательность b0,
b1, b2, b3,…
также имеет предел, так как она
монотонно невозрастающая, ограниченная
(все
![]() ).
).
Перейдем к пределу
при
![]() в равенстве (3.2):
в равенстве (3.2):
![]() .
.
Таким образом,
![]() .
.
Обозначим общий предел этихх последовательностей через с. перейдем к пределу при в неравенстве (3.1):
![]() .
.
Отсюда
![]() ,
т.е. с – корень уравнения f(x)=0.
Таким образом,
,
т.е. с – корень уравнения f(x)=0.
Таким образом,
![]() .
.
Если необходимо
вычислить корень уравнения с точностью
до
![]() ,
деление отрезка [a,b]
производим до тех пор, пока
,
деление отрезка [a,b]
производим до тех пор, пока
![]() .
За приближенное значение корня берем
среднюю точку отрезка
.
За приближенное значение корня берем
среднюю точку отрезка
![]() .
.
При этом
![]() .
.
метод половинного деления практически неудобен для вычисления корня с большой точностью ручным способом, так как требует большого объема вычислительной работы. Но он легко реализуется на ЭВМ.
Пример. Вычислить
с точностью до
![]() действительный корень уравнения
действительный корень уравнения
![]() .
.
Обозначим
![]() .
.
Вычисляем f(1)=3
и f(2)=6. Следовательно,
на отрезке [1, 2] находится
корень заданного уравнения, причем
единственный, так как
![]() >0
при всех х.
>0
при всех х.
Обозначим а0=1,
b0=2.
Применим метод половинного деления.
Деление производим до тех пор, пока
![]() (таблю3.1).
(таблю3.1).
Отметим,
что
![]() можно вычислить грубо, так как требуется
только знак этого значения.
можно вычислить грубо, так как требуется
только знак этого значения.
Таблица 3.1
|
|
|
|
|
|
0 1 2 3 4 |
1 1 1.25 1.375 1.4375 |
2 1.5 1.5 1.5 1.5 |
1 0.5 0.25 0.125 0.0625 |
1.5 1.25 1.375 1.4375 1.46875 |
0.37 -1.58 -0.65 -0.15 |
Ответ:
![]() .
.
3.4. Метод хорд
Дано уравнение
f(x)=0. Пусть найден отрезок
![]() такой, что на концах его функция
имеет разные знаки, т.е.
такой, что на концах его функция
имеет разные знаки, т.е.
![]() .
Пусть, кроме этого производные
.
Пусть, кроме этого производные
![]() и
и
![]() на
отрезке
сохраняют знак. Положим для определенности
на
отрезке
сохраняют знак. Положим для определенности
![]() ,
,
![]() ,
,
![]() ,
,
![]() при
при
![]() .
За приближенное значение корня принимаем
точку пересечения с осью 0х хорды,
проходящей через точки
.
За приближенное значение корня принимаем
точку пересечения с осью 0х хорды,
проходящей через точки
![]() ,
,
![]() (рис.3.2).
(рис.3.2).
у
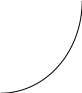


 B0
B0
а0 а1 а2 b0
y=f(x)


А0 А1
Рис. 3.2
Составим уравнение хорды:
![]() .
.
Найдем точку пересечения с осью 0х, положив у=0. Обозначим абсциссу точки пересечения хорды с осью 0х через а1:
![]() .
.
Принимая а1 за конец нового отрезка [a1,b0] , можно снова провести хорду и получить второе приближение корня а2:
![]()
и т. д.
![]() (n=0,1,2,…).
(n=0,1,2,…).
Докажем сходимость этого процесса. Рассмотрим последовательность а0, а1, а2, … .Это – монотонно возрастающая ограниченная последовательность
а0<a1<a2<…<an<…<b0
имеющая
предел. Пусть
![]() . Переходим к пределу при
в равенстве (3.3):
. Переходим к пределу при
в равенстве (3.3):
![]() .
.
Отсюда f(c)=0
, т.е. с – корень уравнения. Так как
на отрезке [a0,b0]
корень единственный , получаем
![]() .
.
Таким образом ,
последовательность а0 ,а1,
а2,… сходится и в пределе дает
корень уравнения
![]() .
.
Аналогично показывается сходимость для остальных случаев.
