6.7. Метод Милна

Рассмотрим дифференциальное уравнение

с начальным условием

.

Выбрав шаг h, положим . Предположим, что нам удалось каким-либо образом найти приближенное решение в точках . Покажем, как по этим четырем значениям можно найти приближенное значение решения дифференциального уравнения в точке x_n+1.

Проинтегрируем обе части дифференциального уравнения от х_n-3 до х_n+1:

.

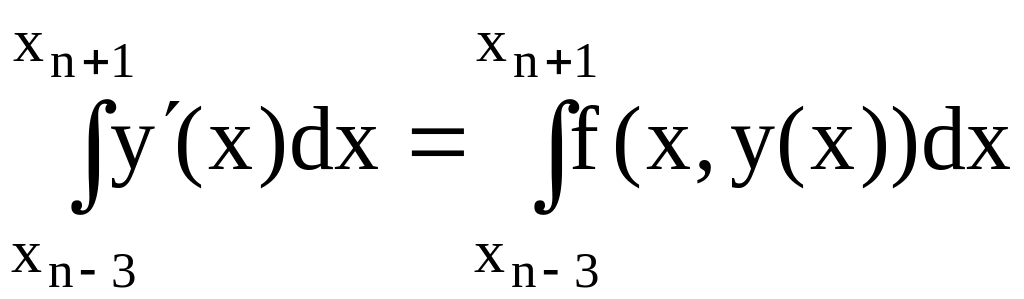Отсюда

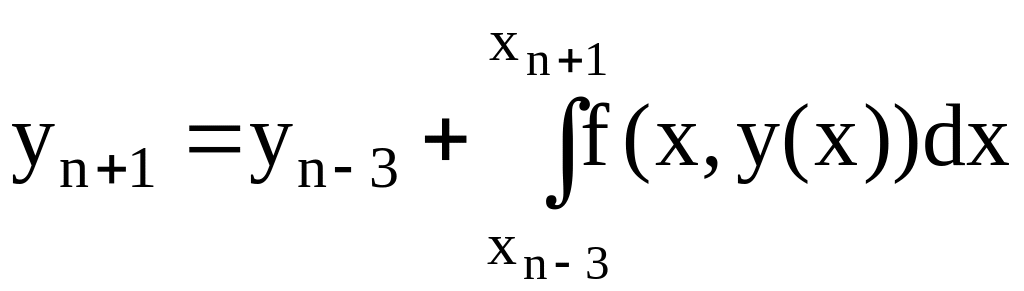(6.32)

Для подынтегральной функции f(x,y(x)) построим интерполяционный многочлен третьей степени на отрезке по узлам . Воспользуемся первой интерполяционной формулой Ньютона

,

где

.

Подставляя интерполяционный многочлен вместо функции f в (6.32), приближенно получаем

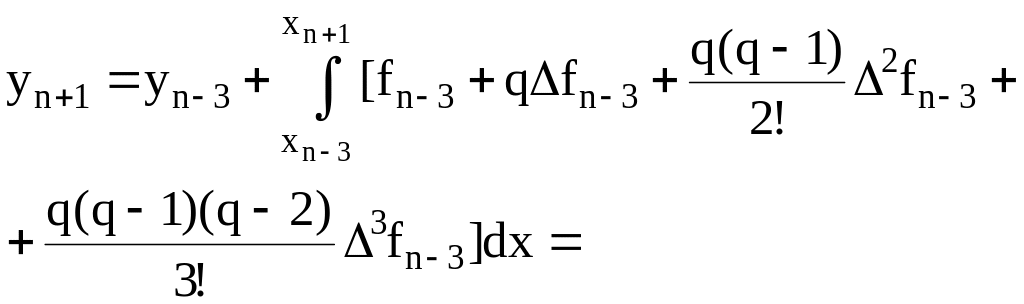
= , dx=hdq;

q=0 при x=x_n-3; =

q=4 при x=x_n+1.

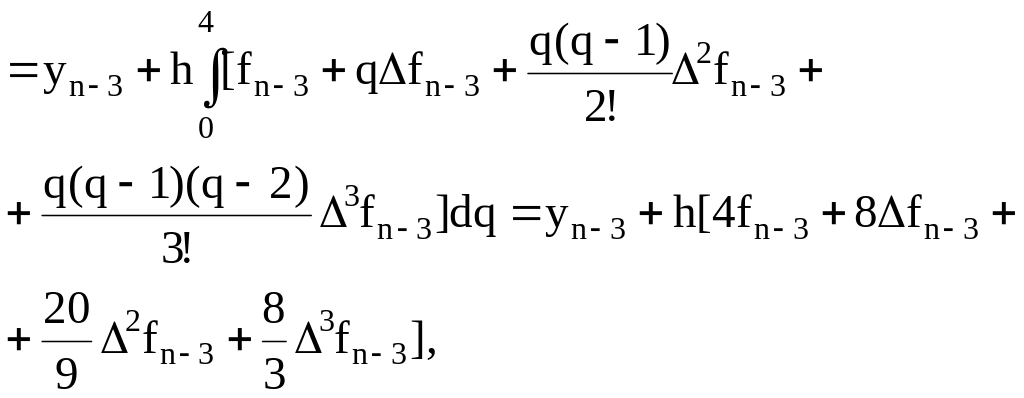(6.33)

Преобразуем полученную формулу.

Выразим конечные разности через значения функции:

Подставляя полученные выражения для конечных разностей в формулу (6.33), получаем первую формулу Милна

. (6.34)

Для вывода второй формулы Милна интегрируем обе части исходного дифференциального уравнения от x_n-1 до x_n+1:

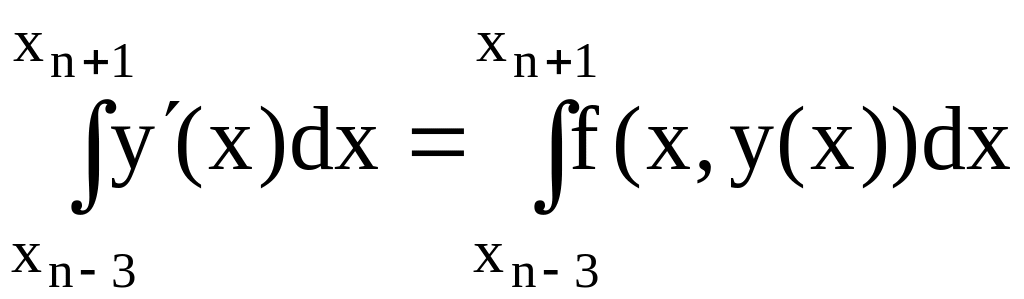
Отсюда

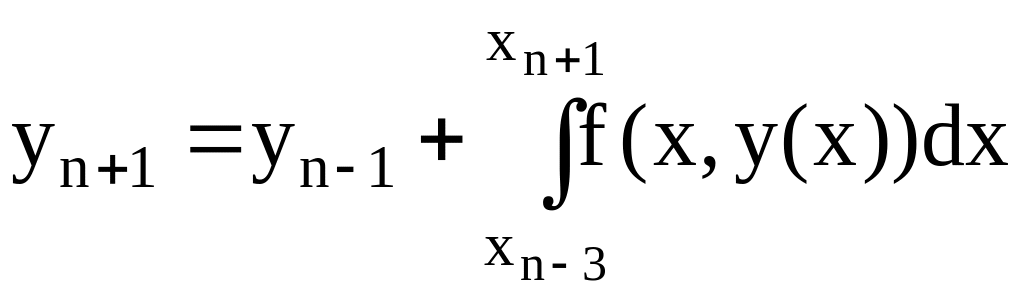(6.35)

Для подынтеральной функции f(x,y(x)) построим интерполяционный многочлен третьей степени на отрезке . Воспользуемся первой интерполяционной формулой Ньютона

,

где

.

Подставляя интерполяционный многочлен вместо функции f в (6.35) приближенно получаем

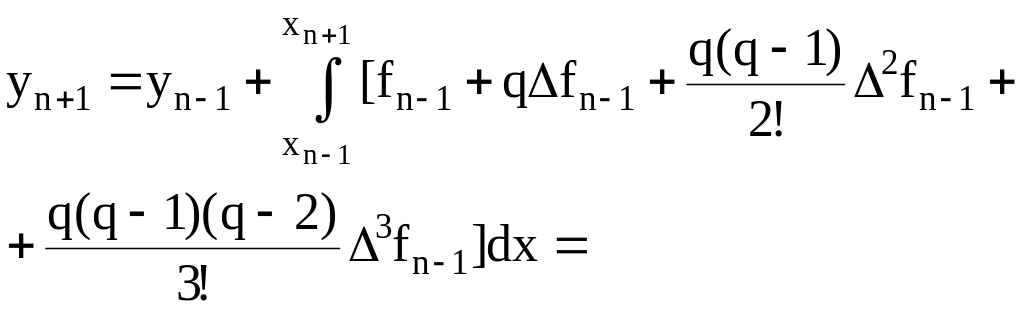
= , dx=hdq;

q=0 при x=x_n-1; =

q=2 при x=x_n+1.

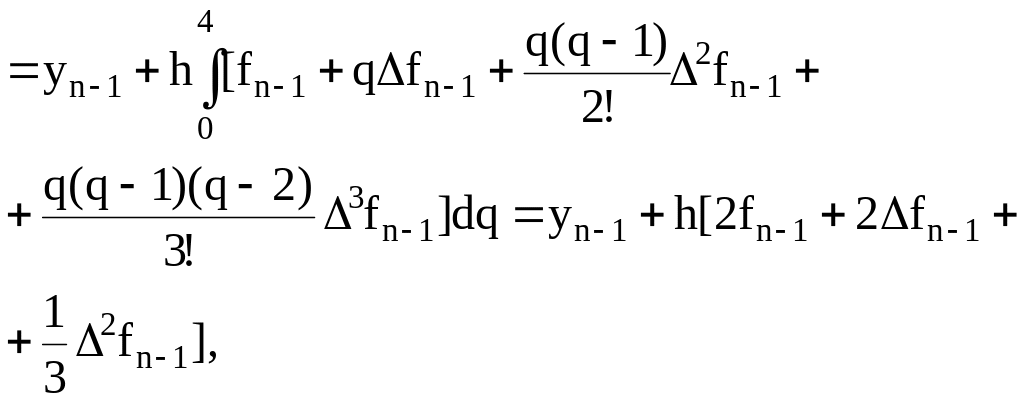(6.36)

Преобразуем полученную формулу. Выразим конечные разности через значения функции:

.

Подставляя полученные выражения для конечных разностей в формулу (6.36), получим вторую формулу Милна

. (6.37)

Обозначим:

- значение у_к, найденные по первой формуле Милна;

.

Метод Милна применяется следующим образом.

1. Вычисляем первое приближение по первой формуле Милна:

.

2. По значению вычисляем

.

3. Находим второе приближение у_n+1 по второй формуле Милна:

.

Первая формула Милна служит «предсказывающей» формулой (формулой прогноза), вторая – «поправочной» формулой (формулой корректировки). Методы, в которых сначала находится предварительное значение функции по одной формуле, а затем это значение уточняется по другой формуле, объединяются под общим названием методов прогноза и коррекции.

Метод Милна, как видно из рассмотренного выше, - многошаговый метод. Для применения метода Милна необходимо найти первые четыре значения решения дифференциального уравнения: у₀, у₁, у₂, у₃, используя начальное условие и какой-либо метод, например, метод Рунге – Кутта.

Оценим погрешность метода Милна. Так же, как и для экстраполяционного метода Адамса, погрешность метода Милна на одном шаге есть величина порядка h^s.

На практике для оценки погрешности метода Милна ограничились разностями третьего порядка. Обозначим - погрешности первой и второй формул Милна соответственно. Учитывая отброшенные в интерполяционной формуле Ньютона разности четвертого порядка, с точностью до разностей пятого порядка будем иметь:

.

Отсюда, считая, что четвертые разности практически постоянны на отрезке длины 4h, получим

.

Так как

,

получаем

.

Отсюда

. (6.38)