1.10. Численное дифференцирование

Пусть функция f(x) задана таблицей своих значений на отрезке [a,b]. Требуется вычислить производную порядка m в некоторой точке х отрезка [a,b]. Задача эта может быть решена следующим образом. По заданным узлам интерполяции строим интерполяционный многочлен . Тогда

, (1.42)

где - погрешность интерполирования.

Дифференцируем тождество (1.42) m раз в предположении, что f(x) имеет производную порядка m, и получаем

.

Пренебрегая величиной , получим формулу для приближенного вычисления производной:

. (1.43)

Погрешность этой формулы равна .

Отметим, что численное дифференцирование – операция менее точная, чем интерполирование.

Интерполяционный многочлен может быть построен по любой из рассмотренных ранее формул. Рассмотрим подробнее случай равноотстоящих узлов. Пусть . Предположим для определенности, что точка х, в которой требуется вычислить производную, лежит в начале таблицы. Воспользуемся первой интерполяционной формулой Ньютона

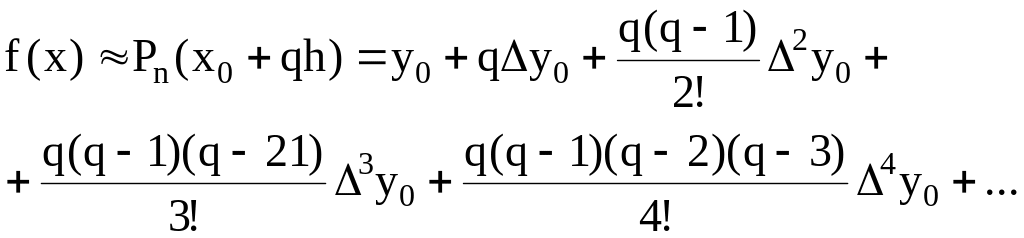, (1.44)

где .

Дифференцируем (1.44) по переменной х. Отметим, что

.

После дифференцирования получаем

. (1.45)

Аналогично находим

(1.46)

Таким же способом в случае надобности можно вычислить и производные функции f(x) ,более высокого порядка. Если точка х лежит в середине или в конце таблицы, формулы для вычисления производных получим из интерполяционной формулы Гаусса или второй интерполяционной формулы Ньютона соответственно. Формулы численного дифференцировния упрощаются, если требуется вычислить производные в узлах интерполяции. Пусть х=х₀ . Тогда q=0. Формулы (1.45) и(1.46) запишутся в виде

;

.

Погрешность в вычислении первой производной в точке х₀ равна

.

Аналогично может быть найдена погрешность для второй производной.

Глава 2. Численное интегрирование

2.1. Общие замечания

Если функция f(x) непрерывна на отрезке [a,b], то определенный интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона – Лейбница

,

где F(x) – первообразная функция f(x).

На практике, как уже указывалось во введении, часто встречаются функции, для которых первообразная не выражается через элементарные функции, а также функции, заданные таблично. вСе это приводит к необходимости применения численных методов. Для получения формул приближенного вычисления интеграла подынтегральную функцию на отрезке [a,b] заменяют интерполирующей функцией (чаще всего интерполяционным многочленом)

.

Тогда

= + .

Отбрасывая второе слагаемое полученного соотношения, приближенно полагаем

. (2.1)

Погрешность равенства (2.1) равна , где - погрешность интерполирования.

Интерполяционный многочлен может быть записан в различных видах в зависимости от применяемой интерполяционной формулы и степени m. После подстановки в (2.1) получаем различные формулы для приближенного вычисления определенного интеграла, которые называются квадратурными формулами.

2.2. Формула трапеций

Заменим подынтегральную функцию интерполяционным многочленом первой степени, построенным по двум узлам интерполяции и . Значения подынтегральной функции в узлах интерполяции равны соответственно и

.

Подставляем в (2.1):

.

Итак,

. (2.2)

Получена формула трапеций. Геометрический смысл формулы (2.2) отображен на рис. 2.1.

y=f(x)

B

у

y=h(x)

A

0 a b x

Рис. 2.1

Левая часть формулы – площадь криволинейной трапеции, правая часть – площадь трапеции аАВb.

Оценим погрешность формулы трапеций. Предположим, что f’’(x) непрерывна на отрезке [a,b]. Имеем

= , (2.3)

где .

К полученному интегралу применим обобщенную теорему о среднем, которая формулируется следующим образом.

Пусть функция непрерывна, а функция q(x) интегрируема на отрезке [a,b]. Пусть, кроме этого, (или ) для . Тогда найдется точка , такая, что

.

Подынтегральная функция интеграла (2.3) представляет собой произведение двух функций: одна функция непрерывна, а на отрезке . После применения обобщенной теоремы о среднем получаем

, (2.4)

где .

Погрешность R пропорциональна (b-a)³, поэтому, если длина отрезка большая, погрешность формулы трапеции также большая. Для увеличения точности формулы трапеций разделим отрезок на n равных частей длины .

Точки деления , , …, .

Применим формулу трапеций (2.2) к каждому отрезку :

. (2.5)

Погрешность этой формулы равна

,

где .

Сумма интегралов (2.5) по всем отрезкам дает общую квадратурную формулу трапеции

. (2.6)

Погрешность этой формулы

.

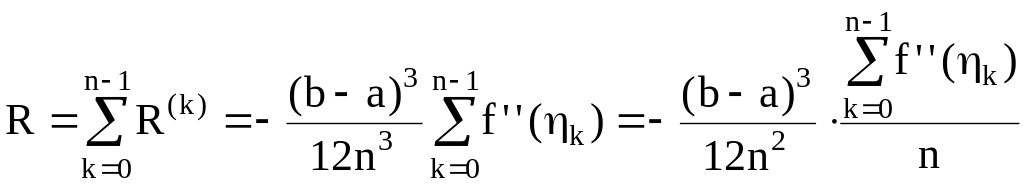Величина есть среднее арифметическое, составленное из n значений второй производной; оно лежит где-то между этими значениями. Вторую производную мы предполагали непрерывной на отрезке [a,b], поэтому она принимает все промежуточные значения. Отсюда вытекает, что на отрезке [a,b] найдется такая точка , что

и

(2.7)

Формула трапеций является точной, если подынтегральная функция – многочлен степени, не выше первой.

2.3.Формула Симпсона

Заменим подынтегральную функцию интерполяционным многочленом второй степени, построенным по трем узлам интерполяции:

, , ;

.

Интерполяционный многочлен запишем при помощи первой интерполяционной формулы Ньютона

,

где

; ;

=

= . (2.8)

Полученная формула называется формулой парабол, или формулой Симпсона (Т. Симпсон (1710 – 1761) – английский математик).

Эта формула является точной для любого многочлена второй степени (погрешность интерполирования в этом случае равна нулю). Кроме того, формула Симпсона является точной для (левая и правая части формулы (2.8) обращаются в этом случае в нуль). Отсюда вытекает, что формула Симпсона является точной для любого многочлена третьей степени. Погрешность формулы Симпсона для произвольной подынтегральной функции записывается в следующем виде:

. (2.9)

Предполагается, что непрерывна на [a,b]. Для увеличения точности формулы Симпсона (2.8) разделим отрезок [a,b] на n равных частей длины , причем возьмем n четное, т.е. n=2m. Рассмотрим сдвоенный частичный отрезок и применим к нему формулу Симпсона (2.8):

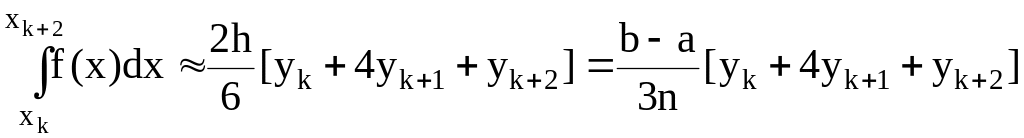(2.10)

Погрешность этой формулы, согласно (2.9) равна

= . (2.11)

Всего сдвоенных частичных отрезков .

Сумма интегралов (2.10) по всем сдвоенным отрезкам дает общую формулу Симпсона

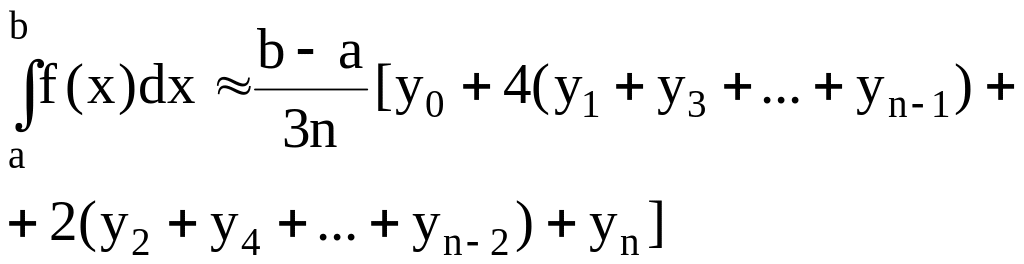. (2.12)

Погрешность этой формулы

= .

В силу непрерывности на отрезке [a,b] на этом отрезке существует такая точка , что

= .

Следовательно, имеем

(2.13)

2.4.Оценка погрешности квадратурных формул

Если подынтегральная функция f(x) задана аналитически и нахождение (для формулы трапеций) или (для формулы Симпсона) не вызывает затруднений, погрешность квадратурной формулы вычисляется по формуле (2.7) или (2.13). но на практике найти и оценить, например, производную четвертого порядка трудно, особенно в тех случаях, когда функция f(x) задана таблично. Поэтому часто прибегают к следующему приему грубой оценки погрешности, предложенному Рунге. Погрешность формулы трапеций может быть записана в виде

Обозначим

; .

Тогда ;

.

Объединяя эти результаты, можно записать, что погрешность квадратурной формулы

,

где k, N – постоянные;

h – длина частичного отрезка при разбиении отрезка [a,b] на n равных частей.

Обозначим : I – точное значение интеграла, I_h – приближенное его значение, вычисленное по квадратурной формуле с шагом h.

Тогда

. (2.14)

Вычислим этот же интеграл по квадратурной формуле с шагом 2h:

. (2.15)

Отметим, что вычисление затруднений не вызывает, так как не требуется вычисления новых значений подынтегральной функции.

Приравниваем правые части равенств (2.14) и (2.15):

.

Отсюда

;

Итак, погрешность квадратурной формулы при вычислении интеграла с шагом h удовлетворяет неравенству

.

Для формулы трапеций к=2, отсюда

. (2.16)

Для формулы Симпсона к=4, отсюда

. (2.17)

Пример. Вычислить приближенно интеграл по формуле трапеций и по формуле Симпсона при n=8. Оценить погрешность. Вычисления оформить в виде табл. 2.1.

Таблица 2.1

			Формула трапеций		Формула Симпсона
0 1 2 3 4 5 6 7 8	0 0.125 0.250 0.375 0.500 0.625 0.750 0.875 1	1 1.000244 1.003906 1.019775 1.062500 1.152588 1.316406 1.586182 2	1 2 2 2 2 2 2 2 1	1 0 2 0 2 0 2 0 1	1 4 2 4 2 4 2 4 1	1 0 4 0 2 0 4 0 1
			19.283202	9.765624	28.800780	14.406248
I			Ih=1.2052 00	I2h=1.22 0703	Ih=1.2000 32	I2h=1.200 520

Рассмотрим, как заполняются столбцы, соответствующие вычислению интеграла по формуле трапеций

.

В нашем случае

А=0, b=1, n=8;

. (2.18)

В столбце с_к проставлены коэффициенты суммы (2.18). в строке записано значение . В строке I записан ответ I_h .

Для оценки погрешности вычисляем I_2h

.

Так как точки х₁, х₃, х₅, х₇ пропускаются, полагаем для них . Аналогично ведем вычисления по формуле Симпсона. Оценим погрешности:

;

.

Итак,

(по формуле трапеций);

(по формуле Симпсона).

Отметим, что точное значение интеграла равно 1.2.