6.4. Уточненный метод Эйлера Рассмотрим дифференциальное уравнение

с начальным условием

.

Выбрав шаг h, положим .

Уточненный метод Эйлера заключается в следующем. Сначала вычисляем вспомогательное значение искомой функции в точке (6.14)

затем находим значение правой части дифференциального уравнения (6.1) в средней точке :

(6.15)

и, наконец, полагаем

. (6.16)

Таким образом, на каждом частичном отрезке [x_n, x_n+], (n=0,1,2,…) интегральную кривую заменяем отрезком прямой, проходящей через точку (x_n, x_n+1) и имеющей угловой коэффициент . Уточненный метод Эйлера - одношаговый метод. Оценим погрешность уточненного метода Эйлера на одном шаге. Согласно формуле (6.16)

=

. (6.17)

Воспользуемся формулой Тейлора для функции двух переменных

,

где - величина порядка . После применения формулы Тейлора равенство (6.17) запишется в следующем виде:

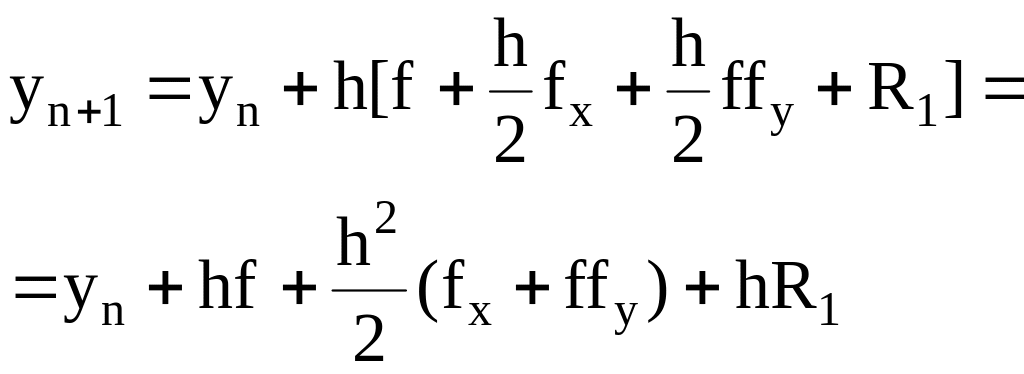, (6.18)

где значения функции f(x,y) и ее производных вычисляются при у=у_n, х=х_n. Остаточный член есть величина порядка h², и, следовательно, есть величина порядка h³.

Сравниваем (6.12) и (6.18). Отсюда вытекает, что найденное при помощи уточненного метода Эйлера приближенное решение совпадает с разложением в ряд Тейлора вплоть до членов порядка h². Погрешность уточненного метода Эйлера на одном шаге есть величина порядка h³.

6.6. Методы Рунге – Кутта Пусть дано дифференциальное уравнение

с начальным условием

.

Выбрав шаг h, положим . Приближенное решение заданного уравнения может быть полученно при помощи методов Рунге – Кутта, к которым относятся методы, обладающие следующими свойствами:

1. Эти методы являются одношаговыми.

2. Приближенные решения, найденные при помощи этих методов, совпадают с рядом Тейлора вплоть до членов порядка h^р, где степень р различна для различных методов и называется порядком метода.

3. Эти методы не требуют вычисления производных от правой части дифференциального уравнения f(x,y), а требуют только вычисления самой функции.

Отметим, что для продвижения на один шаг (т.е. для вычисления у_n+1 по предыдущей точке (x_n,y_n) функцию f(x,y) придется вычислять в нескольких вспомогательных точках отрезка [x_n, x_n+1]. Однако это намного удобнее, чем вычислять значения производных.

Очевидно, что метод Эйлера, рассмотренный в параграфе 6.3, является одним из методов Рунге – Кутта первого порядка. Для продвижения на один шаг при помощи метода Эйлера требуется вычислить (см.(6.13)). Уточненный метод Эйлера, рассмотренный в пункте 6.4, является одним из методов Рунге – Кутта второго порядка. Для продвижения на один шаг при помощи уточненного метода Эйлера необходимо вычислить и (см. (6.14) – (6.16)).

Одним из самых употребительных на практике численных методов решения дифференциальных уравнений является метод Рунге – Кутта четвертого порядка, который заключается в следующем. Последовательно вычисляем четыре числа по формулам:

(6.19)

Полагаем

. (6.20)

Выбор постоянных производим так, чтобы разложения (6.12) и (6.20) по степеням h совпадали до возможно более высоких степеней h при произвольной функции f(x,y) и произвольном шаге h (при разложении по степеням h используют формулу Тейлора для функции двух переменных).

Доказано, что при

(6.21)

разложения (6.12) и (6.20) по степеням h совпадают до членов порядка h⁴ включительно.

С учетом (6.21) формула (6.20) запишется в виде

, (6.22)

где вычисляются по формулам (6.19).

Таким образом, для продвижения на один шаг из точки необходимо по формулам (6.19) вычислить и по формуле (6.22) - .

Погрешность метода на одном шаге есть величина порядка h^s.

Рассмотренный метод, как уже указывалось, является методом Рунге – Кутта четвертого порядка. Этот метод применяется настолько широко, что в литературе он часто называется методом Рунге – Кутта без указаний на порядок.

Вычисления по методу Рунге – Кутта, необходимые для получения у₁ по известному у₀, занесены в табл. 6.1.

Таблица 6.1

n	x	y	k=hf(x,y)	yn
0	x0	y0	k1(0)	y0=1/6(k1(0)+2 k2(0)+2 k3(0)+ k4(0))
	x0+h/2	y0+ k1(0)/2	k2(0)
	x0+h/2	y0+ k2(0)/2	k3(0)
	x0+h	y0+ k3(0)	k4(0)
	x1=x0+h	y1= y0+y0

Дальнейшие вычисления продолжаем в таком же порядке. Отметим, что шаг расчета можно менять при переходе от одной точки к другой. Для контроля правильности выбора шага рекомендуется вычислить дробь

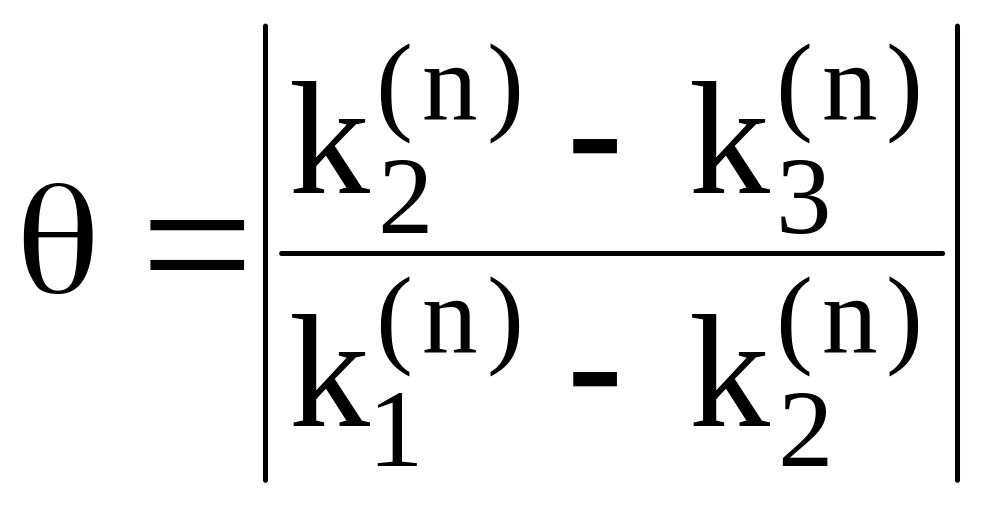. (6.23)

Величина не должна превышать нескольких сотых. В противном случае шаг h следует уменьшить.

Пример. Дано дифференциальное уравнение

с начальным условием у(1)=1.

При помощи метода Рунге – Кутта вычислить у(1,1). Шаг h принять равным 0,1. Вычисления занести в табл. 6.2.

Таблица 6.2

n	x	y	k=hf(x, y)
0	1	1	0.2	0,209999
	1,05	1,1	0,20975
	1,05	1,104875	0,210237
	1,1	1,210237	0,220024
	1,1	1,209999

Итак, .

Функция у=х² является решением рассматриваемого уравнения. Таким образом, при х=1,1 точное значение решения следующее:

у(1,1)=1,21.

6.6. Экстраполяционный метод Адамса

Недостатком метода Рунге – Кутта является то, что для получения одного нового значения решения дифференциального уравнения правую часть уравнения приходится подсчитывать в нескольких точках. Если правая часть сложна, то требуется большой объем вычислительной работы. Рассмотрим многошаговые методы, применение которых на одном шаге не требует большого объема вычислительной работы. Пусть требуется найти решение дифференциального уравнения

с начальным условием

.

Предположим, что нам удалось каким-либо образом найти приближенное решение в точках . Обозначим

.

Большое количество различных формул численного решения заданного дифференциального уравнения можно получить следующим образом. Проинтегрируем обе части дифференциального уравнения от (i – любое целое число от 0 до m ) до . Получим

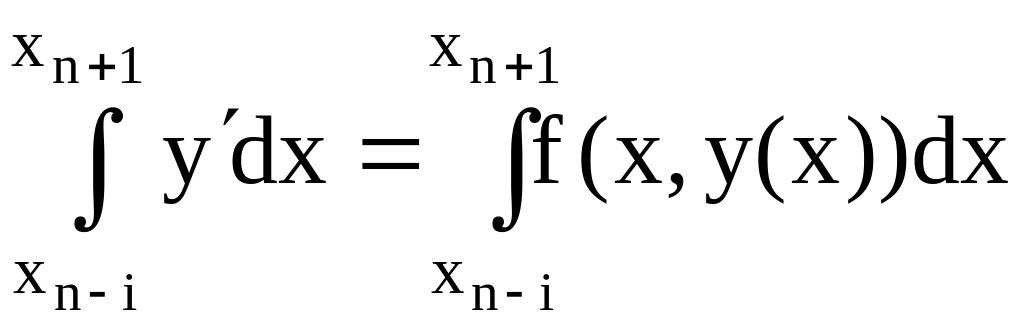
или

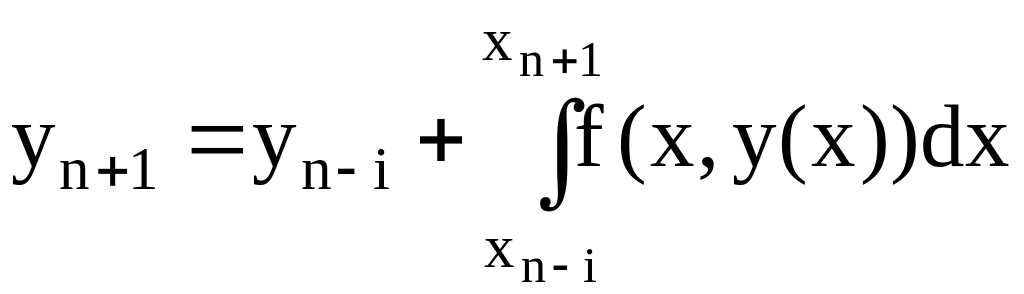(6.24)

Значения подынтегральной функции можно вычислить в (m+1)-й точке ( ). По вычисленным значениям строим интерполяционный многочлен степени m. Подставляя интерполяционный многочлен вместо f(x,y(x)) в (6.24), приближенно получим

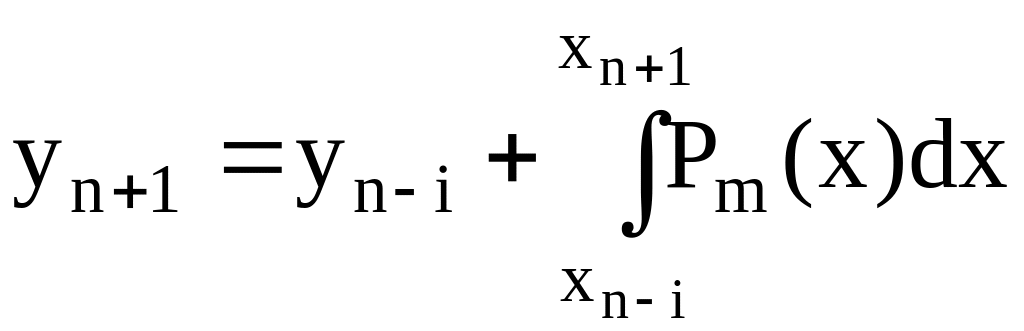(6.25)

Выбирая различные значения m, i и различные формы записи интерполяционного многочлена , получим различные формулы численного решения дифференциального уравнения.

Пусть i=0, т.е. нижний предел интегрирования в формуле (6.25) равен х_n. Равенство (6.25) запишется в виде

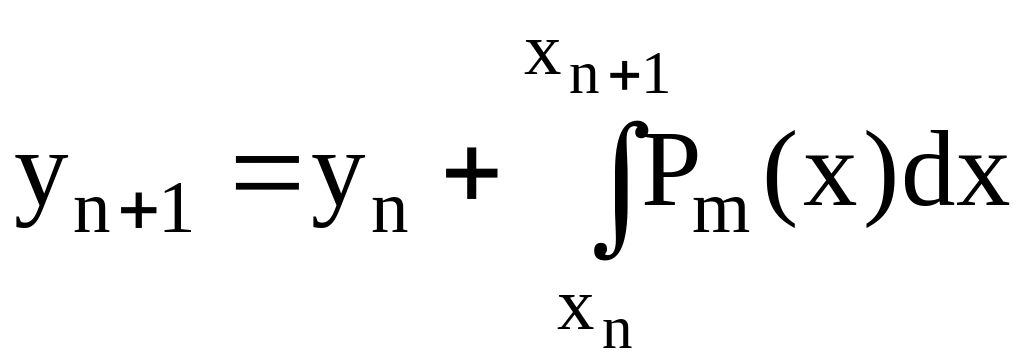. (6.26)

Для записи интерполяционного многочлена воспользуемся второй интерполяционной формулой Ньютона

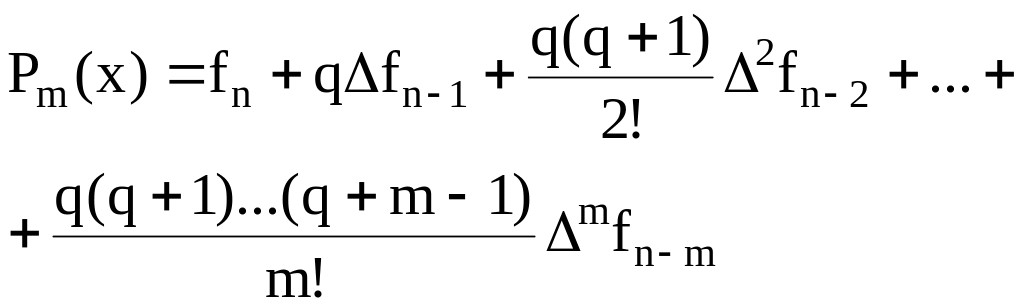, (6.27)

где .

Подставляем (6.27) в (6.26):

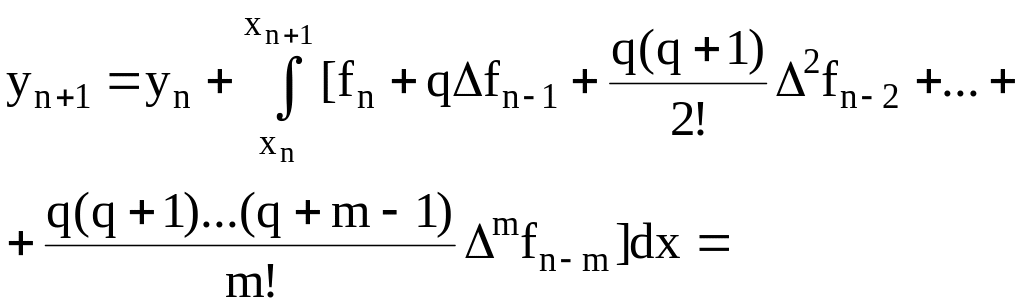
, dx=hdq;

= q=0 при x=x_n; =

q=1 при x=x_n+1.

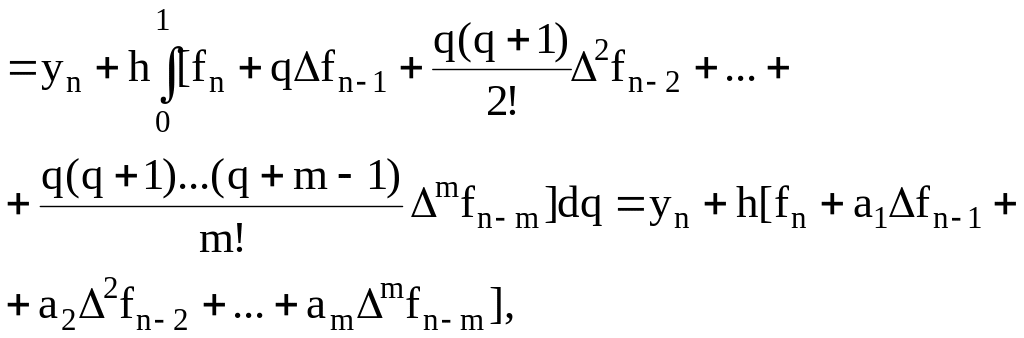
где

и т.д.

Таким образом

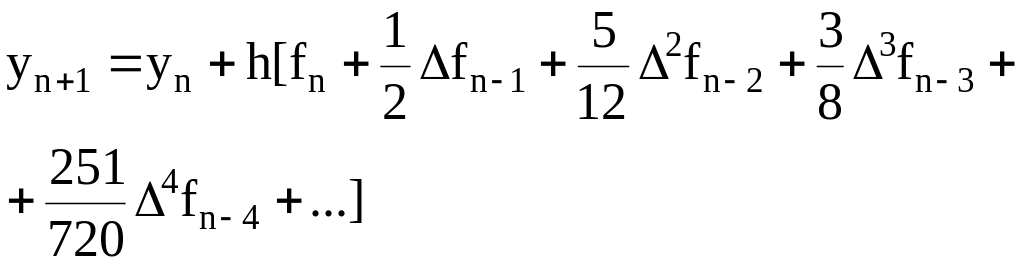(6.28)

Эта формула называется экстраполяционной формулой Адамса (Дж. Адамс (1819 – 1892) – английский астроном, математик и механик) в связи с тем, что интерполяционный многочлен используется вне отрезка, содержащего узлы интерполяции.

В вычислительной практике чаще всего используется экстраполяционная формула Адамса при m=3, т.е. подынтегральная функция f(x,y(x)) в формуле (6.24) заменяется интерполяционным многочленом третьей степени. При построении интерполяционного многочлена используются четыре значения приближенного решения: y_n-3, y_n-2, y_n-1, y_n.

Экстраполяционная формула Адамса в этом случае имеет следующий вид:

(6.29)

Для начала вычислений по формуле (6.29) нужны четыре значения:

у₀, y₁, y₂, у₃. Значение у₀ задается начальным условием. Значения y₁, y₂, у₃ вычисляются каким-либо другим методом, например методом Рунге – Кутта.

Для применения формулы (6.29) необходимо составить таблицу конечных разностей функции f. При работе на ЭВМ оперирование таблицами конечных разностей вызывает затруднения. Преобразем формулу (6.29). конечные разности , , можно выразить через табличные значения функции f, а именно:

(6.30)

Подставляя (6.30) в (6.29), получаем экстраполяционную формулу Адамса в следующем виде:

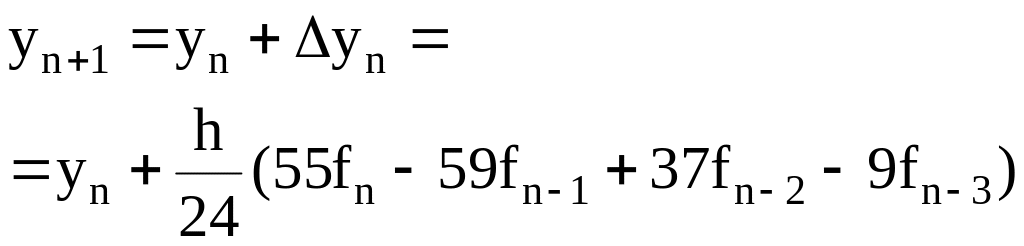. (6.31)

Оценим погрешность экстраполяционного метода Адамса (см. (6.29) и (6.31) на одном шаге. Для получения расчетных формул (6.29) и (6.31) использован интерполяционный многочлен третьей степени.

Следовательно, погрешность формул (6.29) и(6.31) можно записать в виде

.

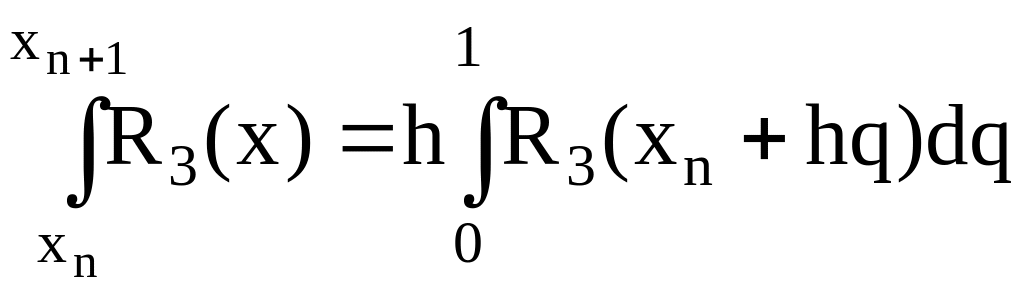Величина как погрешность второй интерполяционной формулы Ньютона пропорциональна h⁴. Следовательно, погрешность экстраполяционного метода Адамса на одном шаге есть величина порядка h⁵.