6.11. Метод прогонки Рассмотрим линейную систему уравнений (6.54). Преобразуя первые (n-1) уравнения:

или

.

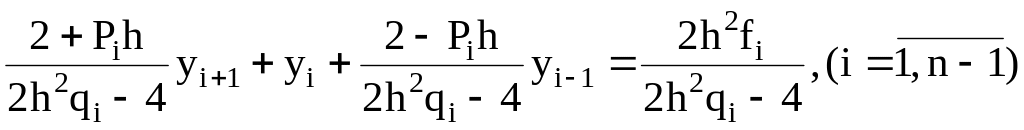Отсюда

, (6.55)

где

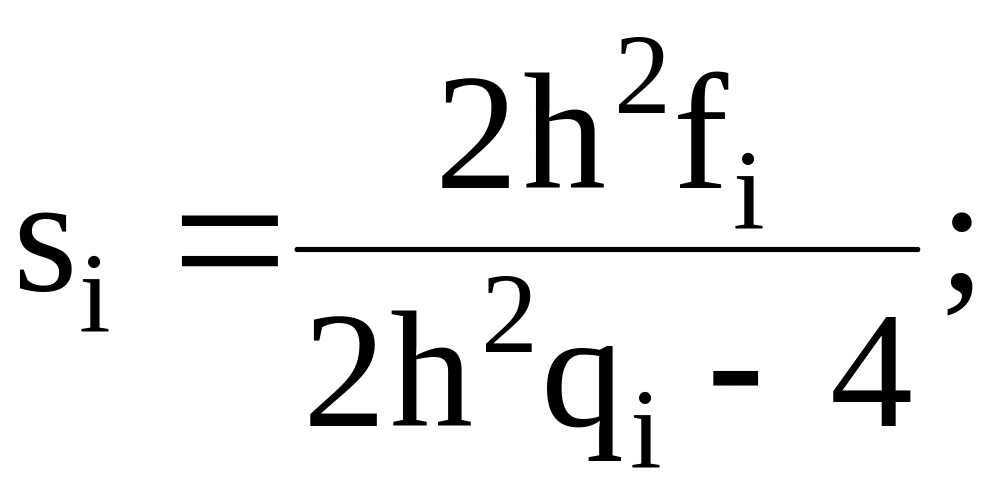
(6.56)

Предположим, что с помощью полной системы (6.55) из i-го уравнения системы исключен член, содержащий . Тогда это уравнение можно записать в виде

(6.57)

Аналогично

.

Подставляя выражение для в i-е уравнение системы (6.55), получим

.

Отсюда

. (6.58)

Сравнивая (6.57) с (6.58), получим

. (6.59)

Получены рекуррентные соотношения для определения и . Для начала подсчетов необходимо знать и . Рассмотрим систему уравнений:

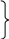(получено из (6.55) при i=1);

(получено из первого краевого условия).

Находим у₀ из второго уравнения системы:

(6.60)

и, подставляя его в первое уравнение системы, получаем

.

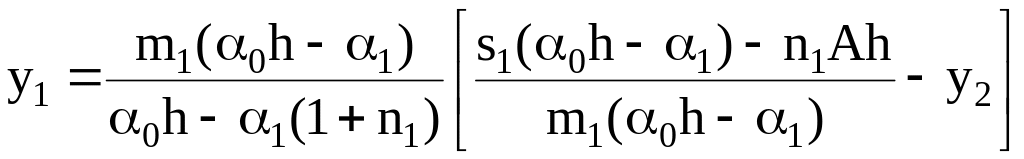Сравнивая полученное выражение с выражением

,

получаем

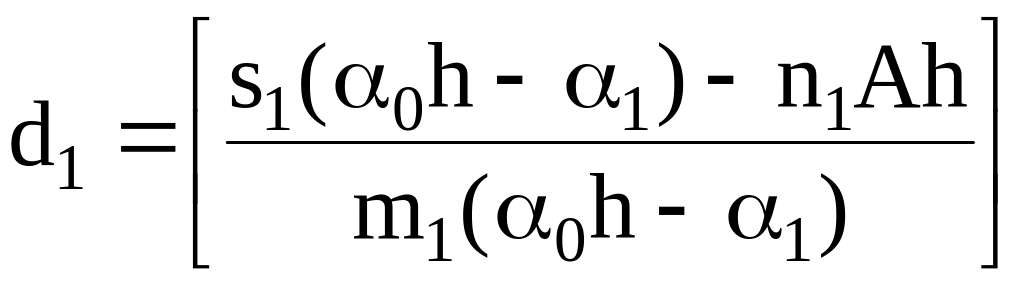; (6.61)

Итак, зная и , по формулам (6.59) можно последовательно вычислить коэффициенты и для . Вычисление коэффициентов и называется прямым ходом.

О пределим y_n из системы уравнений:

( получено из (6.57) при i=n-1);

(получено из второго краевого условия);

. (6.62)

Теперь, используя формулы (6.57) и (6.60), последовательно находим:

, , …, ;

……………………………

.

Вычисление y_i называется обратным ходом.

Вычисления удобно оформить в виде табл. 6.4.

Таблица 6.4

					Прямой ход		Обратный ход
0
1
…	…	…	…	…	…	…	…
n-1
n

Глава 7. Численное решение дифференциальных уравнений в частных производных

7.1. Классификация дифференциальных уравнений

в частных производных

Дифференциальные уравнения в частных производных имеют широкое применение в различных областях науки и техники. Получить их решение в явном виде удается только в самых простейших случаях. В связи с этим важное значение приобретают приближенные методы решения различных задач для дифференциальных уравнений в частных производных. На практике чаще всего используются линейные дифференциальные уравнения второго порядка.

Пусть D – некоторая область изменения независимых переменных х и у, ограниченная контуром Г. в области задано линейное дифференциальное уравнение второго порядка для функции U(x, y), если для любой точки из области D имеет место соотношение

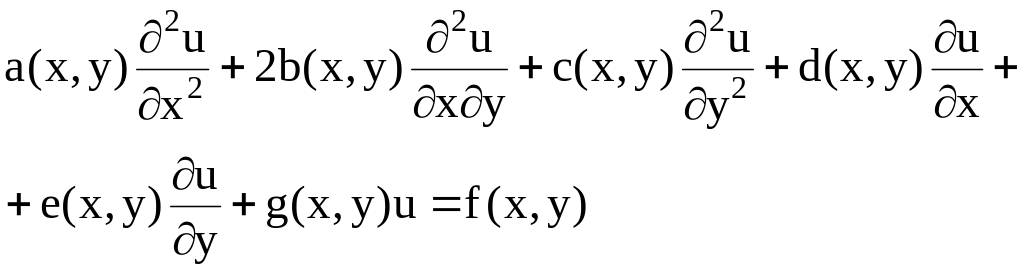. (7.1)

где - коэффициенты;

f(x,y) – свободный член уравнения.

Если коэффициенты a, b, c, d, e, g не зависят от х и у, то уравнение (7.1) является линейным дифференциальным уравнением с постоянными коэффициентами.

Обозначим

.

В зависимости от знака функции линейное дифференциальное уравнение (7.1) относится в данной области D к одному из следующих типов:

К эллиптическому - <0;

К параболическому - =0;

К гиперболическому - >0.

В дальнейших параграфах будут рассмотрены примеры каждого из трех типов уравнений и методы их приближенного решения.