7.6. Метод сеток для уравнений

параболического типа

Рассмотрим уравнение теплопроводности

, (7.15)

где u=u(x, t) – температура, t – время.

Путем введения новой переменной уравнение (7.15) приводится к виду

,

поэтому в дальнейшем полагаем а=1. Итак, рассматриваем уравнение

(7.16)

Требуется найти решение уравнения (7.16), удовлетворяющее начальному условию

(7.17)

и граничным условиям

;

. (7.18)

Рассматриваемая задача называется смешанной задачей. Решаем задачу методом сеток. Для этого рассмотрим пространственно – временную систему координат {x, t} (рис. 7.5).

t

0 B x

Рис. 7.5

Построим в полуполосе два семейства параллельных прямых:

шаг вдоль оси 0х);

шаг вдоль оси 0t).

Обозначим . Узлы имеют координаты (x_i, t_k). Узлы, лежащие на прямых х=0 и х=b, t=0, будем считать граничными узлами, все остальные – внутренними. Рассмотрим дифференциальное уравнение (7.18) во внутренних узлах. Частные производные, входящие в уравнение, заменяем конечно – разностными отношениями по формулам:

;

. (7.19)

Для внутреннего узла получаем прибилженное равенство

(7.20)

Обозначим . Тогда конечно – разностные уравнения (7.20)

Запишутся в виде

. (7.21)

Значения для граничных узлов вычисляем из условий (7.17) и (7.18):

; (7.22)

. (к=0, 1, 2, …) (7.23)

Из рассмотрения формулы (7.21) ясно, что, зная значения функции u(x, t) в точках к – го слоя (t=kl), с помощью этой формулы можно вычислить значения u(x, t) в точках следующего (к+1)-го слоя. Значения функции u(x, t) в точках нулевого слоя задаются равенством (7.22). При вычислении используются граничные узлы, лежащие на прямых х=0, х=b. Значения функции u(x, t) в этих узлах задаются равенствами (7.23). Отметим, что для составления уравнения (7.21) была использована схема узлов, данная на рис. 7.6. Эта схема является явной. Явные схемы позволяют очень просто вычислять значения искомого решения в узлах (к+1)-го слоя по значениям решения в узлах предыдущих слоев.

(i, k+1)

(i-1, k) (i, k) (i+1, k)

Рис. 7.6

Итак, формулы (7.21) –(7.23) позволяют вычислить прибилиженные значения решения в требуемом количестве узлов полуполосы. При этом очень важно знать, насколько близки полученные методом сеток приближенные значения к значениям точного решения смешанной задачи. Естественно, что интерес могут представлять только такие разностные схемы, с помощью которых можно получить приближенное решение, достаточно близкое к точному, так называемые сходящиеся разностные схемы.

Из сходящихся разностных схем практический интерес представляют только те схемы, для которых малые погрешности, допущенные в процессе решения разностных уравнений, не могут привести к большим отклонениям от точного решения системы; они затухают или остаются малыми при неограниченном увеличении номера текущего слоя. Такие схемы называются устойчивыми.

Доказано, что схема (7.21) – (7.23) устойчива при и неустойчива при . Таким образом, на практике шаг вдоль оси 0t выбирается таким, чтобы . При применении метода сеток дифференциальное уравнение (7.16) заменяется конечно – разностным (7.21).

Выясним, чему равна погрешность такой замены. Используя формулу Тейлора, значения функции ; ; запишем в виде

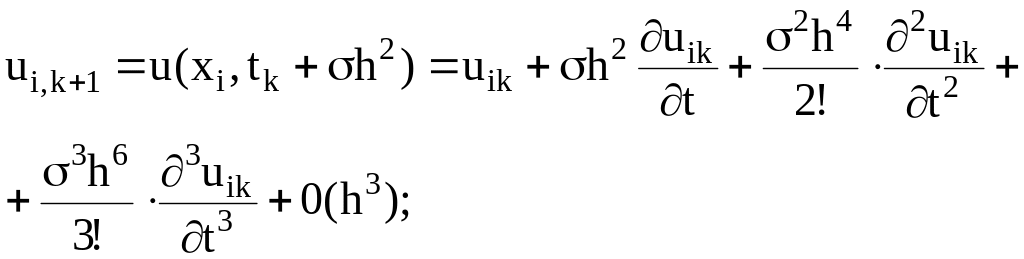(7.24)

.

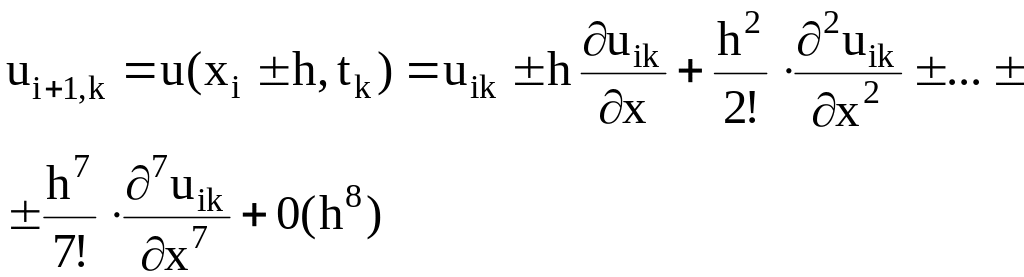Обозначим

.

Подставляя (7.24) в , получим

.

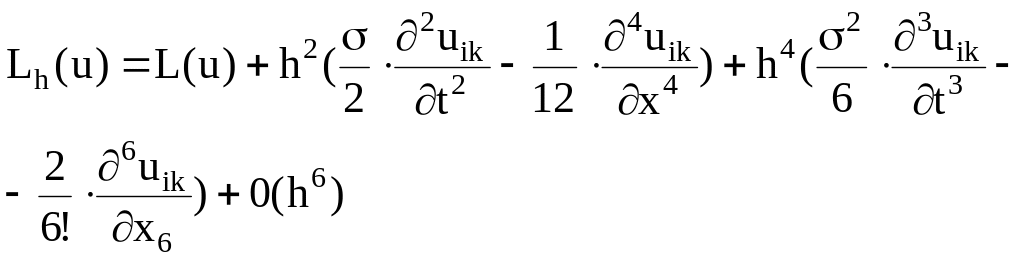Так как u(x, t) – решение уравнения (7.16), имеют место равенства

.

Следовательно

(7.25)

Выберем число таким, чтобы первая скобка формулы (7.25) обратилась в нуль, т.е.

.

Отсюда

.

Таким образом, при погрешность замены дифференциального уравнения конечно – разностным уравнением имеет порядок h⁴. При любом другом выборе погрешность замены имеет порядок h². Формулы (7.21) при записываются в виде

. (7.26)

Рассмотренная явная схема (7.21) является одной из при меняемых на практике разностных схем. Приведем пример другой разностной схемы.

Если, например, производную в дифференциальном уравнении (7.16) заменить левой разностью

,

то для внутреннего узла получим следующее конечно – разностное уравнение:

.

Обозначив , получим

(7.27)

Для составления уравнения (7.27) используется схема узлов, данная на рис. 7.7.

(i-1,k) (i,k) (i+1,k)

(i,k-1)

Рис. 7.7

Эта схема является неявной.

При решении смешанной задачи при помощи неявной схемы необходимо решать систему алгебраических уравнений. В этом ее недостаток по сравнению с явной схемой. В то же время неявная разностная схема (7.27) имеет преимущество перед явной схемой (7.21): схема устойчива при любом .

7.7. Метод сеток для уравнений

гиперболического типа

Рассмотрим смешанную задачу для уравнения колебания струны, заключающуюся в следующем.

Требуется найти решение уравнения

, (7.28)

удовлетворяющее начальным условиям

(7.29)

и граничным условиям

;

. (7.30)

В уравнении (7.28) можно положить а=1, а уравнение (7.28) записать в виде

.

(К виду (7.31) можно прийти введением переменной в уравнение (7.28)).

Решаем смешанную задачу методом сеток. Строим в полуполосе t>0 два семейства параллельных прямых:

шаг вдоль оси 0х);

шаг вдоль оси 0t).

Узлы, лежащие на прямых x=0, x=b, t=0, назовем граничными, остальные узлы считаем внутренними. Рассмотрим дифференциальное уравнение (7.31) во внутреннем узле (х_i, t_k). Заменяя производные разностными отношениями, получим разностное уравнение

. (7.32)

Обозначим . Тогда уравнение (7.32) запишется в виде

. (7.33)

Для составления уравнения (7.33) была использована схема узлов, данная на рис.7.8.

(i, k+1)

h

l

(i-1, k) (i, k) (i+1, k)

(i, k-1)

Рис. 7.8

Полученная разностная схема является явной схемой. Из уравнения (7.33) видно, что для получения значений u(x,t) в (к+1) –м слое необходимы значения u(x,t) в двух предыдущих слоях.

Значения функции u(x,t) на нулевом слое (к=0) задаются первым начальным условием (7.29):

т.е.

. (7.34)

Значения функции u(x,t) на первом слое (к=1) можно приближенно найти из второго начального условия (7.29):

.

Заменяя разностным отношением

,

получаем

(7.35)

Значения функции u(x,t) на прямых х=0 и х=b можно вычислить, используя граничные условия (7.30):

,

. (к=0, 1, 2, 3, …) (7.36)

Таким образом, используя (7.34) – (7.36), по формуле (7.33) можно вычислить значения функции u(x,t) на любом слое.

При решении смешанной задачи методом сеток дифференциальное уравнение (7.31) во внутреннем узле заменяется конечно – разностным (7.33). Аналогично тому, как это делалось для дифференциальных уравнений эллиптического типа, можно показать, что погрешность такой замены имеет порядок h². Погрешность аппроксимации второго начального условия (7.35) имеет порядок h.

Доказано, что разностная схема (7.33) устойчива при . Таким образом, при решении смешанной задачи методом сеток следует сетку строить так, чтобы выполнялось неравенство

.

Итак, рассмотрена простейшая разностная схема. Разработано большое количество разностных схем, аппроксимирующих дифференциальное уравнение (7.28) с различной точностью.