Рассмотрим систему линейных алгебраических уравнений

, (4.28)

где

; ; .

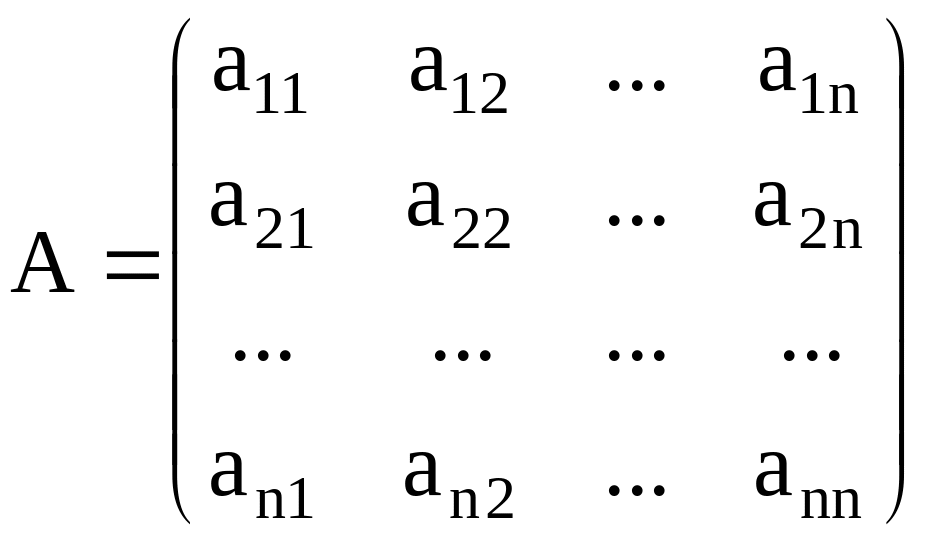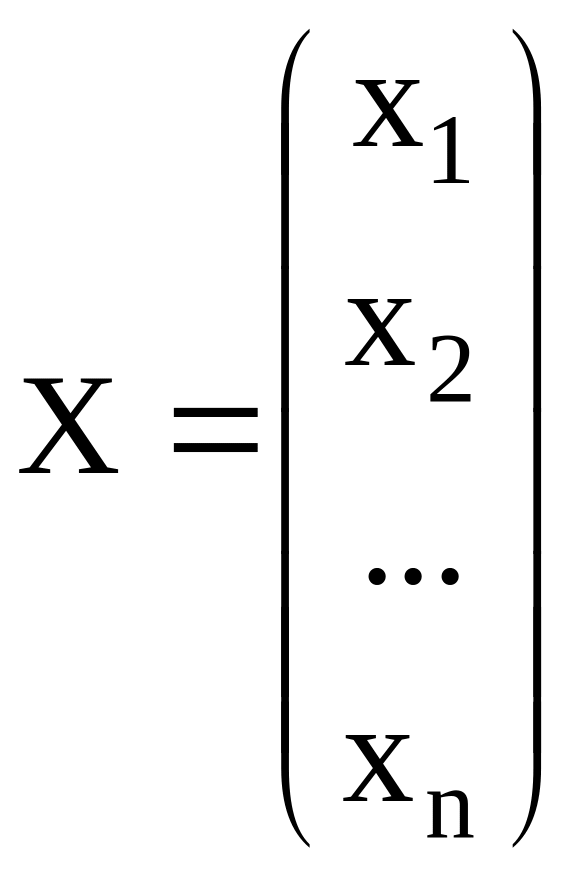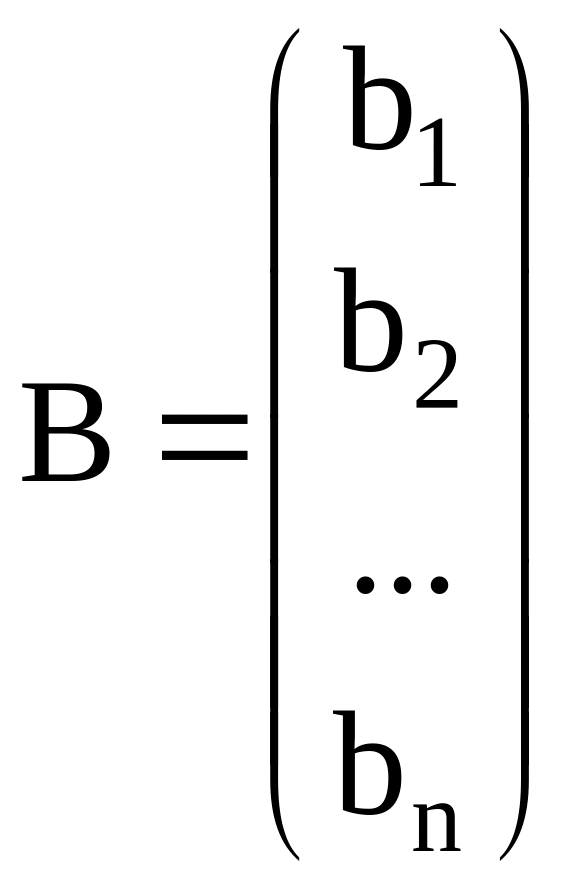Приведем систему (4.28) к виду

, (4.29)

где

; .

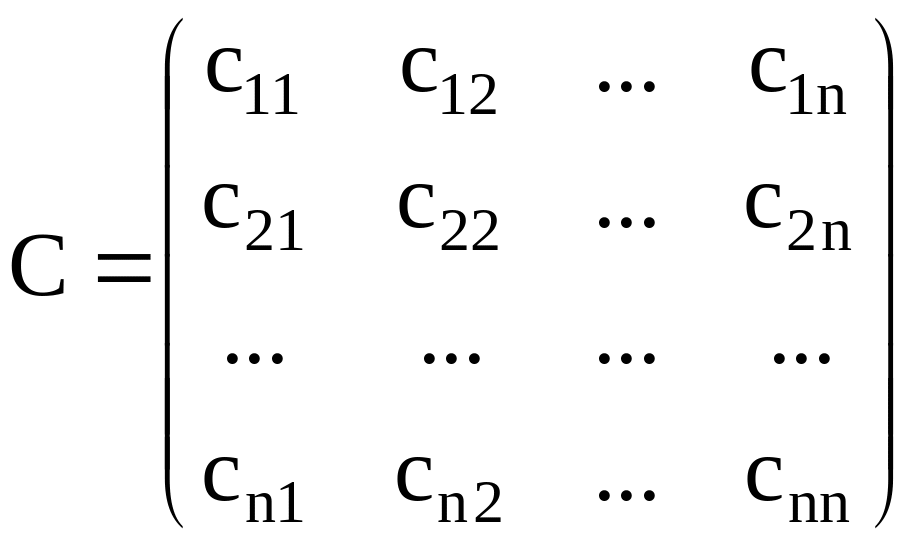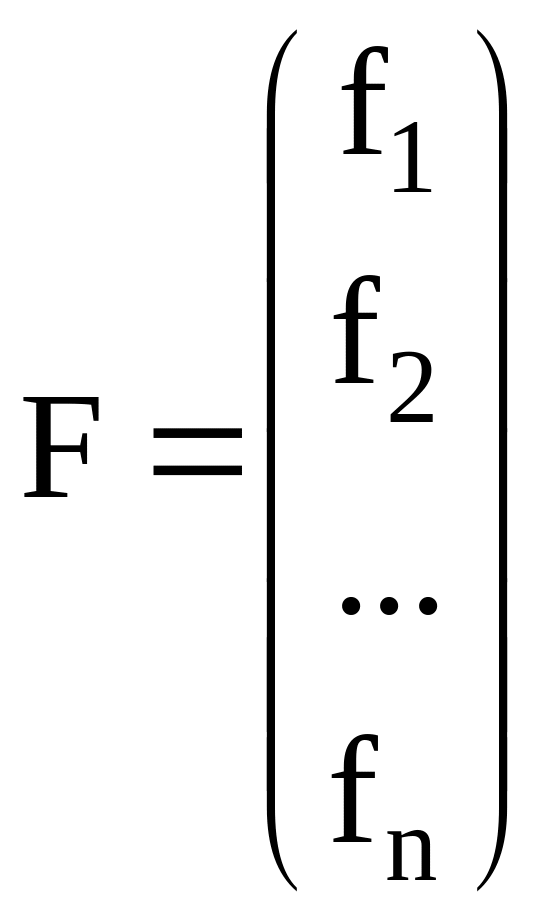В качестве нулевого приближения возьмем произвольный вектор Х₀. Далее строим векторы

; .

И т.д., т.е.

(4.30)

Рассмотрим последовательность векторов . Пусть эта последовательность сходится к вектору Х, т.е.

.

Переходя к пределу при в равенстве (4.30), получаем

.

Таким образом, если последовательность имеет предел, то этот предел является решением системы (4.29). Выясним условия сходимости последовательности Х^(k).

Теорема (достаточное условие сходимости метода простой итерации). Если какая-либо норма матрицы С меньше единицы, то система уравнений (4.29) имеет единственное решение и итерационный процесс (4.30) сходится к решению этой системы.

Доказательство. Рассматриваем систему уравнений X=CX+F. По условию теоремы .

Для всякого решения системы имеем

Отсюда

(4.31)

Пусть вектор F – нулевой вектор. Тогда . Так как норма вектора не может быть отрицательным числом, из (4.31) вытекает, что . Таким образом, однородная система X=CX имеет единственное решение Х=0. А это означает, что определитель системы отличен от нуля, т.е.

Отсюда, в свою очередь, вытекает, что система (4.29) при любом векторе F имеет решение, притом единственное. Пусть Х – решение системы (4.29), а X^(k) – вектор последовательности (4.30):

X=CX+F;

X^(k)=CX^(k-1)+F.

Вычитая второе равенство из первого, получаем

X-X^(k)=C(X-X^(k-1)). (4.32)

Обозначим X-X^(k)=R^(k). Тогда (4.32) можно записать в виде

R^(k)=CR^(k-1):

при k=1 имеем R⁽¹⁾=CR⁽⁰⁾;

при k=2 имеем R⁽²⁾=CR⁽¹⁾=C²R⁽⁰⁾;

при k=3 имеем R⁽³⁾=CR⁽²⁾=C³R⁽⁰⁾.

Продолжая этот процесс, получаем

R^(k)=C^kR⁽⁰⁾. (4.33)

Из определения нормы матрицы вытекает, что

Воспользовавшись этим неравенством и условием согласованности норм матрицы и вектора, получаем из (4.33)

(4.34)

Правая часть неравенства (4.34) стремится к нулю при так как . Отсюда следует, что

при ,

т.е. последовательность X^(k) (4.30) сходится к решению системы Х.

Теорема доказана.

Следствие. Для того, чтобы метод простой итерации для системы уравнений X=CX+F сходился, достаточно, чтобы выполнялось одно из условий:

1) ;

2) (4.35)

3) .

Это следствие вытекает из теоремы и формул (4.24), (4ю25), (4.27). На практике обычно используется первое или второе условие.

Метод простой итерации имеет ряд преимуществ по сравнению с методом Гаусса.

1. Если итерационный процесс сходится достаточно быстро, т.е. если для решения системы требуется менее n итераций, то получаем выигрыш во времени, так как число арифметических действий, необходимых для одной итерации, пропорционально n², а общее число арифметических действий в методе Гаусса пропорционально n³.

2. Погрешность округления в методе итераций сказываются значительно меньше, чем в методе Гаусса. Кроме того, метод итерации является самоисправляющимся.

3. Метод итерации приводит к выполнению однообразных операций и легко програмируется для вычисления на ЭВМ.